Построить сетевую модель и рассчитать все его параметры

1.3.5. Пример построения и расчета сетевой модели

Исходные данные варианта лабораторной работы включают название и продолжительность каждой работы (табл. 1.1), а также описание упорядочения работ.

1. Работы C, I, Gявляются исходными работами проекта, которые могут выполняться одновременно.
2. Работы E иAследуют за работойC.
3. Работа Hследует за работойI.
4. Работы D иJследуют за работойG.
5. Работа Bследует за работойE.
6. Работа Kследует за работамиAиD, но не может начаться прежде, чем не завершится работаH.
7. Работа Fследует за работойJ.

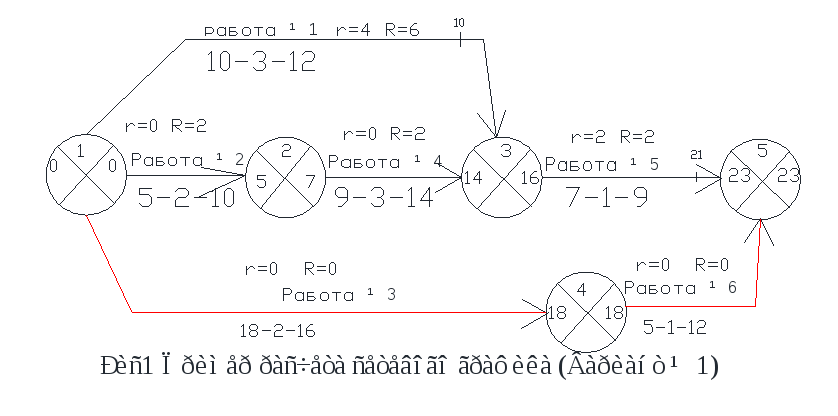
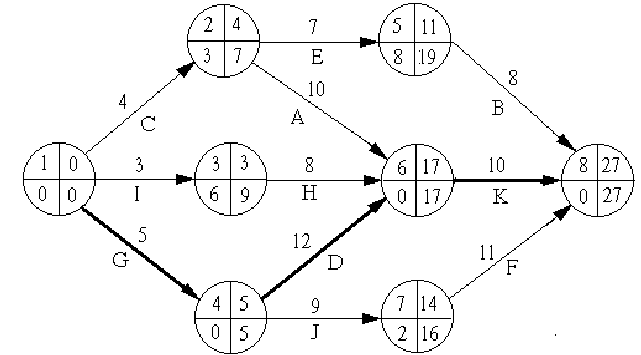
На рис.1.4 представлена сетевая модель, соответствующая данному упорядочению работ. Каждому событию присвоен номер, что позволяет в дальнейшем использовать не названия работ, а их коды (см. табл. 1.2). Численные значения временных параметров событий сети вписаны в соответствующие секторы вершин сетевого графика, а временные параметры работ сети представлены в табл. 1.3. Таблица 1.2 Описание сетевой модели с помощью кодирования работ

Номера событий		Код работы	Продолжительность
начального	конечного	работы
1	2	(1,2)	4
1	3	(1,3)	3
1	4	(1,4)	5
2	5	(2,5)	7
2	6	(2,6)	10
3	6	(3,6)	8
4	6	(4,6)	12
4	7	(4,7)	9
5	8	(5,8)	8
6	8	(6,8)	10
7	8	(7,8)	11

Рис.1.4. Сетевая модель Таблица 1.3 Временные параметры работ

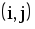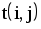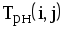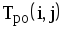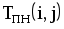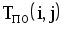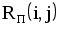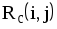1,2	4	0	4	3	7	3	0
1,3	3	0	3	6	9	6	0
1,4	5	0	5	0	5	0	0
2,5	7	4	11	12	19	8	0
2,6	10	4	14	7	17	3	3
3,6	8	3	11	9	17	6	6
4,6	12	5	17	5	17	0	0
4,7	9	5	14	7	16	2	0
5,8	8	11	19	19	27	8	8
6,8	10	17	27	17	27	0	0
7,8	11	14	25	16	27	2	2

1.4. Контрольные вопросы

1.4.1. Зачетный минимум

1. Определение события, виды событий, практические примеры событий, обозначение событий на графике, временные параметры событий.
2. Определение работы, классификация работ с приведением соответствующих практических примеров, обозначение работ на графике, временные параметры работ.
3. Правила построения сетевых графиков.
4. Определение пути в сетевом графике, виды путей, важность определения критического пути.
5. Умение вычислять временные параметры событий и работ.

1.4.2. Дополнительные вопросы

1. Почему при расчете раннего срока свершения события iвыбираютмаксимальнуюиз сумм ?
2. Почему при расчете позднего срока свершения события iвыбираютминимальнуюиз разностей ?
3. Какова взаимосвязь полного и свободного резервов работы?
4. Как можно найти критических путь в сетевой модели, без непосредственного суммирования длительностей работ?

Часть 2. ОПТИМИЗАЦИЯ СЕТЕВЫХ МОДЕЛЕЙ ПО КРИТЕРИЮ «МИНИМУМ ИСПОЛНИТЕЛЕЙ» 2.1. ЦЕЛЬ РАБОТЫ Знакомство с методикой и приобретение навыков проведения оптимизации сетевых моделей по критерию «Минимум исполнителей». 2.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Согласно номеру своего варианта получите данные о количество исполнителей, занятых на каждой работе сетевой модели, и ограничение по численности Nодновременно занятых в работе исполнителей. 2. Постройте в отчете графики привязки и загрузки, используя нормальные длительности работ сети — 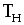(см. п.2.3.1), и покажите их преподавателю. 3. Проверьте правильность построения графиков привязки и загрузки с помощью компьютера, в случае необходимости выявите и устраните ошибки. 4. Используя компьютерную программу, проведите уменьшение численности исполнителей, одновременно занятых на работах сети, до требуемого уровня N. 5. Отчет по лабораторной работе должен содержать:

• номер варианта;
• исходные данные варианта;
• графики привязки и загрузки до проведения оптимизации загрузки;
• графики привязки и загрузки после проведения оптимизации загрузки (возможно использование пунктирных линий на первоначально построенных графиках для отображение изменений в привязке работ и загрузке сети, вызванных сдвигами работ);
• коды работ, сдвинутых в процессе оптимизации, и время их сдвига.

Источник

8.4.2 Построение сетевых моделей и расчет их основных параметров

Построение сетевой модели предусматривает выполнение следующих четырех этапов:

определение целей и ограничений проекта. Цели и ограничения проекта обычно связаны с тремя сторонами реализации проекта (продолжительностью, стоимостью и качеством), а также наличием производственных ресурсов и другими особыми моментами;

определение перечня (совокупности) работ, входящих в проект, и оценку (прогнозирование, расчет) длительности каждой работы (операции);

установление и анализ отношений очередности работ и формирование сетевого графа, отражающего эти отношения;

построение календарного сетевого графика на основе полученного сетевого графа, оценок продолжительности работ, расчета временных параметров и привязки сетевого графика к календарю.

Экономико-математическая модель задачи СПУ имеет следующий вид:

1. Условные обозначения (исходные данные):

h, i, j, k, m— номера событий СГ;

i— номер начального события данной работы,i=1,2. m-1;

j— номер конечного события данной работы,j=2,3. m;

m— номер завершающего события СГ;

h-i— работа, непосредственно предшествующая данной (i-j)-й работе;

j-k— работа, непосредственно следующая за данной (i-j)-й работой;

T_ij — трудоемкость (длительность) выполнения данной работы;

P_ij— потребность в ресурсе для выполнения данной работы;

S— располагаемый фонд ресурсаs-го вида;

P_ijs— количество единиц ресурсаs-го вида, необходимого для выполнения (i-j)-й работы;

T_k—k-й момент времени;

T_нач.ij, T_ок.ij— момент времени соответственно начала и окончания данной (i-j)-й работы;

P_ijsk— количество единиц ресурсаs-го вида, необходимого для выполнения (i-j)-й работы вk-й момент времени (еслиT_нач.ijT_kT_ок.ij, тоk P_ijsk=P_ijs);

S_k— располагаемый вk-й момент времени фонд ресурсаs-го вида;

S_ост.k— остаток фонда ресурсаs-го вида, располагаемого вk-й момент времени;

A> — множество работ СГ, ожидающих выполнения;

A_k> — множество работ СГ, ожидающих выполнения вk-й момент времени;

B_y> — совокупность работ, принадлежащих множеству работ A_k>;

T РН _ij,T РО _ij— моменты времени самого раннего начала и окончания данной (i-j)-й работы соответственно;

T ПН _ij,T ПО _ij— моменты времени самого позднего начала и окончания данной (i-j)-й работы соответственно;

T_кр.— длина критического пути СГ;

r 1 _ij,r 2 _ij— частный резерв времени данной (i-j)-й работы соответственно первого и второго вида;

R_ij— полный (общий) резерв времени данной (i-j)-й работы;

— независимый (свободный) резерв времени (i-j)-й работы;

T— продолжительность выполнения всего комплекса работ данного сетевого графика;

T_дир. — директивный срок выполнения всего комплекса работ данного сетевого графика.

Пример исходных данных (о составе, взаимосвязи и трудоемкости работ некоторого комплекса) для расчета временных параметров сетевого графика и формирования расписания выполнения его работ приведены в таблице 8.7.

Источник

9. Параметры, элементы и правила построения сетевых моделей, расчет сетевого графика (показать на примере).

начала одной или нескольких последующих работ(Рис. 2.3.).

работа, производственный процесс, требующий затрат

Т – к – N рабочего времени, материальных ресурсов, затрат машинного времени.

— — — — — — — — — — — — — Технологическая зависимость — показывает зависимость начала выполнения каких либо последующих работ от окончания одной или нескольких предыдущих.

Позднее окончание работы (а),

Критический путь — это самый длинный путь (в днях) от исходного до завершающего события.

————————————————————————————————

Рис. 2.3. Схема обозначения основных элементов сетевой модели

Правила построения и расчета сетевой модели

1. Направление стрелок следует принимать слева направо
2. Форма модели и графика должна быть простой, без лишних пересечений, большинство работ следует изображать горизонтальными линиями
3. При выполнении параллельных работ, т.е. если одно событие служит началом двух работ или более, заканчивающихся другим событием, вводится зависимость и дополнительное событие, иначе разные работы будут иметь одинаковый код.
4. В графике не должно быть «тупиков», «хвостов» и «циклов». «Тупик» – событие (кроме завершающего), из которого не выходит ни одна работа. «Хвост» – событие (кроме исходного), в которое не входит ни одна работа. «Цикл» – замкнутый контур.
5. Разрабатываемая сетевая модель строительства должна отражать абсолютно достоверно все особенности объекта, для чего предварительно необходимо изучить и проанализировать всю проектно-сметную документацию по объекту.

Сетевая модель и график могут разрабатываться в безразмерном (без масштабном) виде, то есть длина стрелок работ не соответствует значению продолжительности. Прежде чем приступать к расчету необходимо: -сетевую модель строительства объекта согласовать со всеми заинтересованными участниками строительства; -определить продолжительность выполнения каждой работы; -уточнить сроки строительства объекта по договору подряда. Параметры сетевого графика Параметры работ и сетевого графика: -номер события; -продолжительность выполнения работ; -раннее начало и раннее окончание работ; -позднее начало и позднее окончание работ; -частный резерв (запас) времени каждой работы; -общий резерв (запас) времени каждой работы; -длина критического пути (в днях) Расчет сетевого графика До начала выполнения расчета сетевого графика необходимо рассчитать продолжительность выполнения каждой работы сетевого графика. Расчет можно осуществлять графическим (секторным- непосредственно на графике) или табличным способом. Расчет графическим способом начинается с определения ранних сроков начала и окончания работ. Следующий шаг – расчет поздних сроков. Расчет поздних сроков осуществляется, начиная от последнего события. При правильном расчете поздних сроков в первом событии в левом и правом секторе должна быть цифра «0». Путь от первого события до последнего с наибольшим значением продолжительности и носит название «критический путь». Кроме этого следует учитывать то, что критический путь проходит через события, у которых в левом и правом секторе цифры одинаковые, а работы не имеют запасов времени. Критический путь – это самый длинный путь от исходного до завершающего события. Это и есть продолжительность строительства объекта. Работы, лежащие на критическом пути, называются критическими, другие работы являются не критическими и обладают запасами времени – частным и общим. На графиках критический путь выделяется двойной или просто более жирной линией. Возможность определения запасов времени по некритическим работам и использования их при корректировке графиков по различным критериям – это главное отличие и достоинство сетевого моделирования по сравнению с линейными графиками и циклограммами. Следующий шаг — расчет запасов времени – частного и общего. Частный резерв времени ( r) – это количество дней, на которое рассматриваемую работу можно растянуть или передвинуть без изменения ее продолжительности, не изменяя раннее начало последующей работы. Общий резерв времени (R) – это количество дней, на которое рассматриваемую работу можно растянуть или передвинуть без изменения ее продолжительности, не изменяя длины критического пути (продолжительности строительства объекта). Рассчитанный сетевой график приведен на рисунке После завершения расчетов необходимо построить график в масштабе времени и оценить его на предмет соответствия определенным критериям оптимальности.

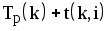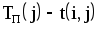Источник