Критический путь
Путь – любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующий за ней работы.
Полный путь L – любой путь, начало которого совпадает с исходным событием сети, а конец – с завершающим.
Наиболее продолжительный полный путь в сетевом графике называется критическим. Критическими также называются работы и события расположенные на этом пути. Работы этого пути определяют общий цикл завершения всего комплекса работ, планируемых при помощи сетевого графика. И для сокращения продолжительности проекта необходимо в первую очередь сокращать продолжительность работ, лежащих на критическом пути.
- Составить экономическое содержание задачи и перечислить перечень работ.
- Построить сетевой график и определить критический путь.
- Рассчитать параметры сетевого графика и поздние сроки поступления событий, резервы времени.
| Работа (i,j) | Количество предшествующих работ | Продолжительность tij | Ранние сроки: начало tij Р.Н. | Ранние сроки: окончание tij Р.О. | Поздние сроки: начало tij П.Н. | Поздние сроки:окончание tij П.О. | Резервы времени: полный tij П | Резервы времени: свободный tij С.В. | Резервы времени: событий Rj |
| (1,2) | 0 | 3 | 0 | 3 | 1 | 4 | 1 | 0 | 1 |
| (1,3) | 0 | 6 | 0 | 6 | 0 | 6 | 0 | 0 | 0 |
| (1,4) | 0 | 4 | 0 | 4 | 9 | 13 | 9 | 9 | 0 |
| (2,3) | 1 | 2 | 3 | 5 | 4 | 6 | 1 | 1 | 0 |
| (2,5) | 1 | 5 | 3 | 8 | 12 | 17 | 9 | 2 | 7 |
| (3,4) | 2 | 7 | 6 | 13 | 6 | 13 | 0 | 0 | 0 |
| (3,5) | 2 | 4 | 6 | 10 | 13 | 17 | 7 | 0 | 7 |
| (3,6) | 2 | 4 | 6 | 10 | 15 | 19 | 9 | 9 | 0 |
| (4,6) | 2 | 6 | 13 | 19 | 13 | 19 | 0 | 0 | 0 |
| (5,6) | 2 | 2 | 10 | 12 | 17 | 19 | 7 | 7 | 0 |
Критический путь: (1,3)(3,4)(4,6)
Продолжительность критического пути: 19 Перейти к онлайн решению своей задачи Пример . Рассчитать параметры сетевого графика мероприятия по совершенствованию системы управления. Сетевая модель задана таблично. Продолжительность выполнения работ дана в виде минимальной и максимальной оценок. Требуется вычислить табличным методом все основные характеристики работ и событий, найти критический путь и его продолжительность.
Скачать
Этап 3. Расчет параметров сетевой модели графическим методом; определение критического пути и его продолжительности.
- Ранний срок свершения события
;
- Поздний срок свершения события
;
- Резерв времени события
;
- Полный резерв времени события
;
- Свободный резерв времени события
.
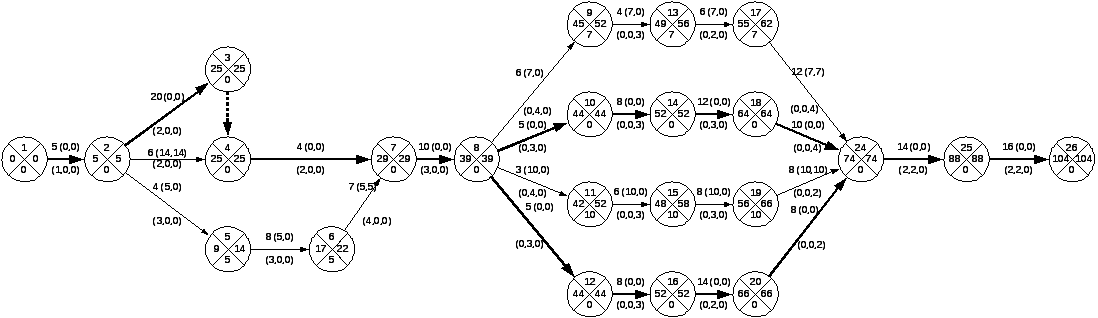
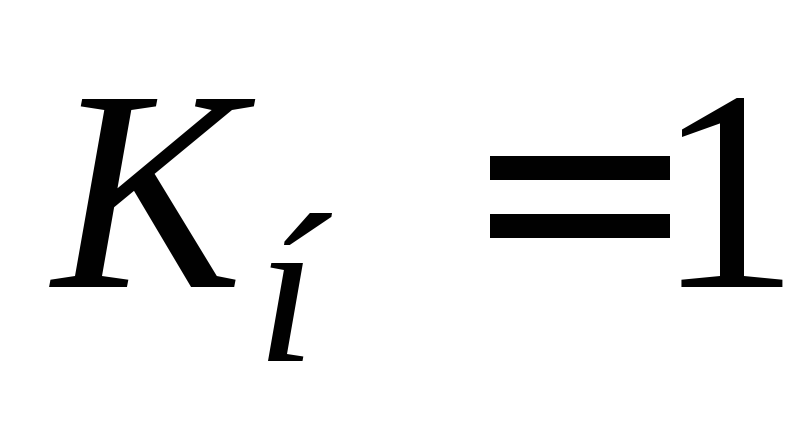
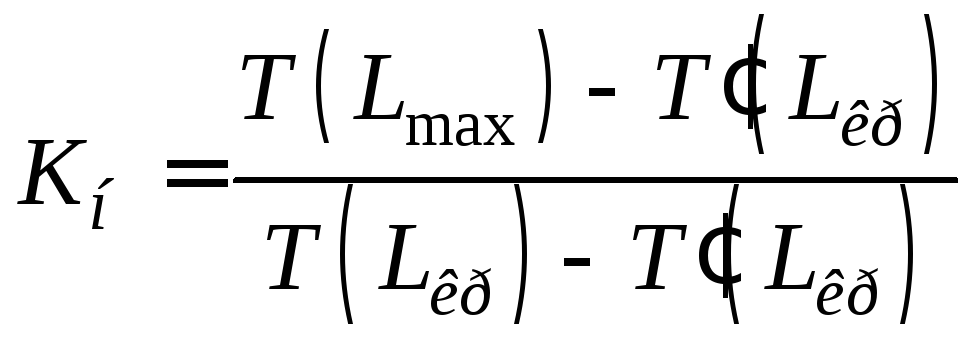
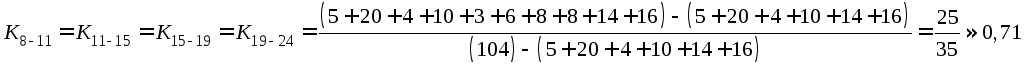
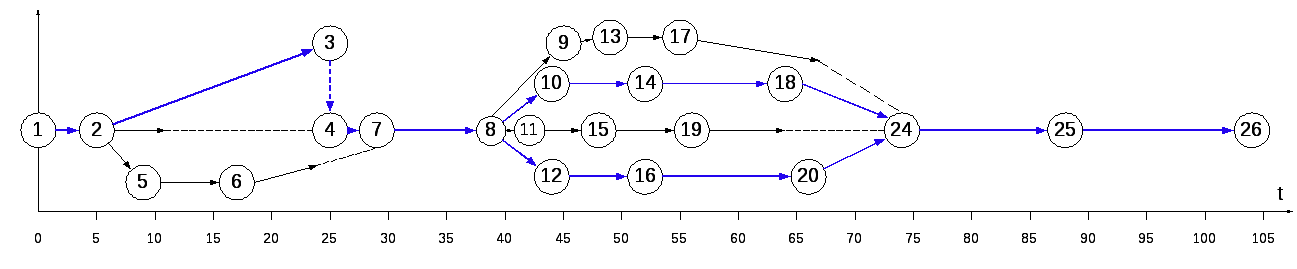
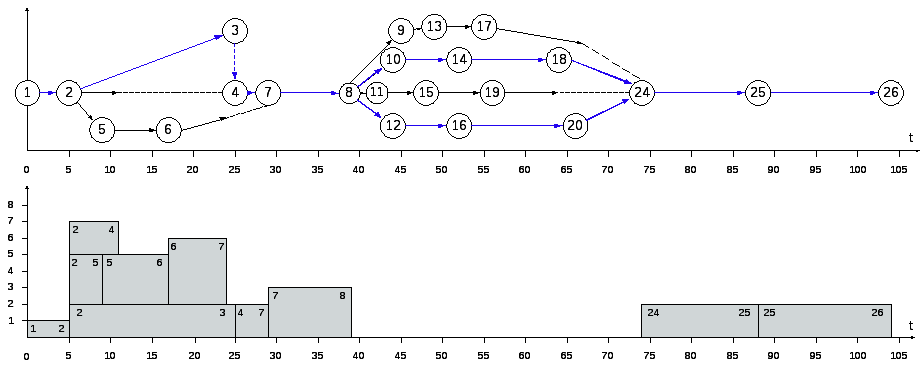
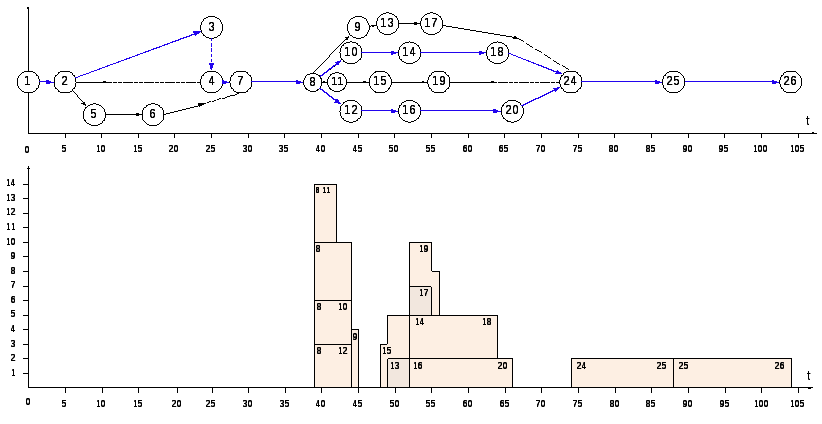
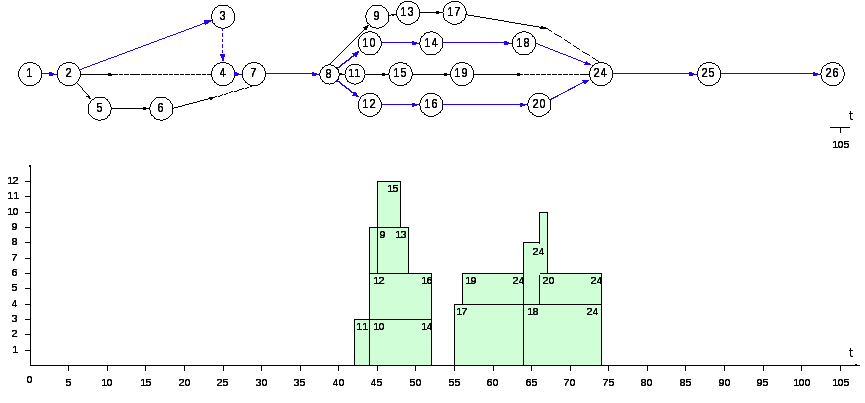
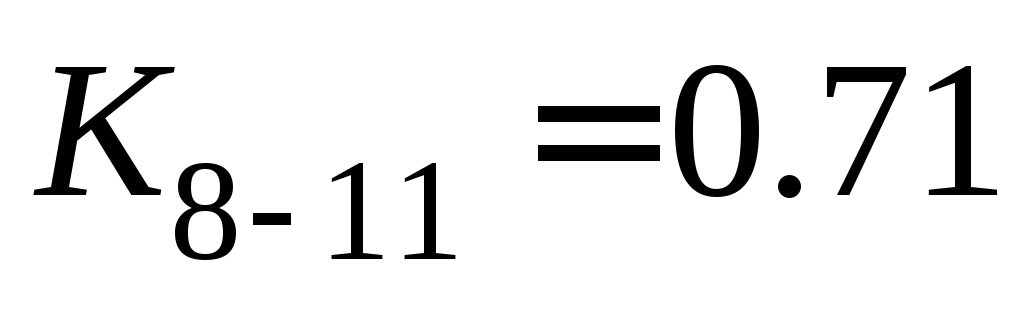
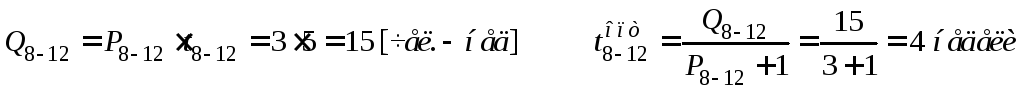
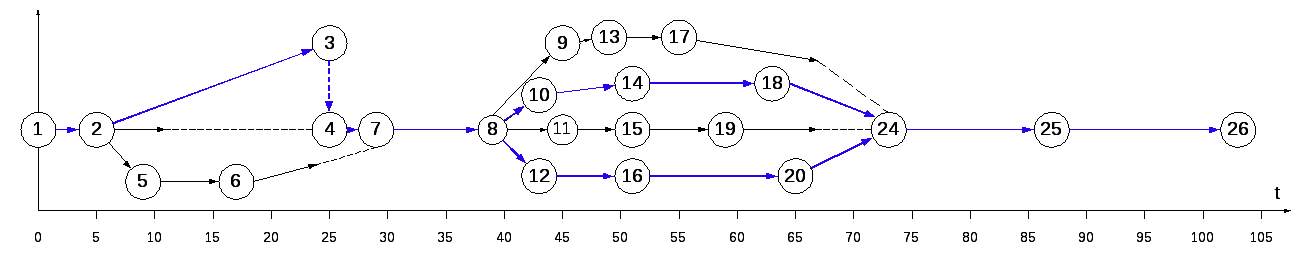
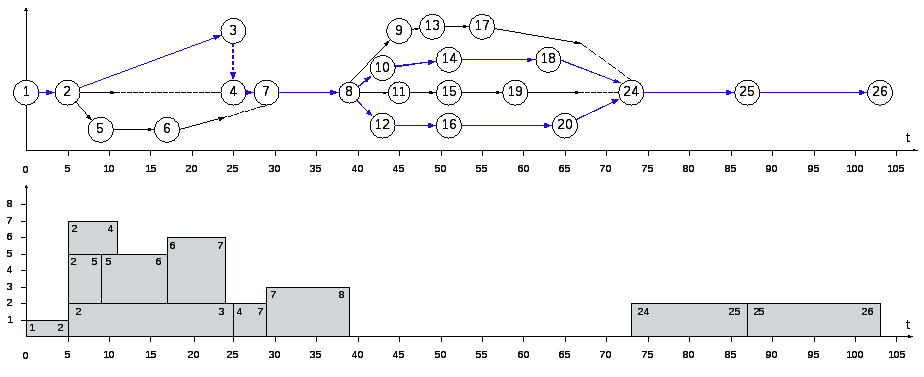
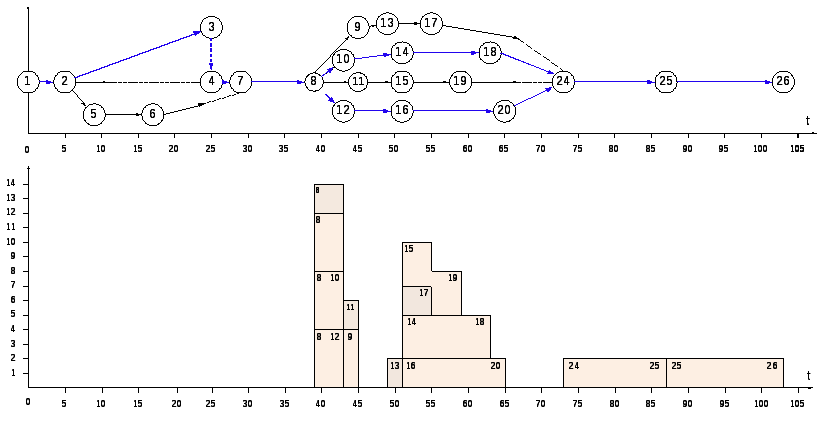
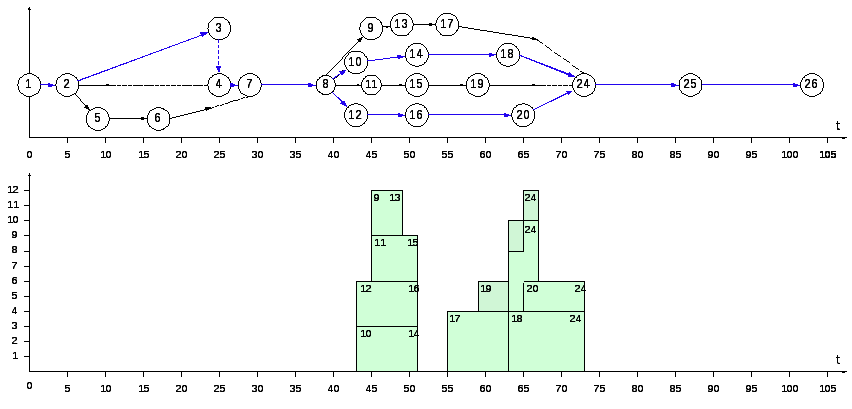
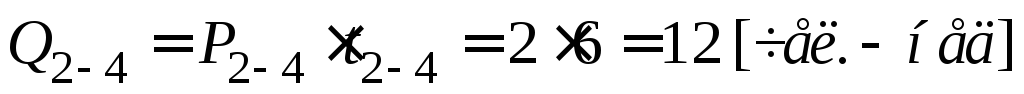
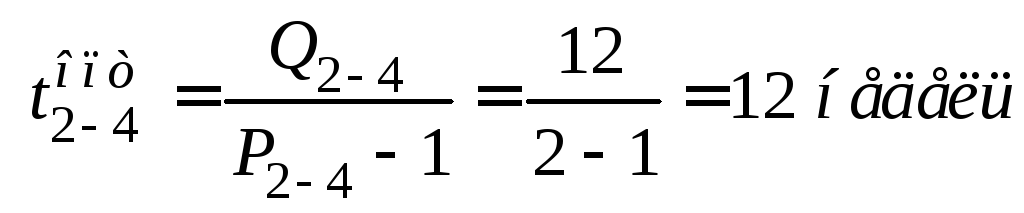
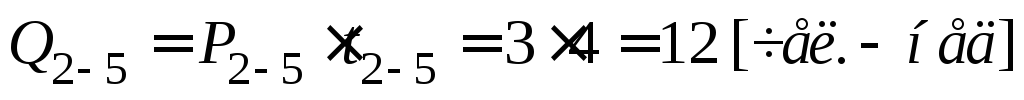
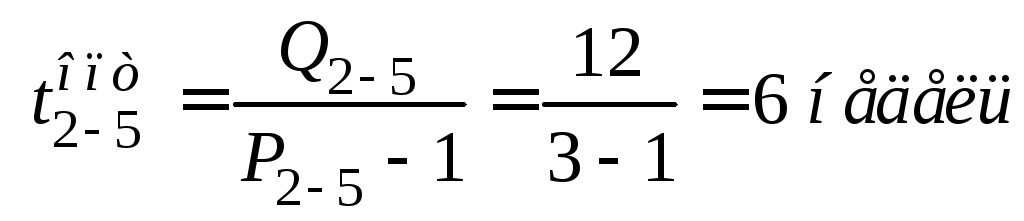
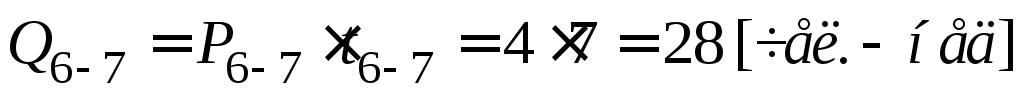
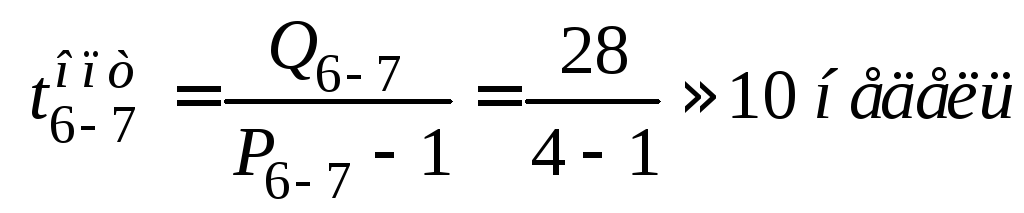
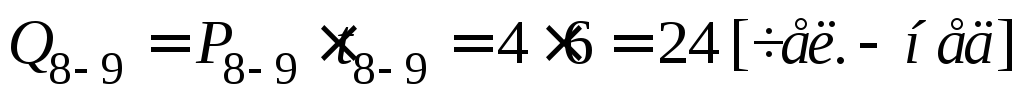
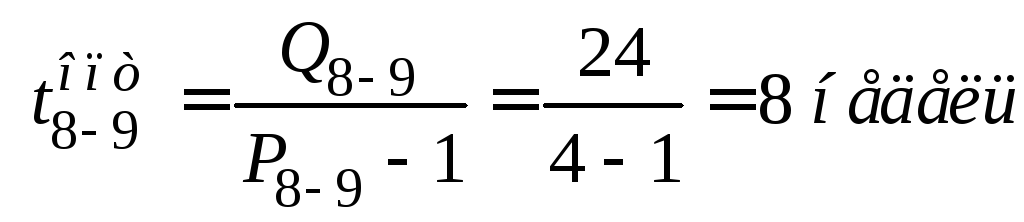
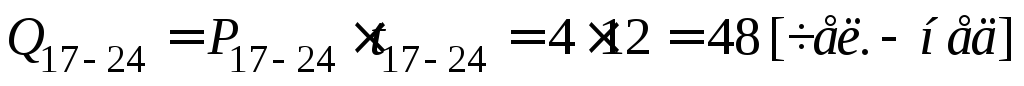
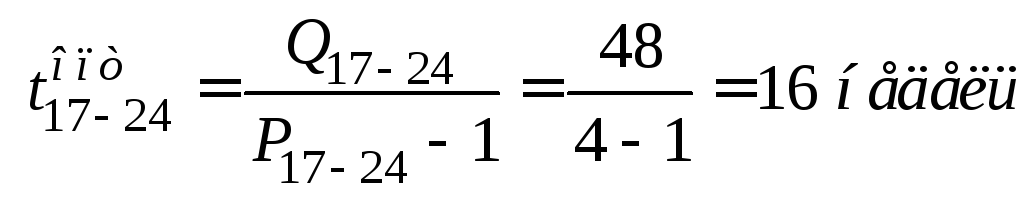
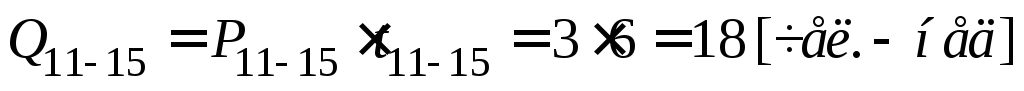
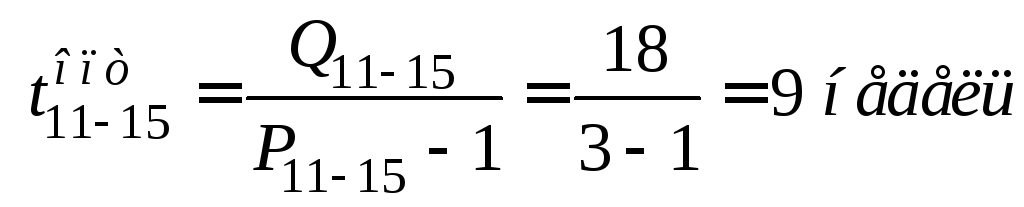
Определение критического пути
Будем предполагать, что время выполнения каждой работы точно известно. Введем следующие определения.
Путь— последовательность взаимосвязанных работ, ведущая из одной вершины проекта в другую вершину. Например (см. Рисунок 48), и – два различных пути.
Рисунок 48. Различные пути на сетевом графике
Длина пути— суммарная продолжительность выполнения всех работ пути.
Полный путь— это путь от исходного к завершающему событию.
Критический путь— полный путь, суммарная продолжительность выполнения всех работ которого является наибольшей.
Очевидно, что минимальное время, необходимое для выполнения любого проекта равно длине критического пути. Именно на работы, принадлежащие критическому пути, следует обращать особое внимание. Если такая работа будет отложена на некоторое время, то время окончания проекта будет отложено на то же время. Если необходимо сократить время выполнения проекта, то в первую очередь нужно сократить время выполнения хотя бы одной работы на критическом пути.
Для того, чтобы найти критический путь, достаточно перебрать все пути и выбрать тот, или те из них, которые имеют наибольшую суммарную продолжительность выполнения работ. Однако для больших проектов реализация такого подхода связана с вычислительными трудностями. Метод критического пути (метод CPM — Critical Path Method) позволяет получить критический путь намного проще.
Расчет сетевой модели начинают с временных параметров событий, которые вписывают непосредственно в вершины сетевого графика (Рисунок 49):
–ранний срок наступления события i, минимально необходимый для выполнения всех работ, которые предшествуют событию i;
–поздний срок наступления события i, превышение которого вызовет аналогичную задержку наступления завершающего события сети;
–резерв события i, т.е. время, на которое может быть отсрочено наступление события i без нарушения сроков завершения.

- для исходного события S:
;
- для всех остальных событий i:
,
где максимум берется по всем работам (k,i), входящим в событие i; 


- для завершающего события F:
;
- для всех остальных событий i:
,
где минимум берется по всем работам (i,j), выходящим из события i; 

- необходимое условие: нулевые резервы событий, лежащих на критическом пути
;
- достаточное условие: нулевые полные резервы работ, лежащих на критическом пути
.
— показывает максимальное время, на которое можно увеличить длительность работы (i,j) или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом.
Пример Рассмотрим пример. Компания разрабатывает строительный проект. Исходные данные по основным операциям проекта представлены в таблице. Нужно построить сетевую модель проекта, определить критические пути и проанализировать, как влияет на ход выполнения проекта задержка работы D на 4 недели.
| Работа | Непосредственно предшествующая работа | Длительность, недели |
| A | — | 4 |
| B | — | 6 |
| C | A, B | 7 |
| D | B | 3 |
| E | C | 4 |
| F | D | 5 |
| G | E,F | 3 |
Сетевой график проекта показан на рисунке ниже (см. Рисунок 52). 
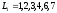


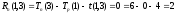


Задачи сетевого планирования
На этой странице вы найдете решенные типовые задания из контрольных по сетевому планированию — разделу экономико-математических методов и моделей.
В рамках изучения сетевого анализа студенты обычно учатся: строить график сети по табличному или словесному описанию проекта (и наоборот), находить ранние и поздние сроки начала и окончания работ, резервы, критический путь и минимальное времеия завершения проекта. Более сложные задания подразумевают различные варианты корректировки и оптимизации сетевого графика (с увеличением времени и уменьшением затрат, или наоборот, с уменьшением времени и увеличением расходов), задачи распределения ресурсов. Изучаются различные графические способы отображения как сетевого графика (см. задачи ниже), так и других диаграмм для проекта (диаграмма Ганта, линейный график).
Примеры решений задач по сетевому планированию онлайн
Задача 1. Для заданной сетевой модели некоторого комплекса работ определить время и критический путь.
Задача 2. Издатель имеет контракт с автором на издание его книги. Ниже представлена последовательность (упрощенная) процессов, приводящая к реализации проекта издания книги. Необходимо разработать сеть для этого проекта.
Задача 3. 1. По заданному перечню работ, построить сетевой график.
2. Определить продолжительности полных путей графика.
3. Определить и выделить критический путь.
4. Определить резерв времени каждого пути.
5. Определить коэффициенты напряженности пути.
6. Определить ранние и поздние сроки начала и окончания работы.
7. Определить полный резерв времени каждой работы.
Задача 4. Рассчитать параметры сетевого графика (см. таблицу работ в файле).
Задача 5. На сетевом графике найти ранние и поздние сроки наступления событий, определить критический путь и резервы времени каждого события.
Задача 6. Построить сетевой график. Решить задачу оптимального распределения ресурсов по работам при постоянных интенсивностях. Наличие ресурса R=10. Работы не допускают перерыва в их выполнении.
Задача 7. По данным варианта требуется:
1) построить сетевую модель;
2) определить критические пути модели;
3) провести максимально возможное уменьшение сроков выполнения проекта при минимально возможных дополнительных затратах

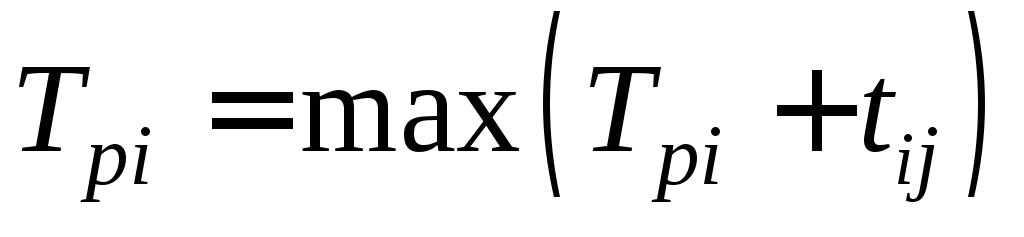 ;
;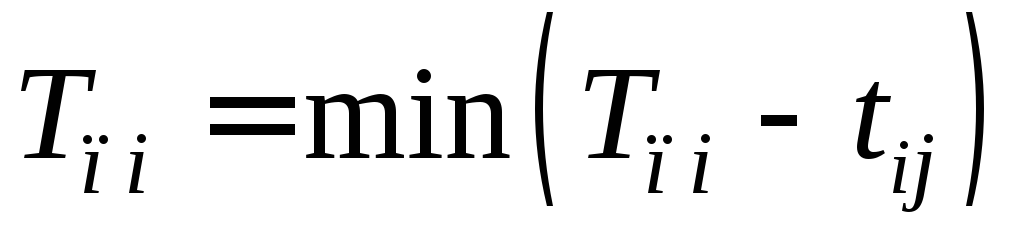 ;
;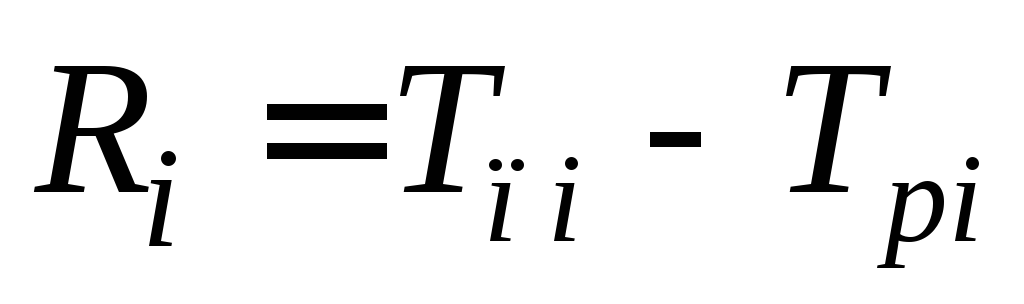 ;
;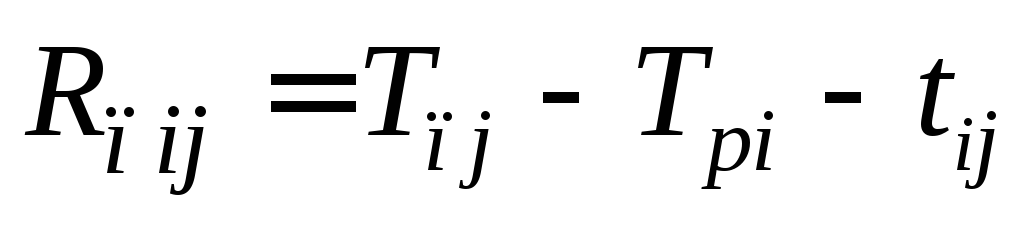 ;
;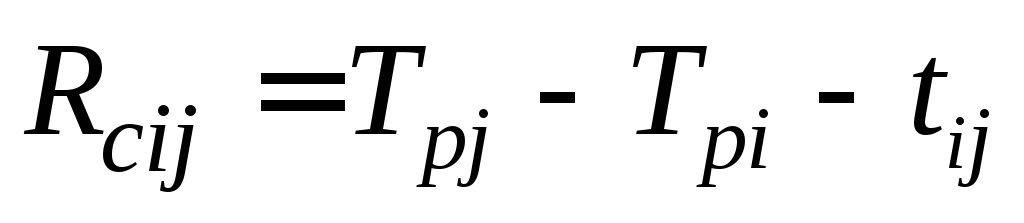 .
.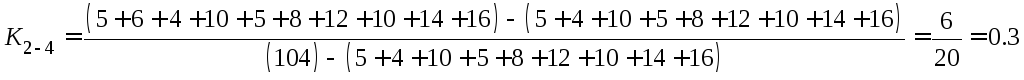

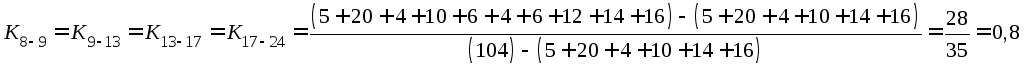
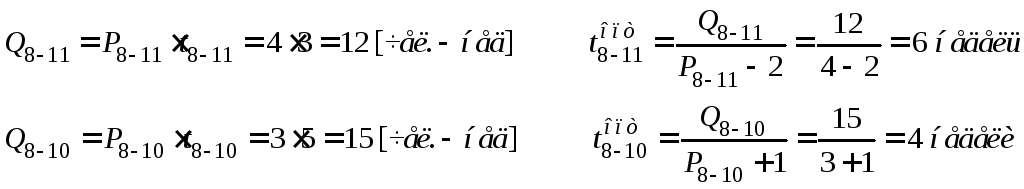

 –ранний срок наступления события i, минимально необходимый для выполнения всех работ, которые предшествуют событию i;
–ранний срок наступления события i, минимально необходимый для выполнения всех работ, которые предшествуют событию i; –поздний срок наступления события i, превышение которого вызовет аналогичную задержку наступления завершающего события сети;
–поздний срок наступления события i, превышение которого вызовет аналогичную задержку наступления завершающего события сети; –резерв события i, т.е. время, на которое может быть отсрочено наступление события i без нарушения сроков завершения.
–резерв события i, т.е. время, на которое может быть отсрочено наступление события i без нарушения сроков завершения. ;
; ,
, ;
; ,
, ;
; .
. — показывает максимальное время, на которое можно увеличить длительность работы (i,j) или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом.
— показывает максимальное время, на которое можно увеличить длительность работы (i,j) или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом.