Примеры решения задач по сетевому планированию
- Модели сетевого планирования и управления
Построить график данного комплекса работ.
Требуется рассчитать:- временные характеристики сетевого графика при нормальном режиме работ;
- найти критический путь;
- полные резервы времени;
- временные характеристики сетевого графика при срочном режиме работ;
- найти критический путь;
- полные резервы времени;
- определить стоимость работ.
- Табличный метод расчета параметров сетевого графика
Определить временные параметры сетевого графика на рисунке, пользуясь табличным методом. - Графический метод расчета параметров сетевого графика
- Расчет параметров сетевого графика методом потенциалов.
- Различные варианты анализа сетевых графиков
Имеются данные о возможности сокращения продолжительности работы за счет стимулирования труда и увеличения других затрат. На основе статистических характеристик проводится анализ сетевой модели. - Оптимизация сетевой модели комплекса производственных работ
- Построение сетевого графика по таблице
Рассчитать параметры сетевого графика мероприятия по совершенствованию системы управления. Сетевая модель задана таблично (Таблица). Продолжительность выполнения работ дана в виде минимальной и максимальной оценок. Требуется:- Вычислить табличным методом все основные характеристики работ и событий, найти критический путь и его продолжительность.
- Построить масштабный сетевой график.
- Оценить вероятность выполнения всего комплекса работ за 30 дней.
- Оценить максимально возможный срок выполнения всего комплекса работ с вероятностью 95%.
- Коэффициент сложности сетевого графика
- Коэффициент напряженности.
- Как решать, если задана стоимость работ?
По данным таблицы необходимо: 1) построить сетевой график; 2) определить критический путь и стоимость проекта при минимально возможных значениях продолжительности всех работ; 3) найти минимальную стоимость проекта при том же сроке его завершения; 4) рассчитать и построить оптимальную зависимость стоимости проекта от продолжительности его выполнения, используя в качестве первоначального варианта сетевого графика.
Правила ввода данных
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus .
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Поиск
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus .
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Сетевая модель задачи и ее решение.
Изобразим моменты i=1,2. N+1 в виде вершин графа, а пары (i,j) в виде ориентированных дуг этого графа (основные понятиятеории графови терминология приведены в Приложении). Проставим на дугах (i,j) соответствующие стоимости арендыCijи будем считать их длинами этих дуг. Тогда произвольный планможно представить как путь из вершины1в вершинуN+1, а стоимость плана – длиной этого пути. Наоборот, каждый путь указанного вида является планом аренды. Оптимальным планом аренды будет кратчайший путь из1вN+1. Таким образом, задача об аренде оборудования является частным случаем известной задачи о нахождении кратчайшего пути (маршрута) [1,2,4].
Полученный граф (сеть) с заданными числами-стоимостями на дугах называется сетевой модельюзадачи об аренде оборудования, а нахождение оптимального плана (оптимальных планов) аренды как кратчайшего пути на этой сети – решением на сетевой модели.
Найдём путь методом потенциалов[2-3, 6] для бесконтурных сетей.
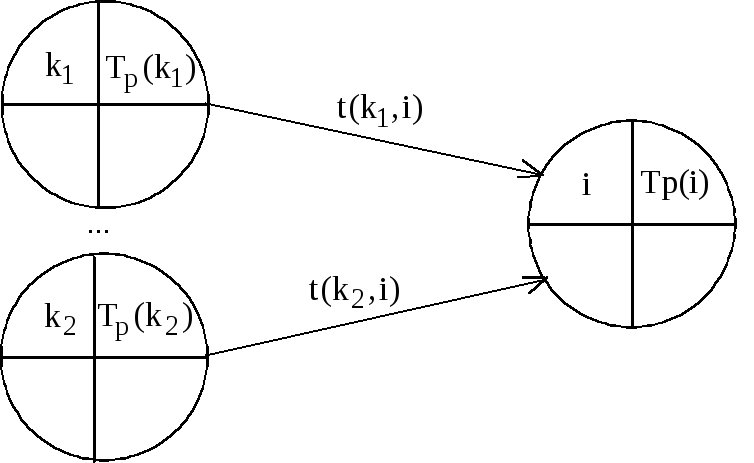
На 1-м этапе находим потенциалы— числаVi для каждой вершиныi, означающие кратчайшие расстояния от вершиныiдо конечной вершиныN+1. Потенциалы найдем, начиная с последней и далее по убыванию номеров вершин по формуле

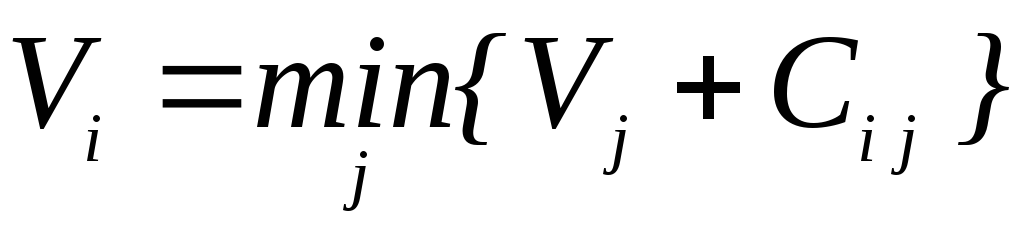
минимум берётся по всем дугам (i,j),выходящимизвершиныi .
На втором этапе, начиная с вершины i=1, находятся и выделяются дуги (i,j), на которых потенциал начала дуги
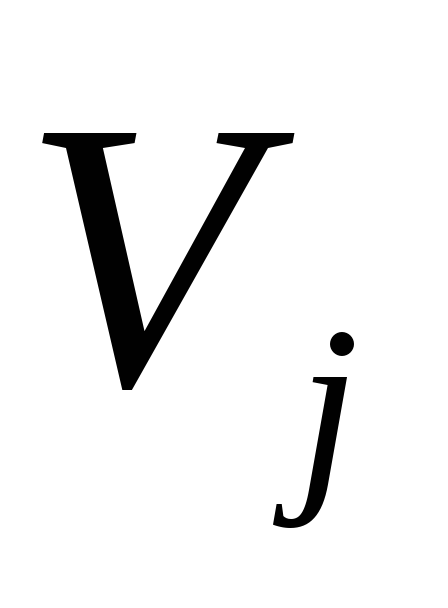

Пример 2. . Пусть при N=6 стоимости аренды Cij заданы в таблице:
j
Задача №7.02
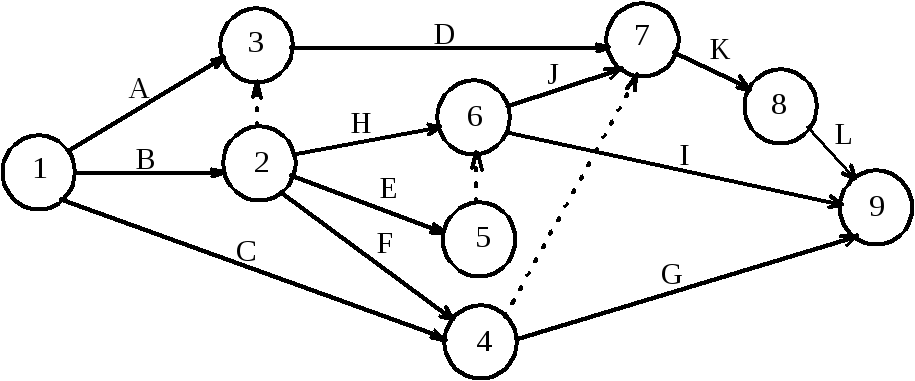
Постройте сетевую модель, включающую работы A, B, C, . L, которая отображает следующее упорядочение работ:
- A, B и C – исходные операции проекта;
- A и B предшествуют D;
- B предшествует E, F и H;
- F и C предшествует G;
- E и H предшествуют I и J;
- C, D, F и J предшествуют K;
- K предшествует L.
Решение
В пункте 1) условия явно указано, что A, B и C являются исходными работами, поэтому изобразим их тремя стрелками, выходящими из исходного события 1. Пункт 2) условия означает, что стрелки работ A и B должны окончиться в одном событии, из которого выйдет стрелка работы D. Но поскольку стрелки работ A и B также и начинаются в одном событии, то имеет место параллельность работ, которая недопустима правилами построения сетевых моделей (см. рис.7.5). 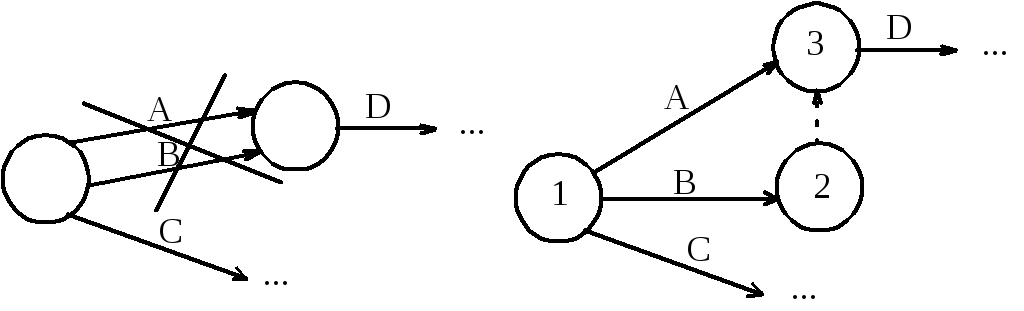
8. Расчет и анализ сетевых моделей
8.1. Теоретическое введение
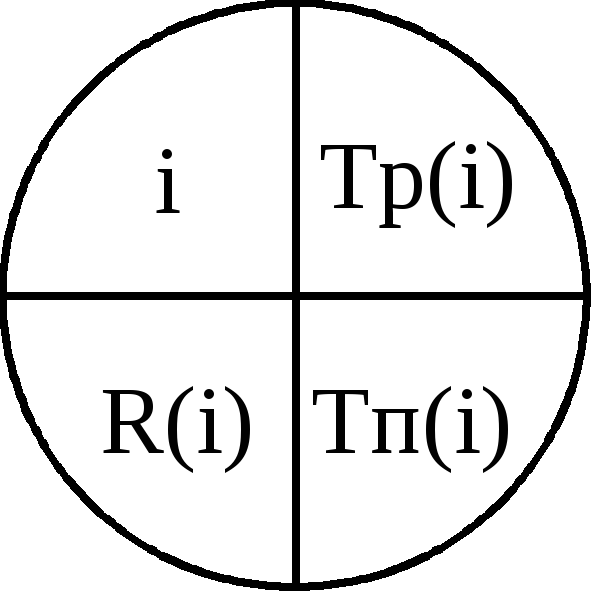
Календарное планирование предусматривает определение моментов начала и окончания каждой работы и других временных характеристик сетевого графика. Это позволяет проанализировать сетевую модель, выявить критические работы, непосредственно определяющие срок выполнения проекта, провести оптимизацию использования ресурсов (временных, финансовых, исполнителей). Расчет сетевой модели начинают с временных параметров событий, которые вписывают непосредственно в вершины сетевого графика(рис.8.1):
–ранний срок наступления события i, минимально необходимый для выполнения всех работ, которые предшествуют событию i;
–поздний срок наступления события i, превышение которого вызовет аналогичную задержку наступления завершающего события сети;
–резерв события i, т.е. время, на которое может быть отсрочено наступление события i без нарушения сроков завершения проекта в целом.
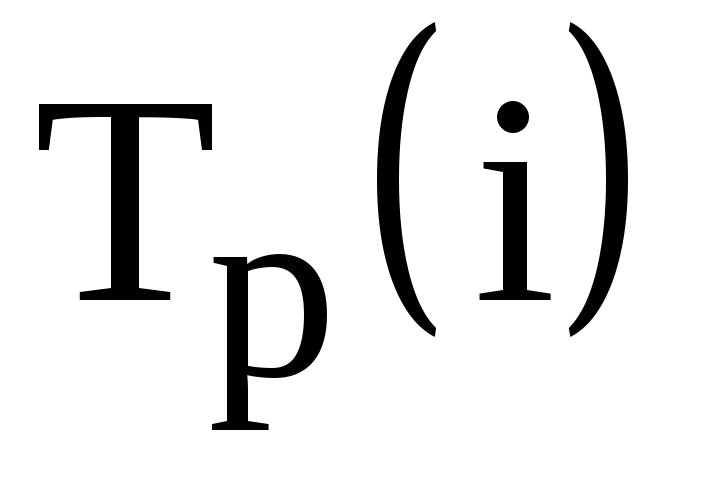
- для исходного события И
;
- для всех остальных событий I

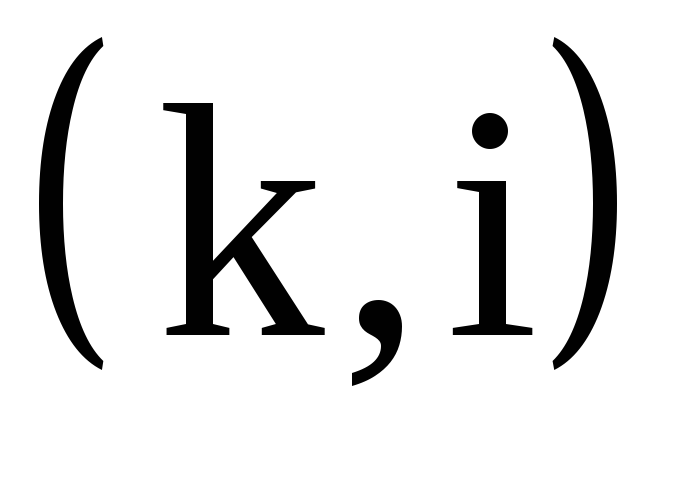
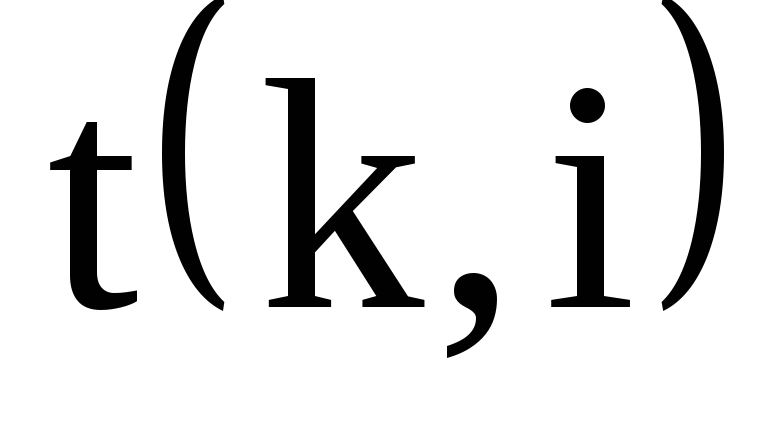


- для завершающего события З
;
- для всех остальных событий
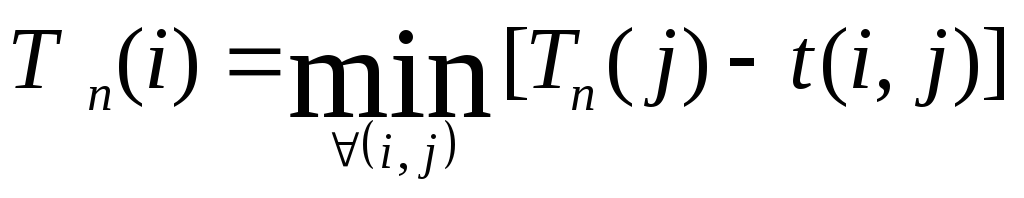
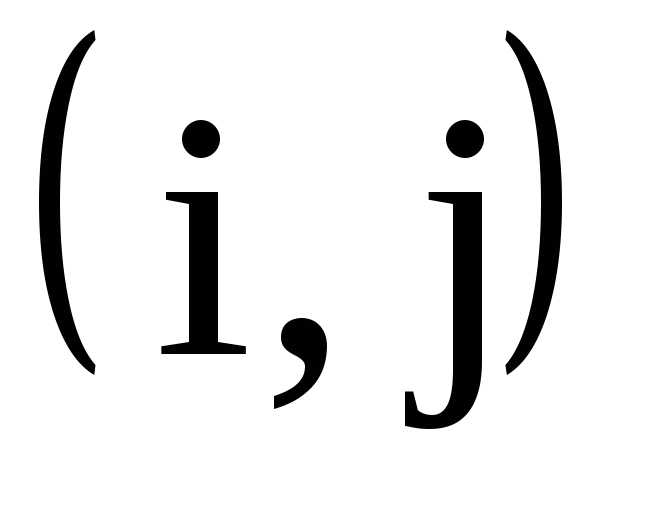


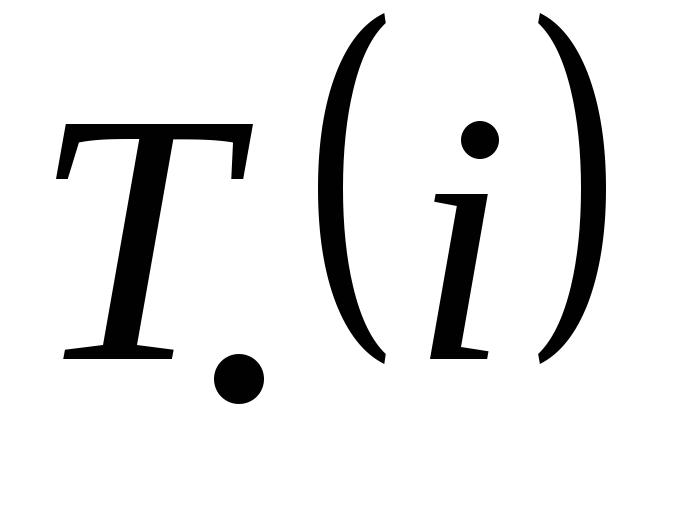
–ранний срок начала работы;
–ранний срок окончания работы;
–поздний срок окончания работы;
–поздний срок начала работы;
–полный резерв работы показывает максимальное время, на которое можно увеличить длительность работы
или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом;
–свободный резерв работы показывает максимальное время, на которое можно увеличить продолжительность работы
или отсрочить ее начало, не меняя ранних сроков начала последующих работ.
Путь – это последовательность работ в сетевом графике (в частном случае это одна работа), в которой конечное событие одной работы совпадает с начальным событием следующей за ней работы. Полный путь – это путь от исходного до завершающего события. Критический путь – максимальный по продолжительности полный путь. Работы, лежащие на критическом пути, называют критическими. Критические работы имеют нулевые свободные и полные резервы. Подкритический путь – полный путь, ближайший по длительности к критическому пути. Для проведения анализа временных параметров сетевой модели используют график привязки, который отображает взаимосвязь выполняемых работ во времени. По вертикальной оси графика привязки откладываются коды работ, по горизонтальной оси – отрезки, соответствующие длительностям работ (раннее начало и раннее окончание работ). График привязки можно построить на основе данных о продолжительности работ. При этом необходимо помнить, что работа 
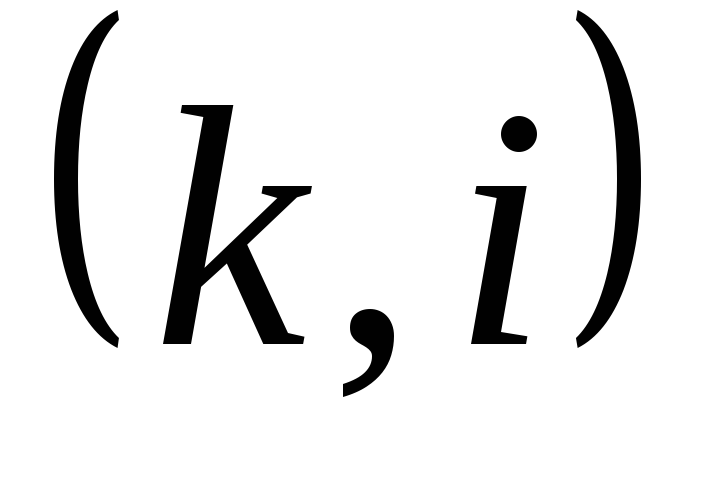
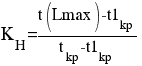

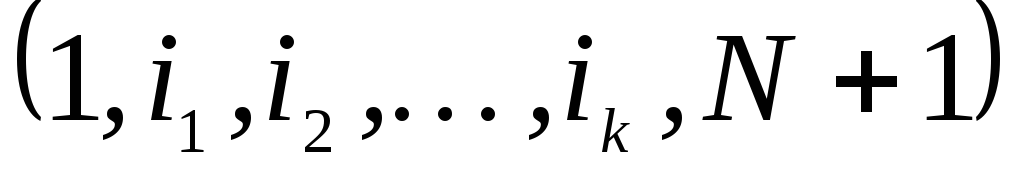


 –ранний срок наступления события i, минимально необходимый для выполнения всех работ, которые предшествуют событию i;
–ранний срок наступления события i, минимально необходимый для выполнения всех работ, которые предшествуют событию i;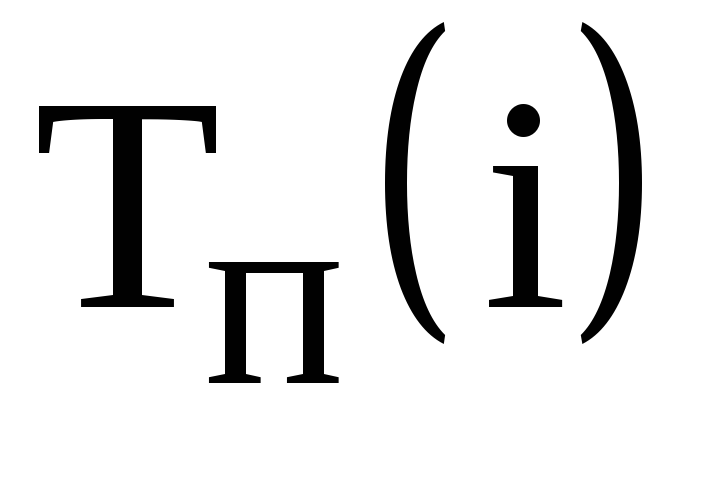 –поздний срок наступления события i, превышение которого вызовет аналогичную задержку наступления завершающего события сети;
–поздний срок наступления события i, превышение которого вызовет аналогичную задержку наступления завершающего события сети;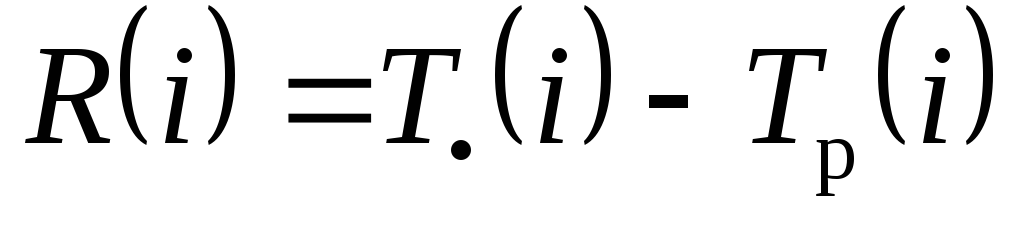 –резерв события i, т.е. время, на которое может быть отсрочено наступление события i без нарушения сроков завершения проекта в целом.
–резерв события i, т.е. время, на которое может быть отсрочено наступление события i без нарушения сроков завершения проекта в целом. ;
;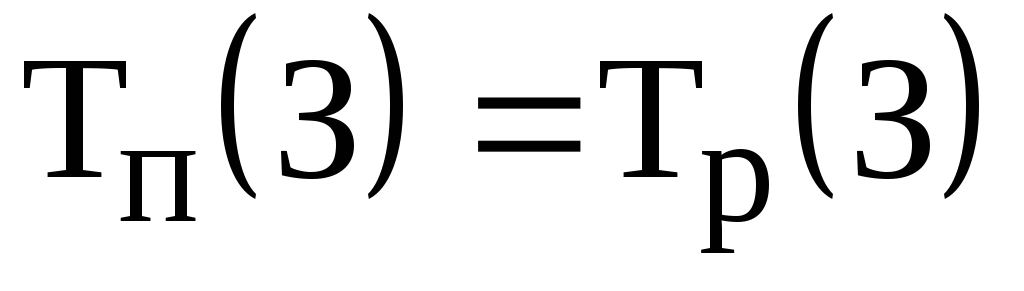 ;
;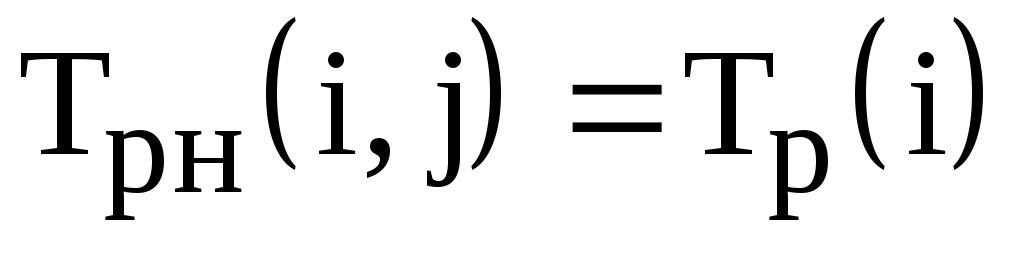 –ранний срок начала работы;
–ранний срок начала работы; –ранний срок окончания работы;
–ранний срок окончания работы; –поздний срок окончания работы;
–поздний срок окончания работы;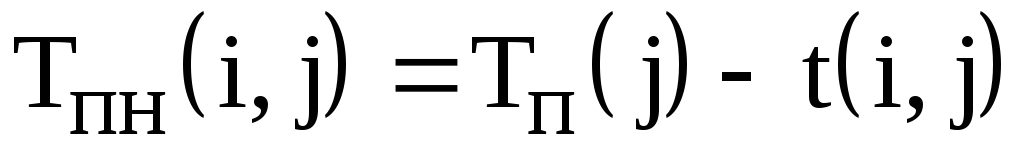 –поздний срок начала работы;
–поздний срок начала работы;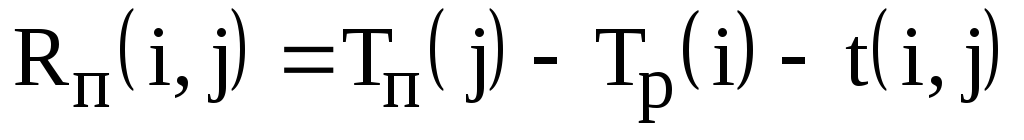 –полный резерв работы показывает максимальное время, на которое можно увеличить длительность работы
–полный резерв работы показывает максимальное время, на которое можно увеличить длительность работы  или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом;
или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом;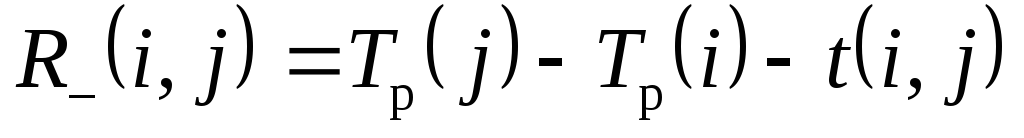 –свободный резерв работы показывает максимальное время, на которое можно увеличить продолжительность работы
–свободный резерв работы показывает максимальное время, на которое можно увеличить продолжительность работы  или отсрочить ее начало, не меняя ранних сроков начала последующих работ.
или отсрочить ее начало, не меняя ранних сроков начала последующих работ.