Построить сетевую модель выполнения комплекса работ

4.2.2. Сетевая модель комплекса работ

Сложные системы, к которым относятся и экономические системы, часто можно представить графом или сетью. Изучение сетевой модели помогает составить достаточно ясное представление о системе и ее функционировании. В сетевом планировании приводятся методы наглядной записи всей информации о планируемом комплексе работ, методы, позволяющие вычислять время, необходимое для выполнения всех работ проекта (критическое время), и указать последовательность работ (критический путь), выполнение которых предопределяет критическое время проекта, а также методы вычисления других важных характеристик проекта.

Задачи рационального планирования сложного комплекса работ имеют следующие общие черты:

• весь комплекс работ представляет собой совокупность более мелких звеньев, элементарных работ;
• работы друг друга обусловливают, то есть не могут выполняться в произвольном порядке, для начала одних работ требуется предварительное выполнение некоторых других.

Решение этих задач методами сетевого планирования предполагает построение сетевой модели комплекса работ. Сетевая модель изображается в виде сетевого графика, отображающего технологическую взаимосвязь между работами. В сетевом планировании основные элементы сетевого графика (дуги и вершины) принято называть работами и событиями. Термин работа может иметь различные значения:

• действительная работа, требующая затрат времени и ресурсов;
• ожидание — процесс, не требующий затрат труда, но занимающий время (например, процессы сушки пиломатериалов, твердения бетона и т.д.);
• фиктивная работа — логическая связь между двумя или несколькими работами (событиями), не требующая затрат труда, материальных ресурсов и времени. Она указывает, что возможность начала одной работы непосредственно зависит от результата другой. Продолжительность фиктивной работы равна нулю.

Событие — это момент завершения какого-либо процесса. Событие может являться частным результатом отдельной работы или суммарным результатом нескольких работ. Конечный результат любой работы важен не только как факт окончания данной работы, но и как необходимое условие для начала следующих работ. Событие не имеет продолжительности во времени. Сетевой график ограничен исходным и завершающим событиями. Исходное событие (источник) не имеет предшествующих работ и событий. Завершающее событие (сток) не имеет последующих работ и событий. У всех событий сети, кроме исходного и завершающего имеются, по крайней мере, по одной непосредственно предшествующей и по одной непосредственно за ним следующей работе. Событие, непосредственно предшествующее работе, по отношению к ней называется начальным, а событие, непосредственно следующее за ней, — конечным. Исходная информация о работах, которые требуется выполнить, должна содержать перечень всех работ, последовательность их выполнения и оценку каждой работы (продолжительность, стоимость и т.п.). Так, например, информация о некотором проекте может быть задана в виде структурной таблицы комплекса работ (табл. 4.1). Т а б л и ц а 4.1

Работа	Опирается на работы	Продолжительность работы
…	…	…

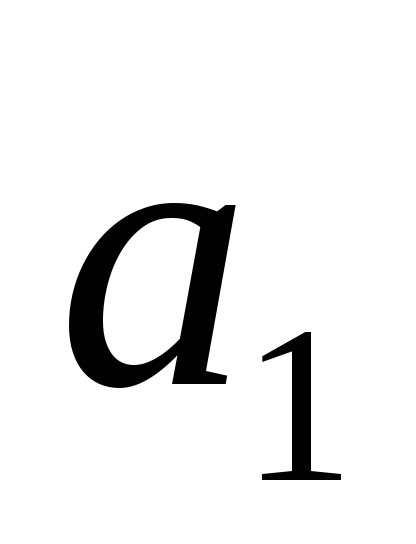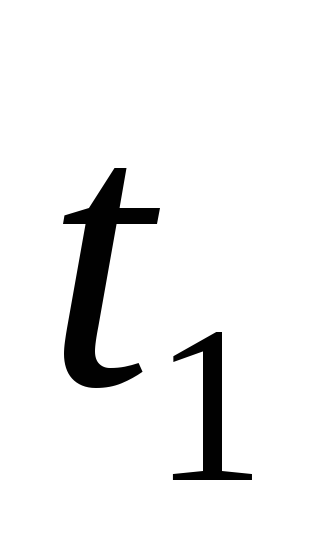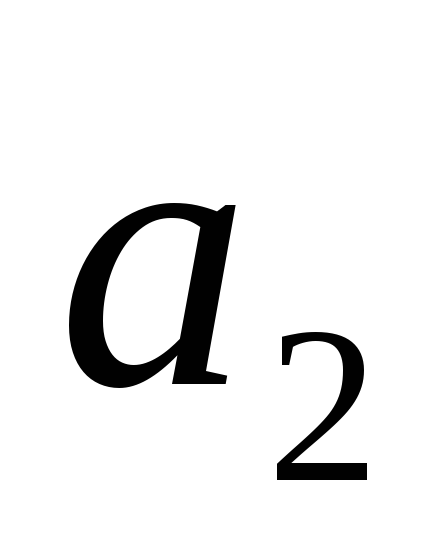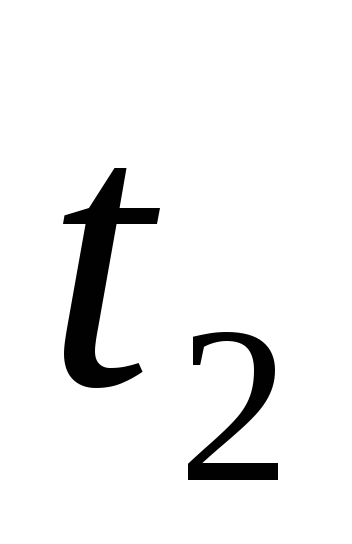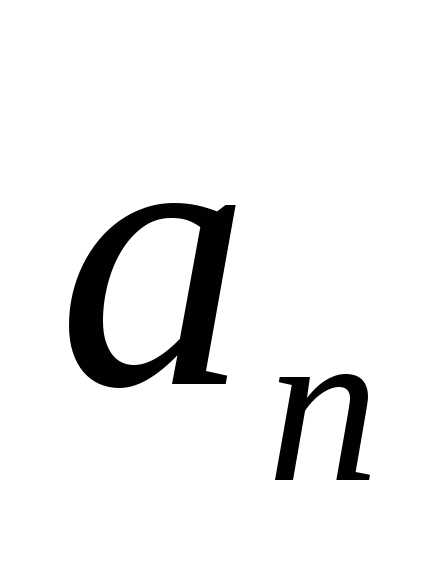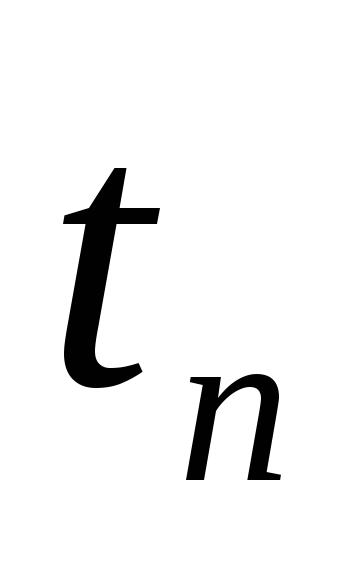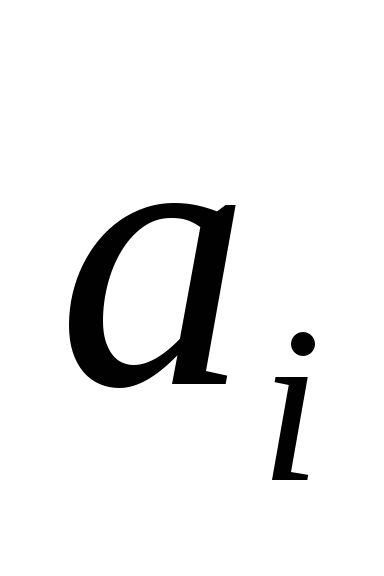
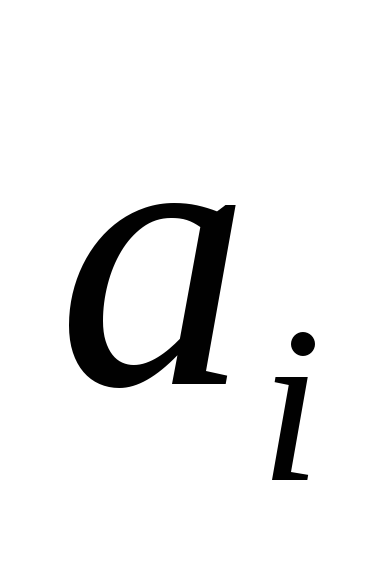
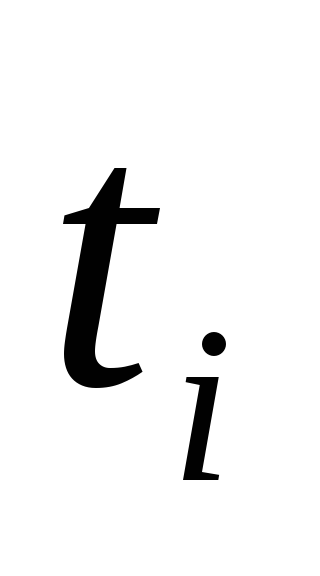
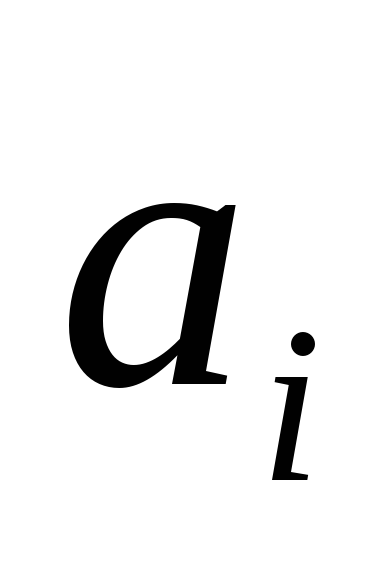
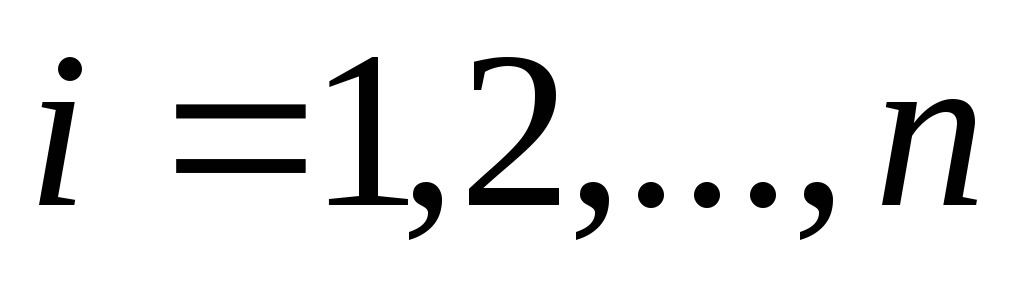
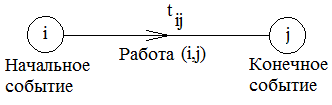
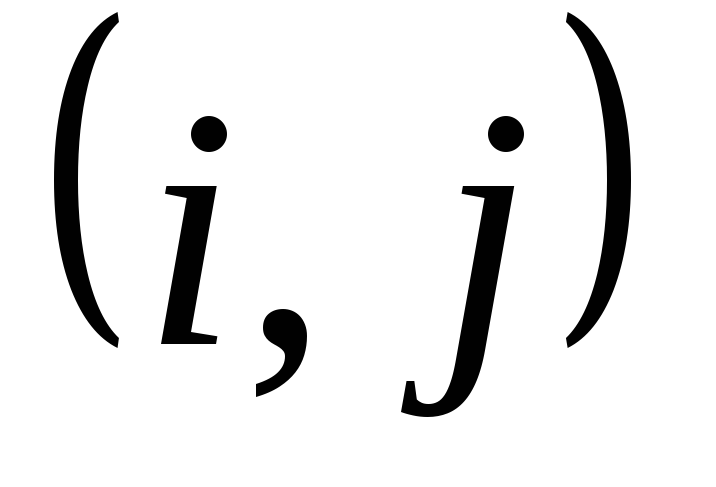
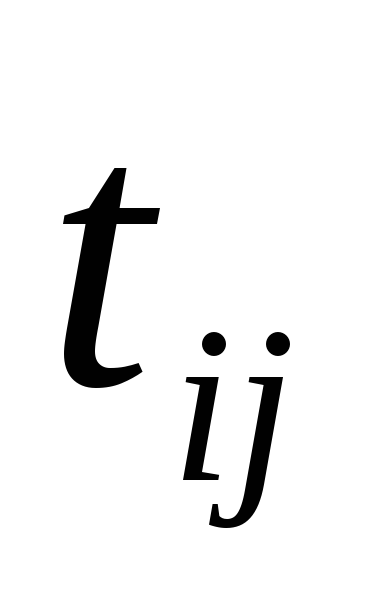
В графе «Работа» перечислены все работы проекта. Напротив работы , в графе «Опирается на работы» указываются все работы, сразу после окончания которых начинается выполнение работы . В графе «Продолжительность работы» указывается время выполнения работы , . Сетевой график строится следующим образом: кружками обозначаются события; стрелками, соединяющими события, обозначаются работы. Сплошными стрелками изображаются действительные работы, пунктирными — ожидания и фиктивные работы. Сетевой график выражает логическую связь в последовательности событий и работ. Для удобства работы с сетью по определению временных параметров необходимо произвести упорядоченную нумерацию событий. События являются упорядоченными, если для каждой работы номер ее начального события меньше номера ее конечного события. Работу в сетевых графиках принято кодировать парой , где– номер начального, а – номер конечного события (рис. 4.1). Рис. 4.1.Связь работы и событий В пронумерованной сети для каждой работы всегда. Продолжительность работыпринять проставлять в сетевом графике над соответствующей стрелкой.

Источник

Анализ сетевого графика

Созданный сетевой график можно сохранить в форматах docx и png (меню Действия ). Далее можно найти параметры сетевой модели (критический путь, резервы времени, построить диаграмму Ганта и многое другое).

Инструкция к сервису

Для добавления вершины на графическое полотно необходимо использовать соответствующую фигуре кнопку Добавить . Новый объект также можно вставить, предварительно выделив его левой кнопкой мыши, а затем щелкнуть мышкой на рабочем поле. Нумерация вершин может начинаться с 0 , для этого нужно снять отметку с пункта Нумерация вершин с №1 .

Чтобы соединить вершины, их необходимо предварительно выбрать (один клик мыши по объекту), а затем нажать на кнопку Соединить .
Сетевая модель может быть представлена в табличной форме и в виде матрицы весов (матрицы расстояний). Чтобы использовать данные представления, выберите меню Операции .

Построенный граф можно сохранить в формате docx или png .
Если в качестве формы вершин используется прямоугольник, то при построении секторальной диаграммы применяется методология Microsoft Visio с отображением параметров duration, ES, EF, LS, LF, and slack.

Основные определения

• «действительная работа» – процесс, требующий затрат времени и ресурсов;
• «фиктивная работа» – логическая связь между двумя или несколькими работами, указывающая на то, что начало одной работы зависит от результатов другой. Фиктивная работа не требует затрат времени и ресурсов, продолжительность ее равна нулю.

Правила построения сетевой модели

• в сети не должно быть «тупиков», т.е., событий, от которых не начинается ни одна работа, исключая завершающее событие графика;
• В сетевом графике не должно быть «хвостовых» событий, то есть событий, которым не предшествует хотя бы одна работа, за исключением исходного.
• в сети не должно быть замкнутых контуров (рис.1);
• Любые два события должны быть непосредственно связаны не более чем одной работой.
• В сети рекомендуется иметь одно исходное и одно завершающее событие.
• Сетевой график должен быть упорядочен. То есть события и работы должны располагаться так, чтобы для любой работы предшествующее ей событие было расположено левее и имело меньший номер по сравнению с завершающим эту работу событием.

Методы оптимизации сетевого графика

Логико-математическое описание, формирование планов и управляющих воздействий осуществляется на базе использования особого класса моделей, называемых сетевыми моделями.
После построения и расчета сетевого графика (определения его параметров), выполнения анализа графика, заключающегося в оценке его целесообразности и структуры, оценке загрузки исполнителей, оценке вероятности наступления завершающего события в заданный срок, следует приступать к оптимизации сетевого графика. Процедура оптимизации заключается в приведение графика в соответствие с заданными сроками выполнения работ, возможностями подрядных организаций и т.д. В общем случае под оптимизацией следует понимать процесс улучшения организации выполнения работ.

• Оптимизация сетевой модели по критерию «число исполнителей». Заполняется столбец Количество исполнителей Ч ►
• Оптимизация сетевой модели по критерию «время – стоимость» ( время — затраты ). В случае известных коэффициентов затрат на ускорение работ заполняется только этот столбец h(i,j) . Иначе, заполняются столбцы t_опт (Нормальный режим), Минимальное время работ, t_min (Ускоренный режим), Нормальная стоимость, Cн и Срочная стоимость, Cc .

Источник

1. Элементы построения сетевых моделей

В основе метода сетевого планирования и управления (СПУ) лежит построение графика, по своему виду напоминающего сеть (переплетение нитей и узелков), поэтому график и получил название сетевого.

Сетевой моделью называется отображение процессов, выполнение которых подчинено достижению одной или нескольких целей, с указанием взаимосвязей между этими процессами.

Сетевым графиком называется график производства работ с установленными расчётом сроками их выполнения. Сетевой график представляет собой графическое изображение сетевой модели с рассчитанными параметрами.

Элементами сетевой модели являются работа, событие и путь:

а) работа – это трудовой процесс, требующий затрат времени и ресурсов.

Название работы является минимальной информацией о работе, содержащейся в сетевой модели (например, отрывка котлована, возведение каркаса, устройство кровли, поставка оборудования и т.д.).

Работа на графике изображается сплошной стрелкой, направленной слева направо с указанием над стрелкой продолжительности работы.

Работа, которая требует лишь затрат времени, называется работа – ожидание. Ожидание на графике изображается пунктирной стрелкой с указанием над стрелкой её продолжительности (например, процесс твердения бетона или ожидание поставки материалов). Эти работы требуют только затрат времени.

Для отображения правильной технологической последовательности между работами применяется зависимость. Ни времени, ни ресурсов «зависимость» не требует. На графике зависимость изображают пунктирной стрелкой, продолжительность которой равна нулю. В литературных источниках зависимость называют фиктивной работой.

Итак, понятие «работа» может иметь три значения:

работа

работа – ожидание

зависимость

б) событие – это итог какой-нибудь деятельности (работы), происходящей мгновенно. Любая работа начинается и заканчивается событием.

Событие не потребляет ни времени, ни трудовых ресурсов, оно обозначает только факт начала и окончания одной или нескольких работ. Событие графически обозначается кружком, внутри которого ставится его номер, или может обозначаться буквами.

Событие, не имеющее непосредственно предшествующих работ, называется исходным, не имеющее непосредственно следующих работ – завершающим. Событие, не являющееся ни исходным, ни завершающим, называется промежуточным.

На рис. 1 событие 1 – исходное, событие 6 – завершающее, события 2, 3, 4, 5 – промежуточные.

Все работы комплекса по отношению друг к другу подразделяются на данную, предшест-вующую и последующую работы. Обозначение работ см. на рис. 2.

в) путь – это непрерывная технологическая последовательность работ от исходного события к завершающему.

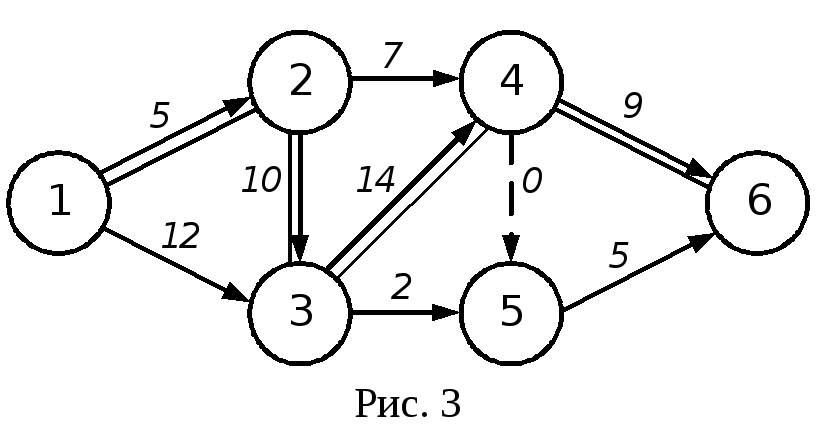
На рис. 3 дан сетевой график из восьми работ, одной зависимости и шести событий. На графике можно выделить 7 путей:

1-й путь проходит по событиям 1, 2, 3, 4, 6;

2-й путь проходит по событиям 1, 3, 5, 6;

3-й путь проходит по событиям 1, 2, 4, 6;

4-й путь проходит по событиям 1, 2, 3, 5, 6;

5-й путь проходит по событиям 1, 2, 3, 4, 5, 6;

6-й путь проходит по событиям 1, 2, 4, 5, 6;

7-й путь проходит по событиям 1, 3, 4, 5, 6.

Зная продолжительность каждой работы t_ij , можно определить продолжительность любого пути сетевого графика.

Продолжительность пути определяется как сумма продолжительностей работ, составляющих этот путь:

Критический путь – это путь, имеющий максимальную продолжительность. Он определяет конечный срок строительства, это самый трудоемкий и неблагоприятный путь.

Подкритический путь – это путь, продолжительность которого близка к продолжительности критического пути.

На рис. 3 длина различных путей от исходного события до завершающего равна:

1-й путь Т₁ = 5 + 10 + 14 + 9 = 38;

4-й путь Т₄ = 5 + 10 + 2 + 3 = 20;

5-й путь Т₅ = 5 + 10 + 0 + 3 = 32;

6-й путь Т₆ = 5 + 7 + 0 + 3 = 15;

7-й путь Т₇ = 12 + 14 + 0 + 3 = 29.

Первый путь имеет наибольшую продолжительность из всех путей, значит, он является критическим.

Критическим путь назван потому, что, во-первых, из всех путей сетевого графика только он определяет общую продолжительность строительства; во-вторых, он указывает на работы, которые являются ведущими для выполнения заданного комплекса работ. Работы, лежащие на критическом пути, называются критическими.

На рис. 3 критическими работами являются 1-2; 2-3; 3-4; 4-6.

На сетевом графике критический путь выделяют красной двойной или жирной линией.

В сетевом графике может быть несколько критических путей одинаковой продолжительности. Определение продолжительности (длины) критического пути и критических работ – одна из основных задач, решаемых в методе сетевого планирования и управления (СПУ).

Источник