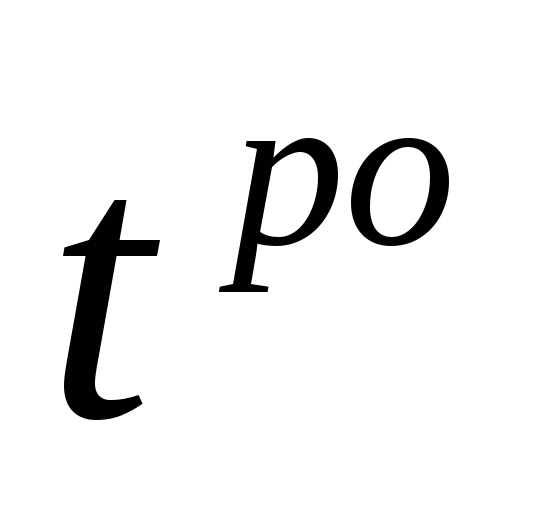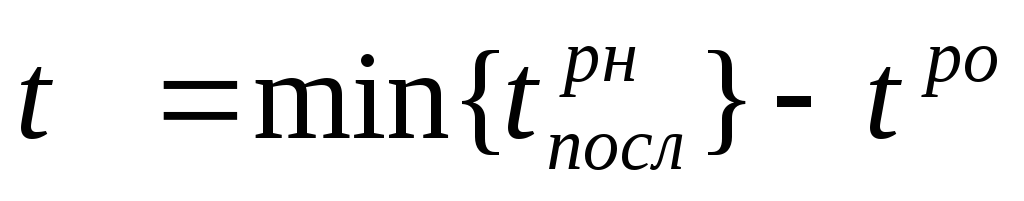3. Сетевое планирование и управление: особенности, правила построения, параметры, методы расчета сетевых графиков, управление с их помощью.
Основным методом решения плановых и управленческих задач в строительстве является метод сетевого планирования и управления (СПУ). Метод СПУ включает: построение, расчет, анализ и оптимизацию сетевых моделей и применяется для решения задач, связанных с планированием и управлением строительства.
Метод СПУ объединяет автоматизированный учет и контроль, выбор и принятие управленческих решений. Результаты расчета сетевой модели содержат оценку выполнения исполнителями работ для достижения поставленной цели. Это позволяет руководителям концентрировать внимание на вопросах, от которых в данный момент времени зависит срок достижения цели. На основе информации о временных, объемных и ресурсных параметрах моделируются варианты регулирующих воздействии, наиболее рациональный из которых применяется. В качестве модели процесса производства используется сетевая модель.
Сетевые модели позволяют лучше всего отобразить порядок возведения сложного объекта, осуществлять научно-обоснованные методы строительства определять и разрешать многие проблемные ситуации в процессе производства строительных работ.
Сетевой график является документом, позволяющим оперативно руководить строительством и перераспределять ресурсы в зависимости от фактического состояния строительства.
Сетевые графики наиболее целесообразны для сооружения сложных промышленных и других комплексов, где участвуют многие организации причем сетевые графики учитывают все работы, от которых зависит успешный ход строительства, в т.ч. проектирование, внешние поставки материалов, технологического оборудования и др.
Сетевые модели используются в строительстве для решения задач перспективного планирования, определения продолжительности и сроков выполнения основных этапов создания объектов (проектирования, строительно-монтажных работ поставки технологического оборудования, освоения производственной мощности), а также планирование капитальных вложений по периодам строительства объекта.
Сетевые модели используются также для решения задач оперативного планирования строительным производством по отдельному объекту, зданий, сооружений.
Сетевые модели бывают разные в зависимости от характера объекта строительства, целей и ряда других показателей.
Классифицируются сетевые модели по следующим основным признакам:
1. по виду целей — одноцелевые модели и многоцелевые (например, при строительстве разных объектов, возводимых одной строительной организацией);
2. по числу охвата объектов — частная модель и комплексная (например, на один объект и на весь промышленный комплекс завода);
3. по характеру оценок параметров модели: детерминированные (с заранее и полностью обусловленными данными) и вероятностные (учитывающие влияние случайных факторов);
4. модели с учетом целевой направленности — временные, ресурсные, стоимостные.
Сетевая модель с требуемой степенью детализации отображает взаимосвязь отдельных работ по возведению объекта (комплекса) и дает возможность осуществить математический анализ календарного плана, прогнозировать его будущее состояние, а также оценивать эффективность принимаемых решений.
Сетевой моделью называется ориентированный граф, отражающий последовательность и организационно-технологические взаимосвязи между работами, выполнение которых необходимо для достижения поставленной цели.
Сетевая модель, представленная графически на плоскости с рассчитанными временными и ресурсными параметрами, называется сетевым графиком. Сетевые графики используются для расчета временных параметров и оптимизации календарных планов.
Правила построения сетевых графиков
Для построения сетевого графика необходимо выявить последовательность и взаимосвязь работ: какие работы необходимо выполнить, и какие условия обеспечить, чтобы можно было начать данную работу, какие работы можно и целесообразно выполнять параллельно с данной работой, какие работы можно начать после окончания данной работы. Эти вопросы позволяют выявить технологическую взаимосвязь между отдельными работами, обеспечивают логическое построение сетевого графика и его соответствие моделируемому комплексу работ.
Уровень детализации сетевого графика зависит от сложности строящегося объекта, количества используемых ресурсов, объемов работ и продолжительности строительства.
Имеется два типа сетевых графиков:
Сетевые графики типа «вершины — работы».
Элементами такого графика являются работы и зависимости. Работа представляет собой определенный производственный процесс, требующий затрат времени и ресурсов для его выполнения, и изображается прямоугольником. Зависимость (фиктивная работа) показывает организационно-технологическую связь между работами, не требующую затрат времени и ресурсов, изображается стрелкой. Если между работами имеется организационный или технологический перерыв, то на зависимости указывается длительность этого перерыва.
Если работа сетевого графика «вершины — работы» не Имеет предшествующих работ, то она является исходной работой этого графика. Если работа не имеет последующих работ, То она является завершающей работой сетевого графика. В сетевом графике «вершины — работы» не должно быть замкнутых контуров (циклов), т.е. зависимости не должны возвращаться в ту работу, из которой они вышли.
Сетевые графики типа «вершины — события».
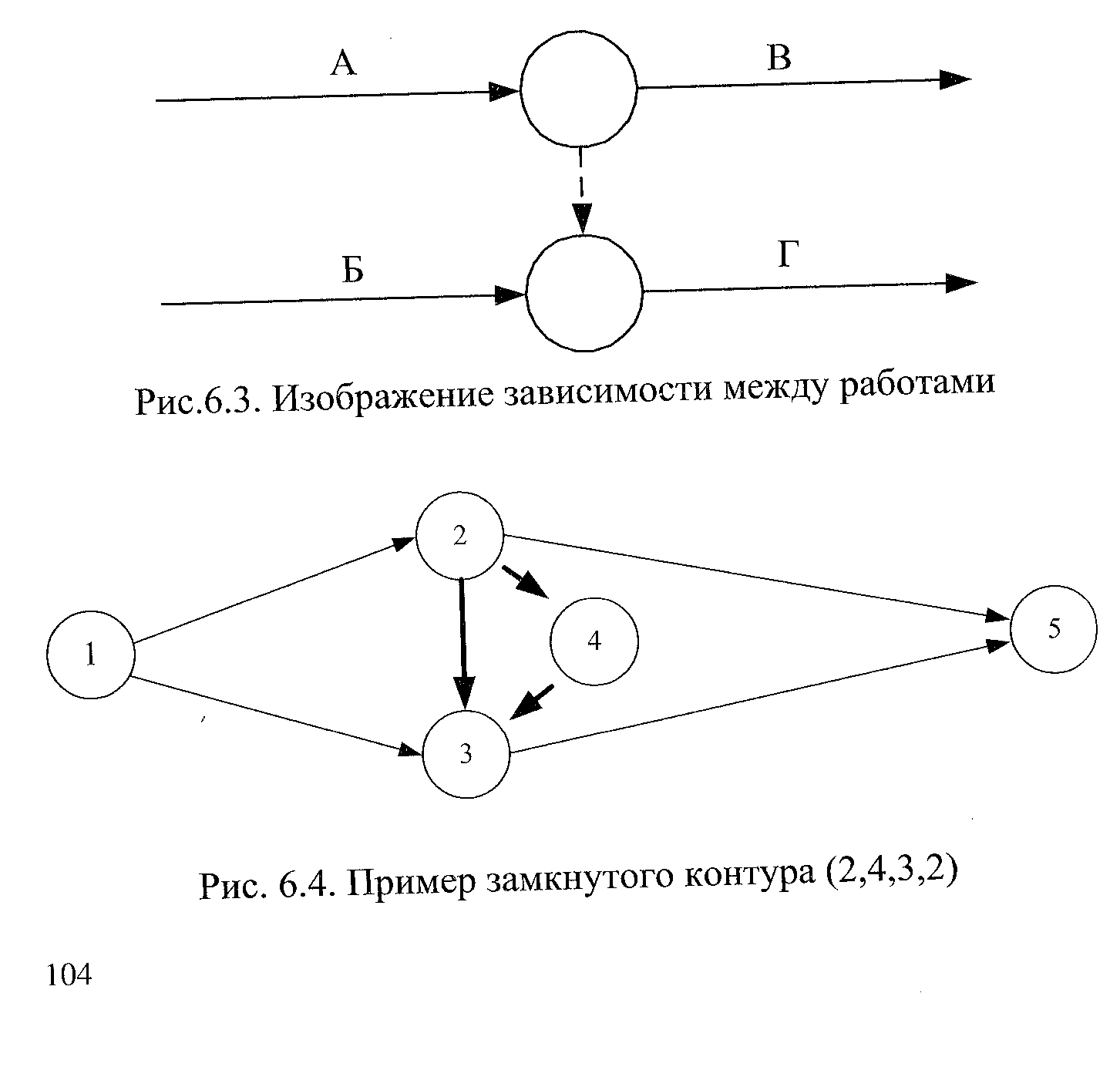
Элементами такого типа графиков являются работы, зависимости и события. Работа изображается сплошной стрелкой, зависимость — пунктирной. Событие представляет собой результат одной или нескольких работ, необходимый и достаточный для начала одной или нескольких последующих работ, и изображается кружком.
В сетевых графиках этого типа каждая работа находится между двумя событиями: начальным, из которого она выходит, и конечным, в которое она входит. События сетевого графика нумеруются, поэтому каждая работа имеет код, состоящий из номеров ее начального и конечного события.
Например на рис. 6.2 работы закодированы как (1,2); (2,3); (2,4); (4,5)
Если событие сетевого графика «вершины — события» не имеет предшествующих работ, то оно является исходным событием этого графика. Следующие непосредственно за ним работы называются исходными. Если событие не имеет последующих работ, то оно является завершающим событием. Входящие в него работы называются завершающими.
для правильного отображения взаимосвязей между работами необходимо соблюдать следующие основные правила построения сетевого графика «Вершины — события»:
1. При изображении одновременно или параллельно выполняемых работ (например, работ «Б» и «В» на рис.6.2) вводятся зависимость (3,4) и дополнительное событие (3).
2. Если для начала работы «Г» необходимо выполнить работы «А» и «Б», а для начала работы
З. В сетевом графике не должно быть замкнутых контуров (циклов), т.е. цепочки работ, возвращающейся к тому событию, из которого они вышли
4. В сетевом графике при поточной организации строительства вводятся дополнительные события и зависимости (рис. 6.5.).
Для определения продолжительности критического пути и сроков выполнения каждой работы определяют следующие временные параметры:
• раннее начало работы —
• раннее окончание работы — ;
• позднее начало работы — ;
• позднее окончание работы —
• свободный резерв времени — г.
Раннее начало работы — самый ранний момент начала работы. Раннее начало исходных работ сетевого графика равно нулю. Раннее начало любой работы равно максимальному раннему окончанию предшествующих работ:
Раннее окончание работы — самый ранний момент окончания данной работы. Он равен сумме раннего начала и продолжительности работы.
Позднее окончание работы — самый поздний момент окончания работы, при котором продолжительность критического пути не изменится. Позднее окончание завершающих работ равно продолжительности критического пути. Позднее окончание любой работы равно минимальному позднему на чалу последующих работ.
Позднее начало работы — самый поздний момент начала работы, при котором продолжительность критического пути не изменится. Он равен разности между поздним окончанием данной работы и ее продолжительностью.
У работ критического пути ранние и поздние сроки начала и окончания равны между собой, поэтому они не имеют резервов времени. Работы, не лежащие на критическом пути, имеют резервы времени.
Полный резерв времени — максимальное время, на которое можно увеличить продолжительность работы или пере нести ее начало без увеличения продолжительности критического пути. Он равен разности между поздним и ранним сроком начала или окончания работы.
Свободный резерв времени — время, на которое можно увеличить продолжительность работы или перенести ее начало, не изменив при этом раннего начала последующих работ. Он равен разности между ранним началом последующей работы и ранним окончанием данной работы.
Расчет сетевого графика «вершины — работы»
Для расчета сетевого графика «вершины — работы» прямоугольник, изображающий работу, делят на 7 частей (рис.6.6).
В верхних трех частях прямоугольника записываются раннее начало, продолжительность и раннее окончание работы, в трех нижних позднее начало, резервы времени и позднее окончание. Центральная часть содержит код (номер) и наименование работы.
Расчет сетевого графика начинается с определения ранних сроков. Ранние начала и окончания вычисляются последовательно от исходной до завершающей работы. Раннее начало исходной работы равно О, раннее окончание — сумме раннего начала и продолжительности работы:
Раннее начало последующей работы равно раннему окончанию предыдущей работы. Если данной работе непосредственно предшествуют несколько работ, то ее раннее начало будет равно максимальному из ранних окончаний пред шествующих работ:
Таким образом, определяются ранние сроки всех работ сетевого графика и заносятся в верхние правую и левую части.
Раннее окончание завершающей работы определяет продолжительность критического пути.
Расчет поздних сроков ведется в обратном порядке от завершающей до исходной работы. Позднее окончание завершающей работы равно ее раннему окончанию, т.е. продолжительности критического пути.
Позднее начало определяется как разность позднего окончания и продолжительности:
Позднее начало последующих работ становится поздним окончанием предшествующих работ. Если за данной работой непосредственно следуют несколько работ, то ее позднее окончание будет равно минимальному из поздних начал по следующих работ:
Подобным образом определяются поздние сроки всех работ сетевого графика и записываются в левую и правую нижние части.
Полный резерв времени, равный разности поздних и ран них сроков, заносится в числитель середины нижней части:
Свободный резерв времени, равный разности между минимальным ранним началом последующих работ и ранним окончанием данной работы, записывается в знаменатель сере дины нижней части:
Свободный резерв всегда меньше или равен полному резерву работы.
1.2 Основные понятия сетевого планирования
Следует выделить следующие понятия, необходимые для сетевого планирования.
Работа – производственный процесс, требующий затрат времени и материальных ресурсов и приводящий к достижению определенных результатов.
По своей физической природе работы можно рассматривать как действие (например, заливка фундамента бетоном, составление заявки на материалы, изучение конъюнктуры рынка), процесс (пример — старение отливок, выдерживание вина, травление плат) и ожидание (процесс, требующий только затраты времени и не потребляющий никаких ресурсов; является технологическим (твердение цементной стяжки) или организационным (ожидание сухой погоды) перерывом между работами, непосредственно выполняемым друг за другом.
По количеству затрачиваемого времени работа может быть:
- действительной, то есть протяжённым во времени процессом, требующим затрат ресурсов;
- фиктивной (или зависимостью), не требующей затрат времени и представляющей связь между какими-либо работами: передача измененных чертежей от конструкторов к технологам, сдача отчета о технико-экономических показателях работы цеха вышестоящему подразделению.
1.3 Правила построения сетевых моделей
- какие работы должны быть завершены до начала данной работы;
- какие работы должны быть начаты после завершения данной работы;
- какие работы необходимо выполнять одновременно с выполнением данной работы.