Порядок и правила построения сетевых графиков
Сетевые графики составляются на начальном этапе планирования. Вначале планируемый процесс разбивается на отдельные работы, составляется перечень работ и событий, придумываются их логические связи и последовательность выполнения, работы закрепляются за ответственными исполнителями. С их помощью оценивается длительность каждой работы. Затем составляется (сшивается) сетевой график. После упорядочения сетевого графика рассчитываются параметры событий и работ, определяются резервы времени и критический путь. Проводят анализ и оптимизация сетевого графика, который при необходимости вычерчивается заново с пересчетом параметров событий и работ.
При построении сетевого графика необходимо соблюдать ряд правил:
1) все стрелки сетевого графика имеют общее направление (слева направо);
2) между парой событий может быть изображена только одна работа;
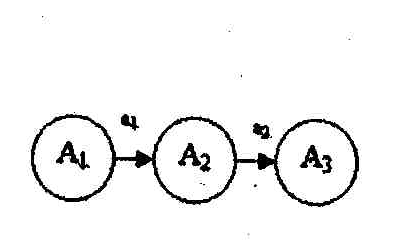
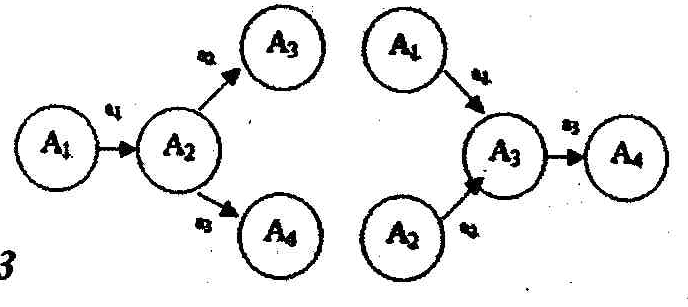
3) используются возможные варианты следования событий и работ (табличная запись и пути перехода приведены на рис. 1);
4) в сетевой модели не должно быть «тупиковых» событий, то есть событий, из которых не выходит ни одна работа, за исключением завершающего события;
5) в сетевом графике не должно быть «хвостовых» событий (кроме исходного), которым не предшествует хотя бы одна работа;
6) все события, кроме исходного и завершающего, должны иметь как входящие, так и выходящие стрелки;
7) если две работы начинаются в одно и то же время, в одном событии и оканчиваются в другом событии, то вводят фиктивное событие и фиктивную работу. При этом одна из параллельных работ замыкается на это фиктивное событие. Фиктивные работы имеют нулевую продолжительность и изображаются на графике пунктирными линиями;
8) в сети не должно быть замкнутых контуров и петель, то есть путей, соединяющих некоторые события с ними же самими.
Упорядочение сетевого графика. Понятие о пути
Предположим, что при составлении некоторого проекта выделено 12 событий – 0,1,2,3,4,5,6,7,8,9,10,11 и 24 связывающие их работы – (0,1), (0,2), (0,3), (1,2), (1,4), (1,5), (2,3), (2,5), (2,7), (3,6), (3,7), (3,10), (4,8), (5,8), (5,7), (6,10), (7,6), (7,8), (7,9), (7,10), (8,9), (9,11), (10,9), (10,11). Необходимо составить и упорядочить сетевой график.
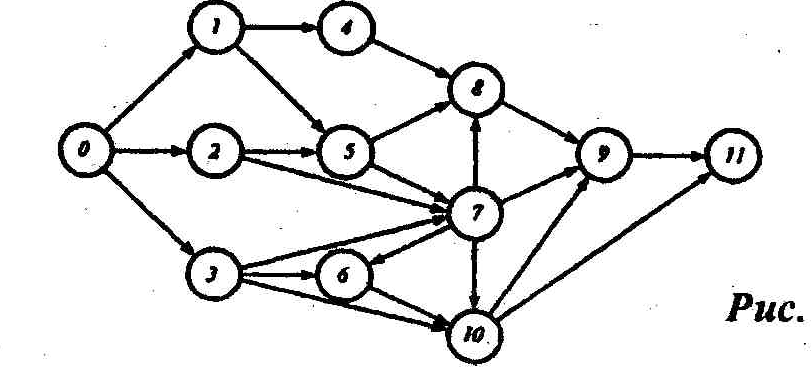
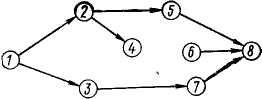
Как следует из перечня работ, исходным событием является событие 0 (ему не предшествуют никакие работы), а завершающим – событие 11 (за ним не следует ни одна работа). Полагая на сетевых графиках изменении времени слева направо, поместим событие 0 в левую часть графика, а событие 11 – в правую часть, разместив между ними промежуточные события в некотором порядке, соответствующем их номерам (рисунок 2). События свяжем работами-стрелками в соответствии с перечнем работ.
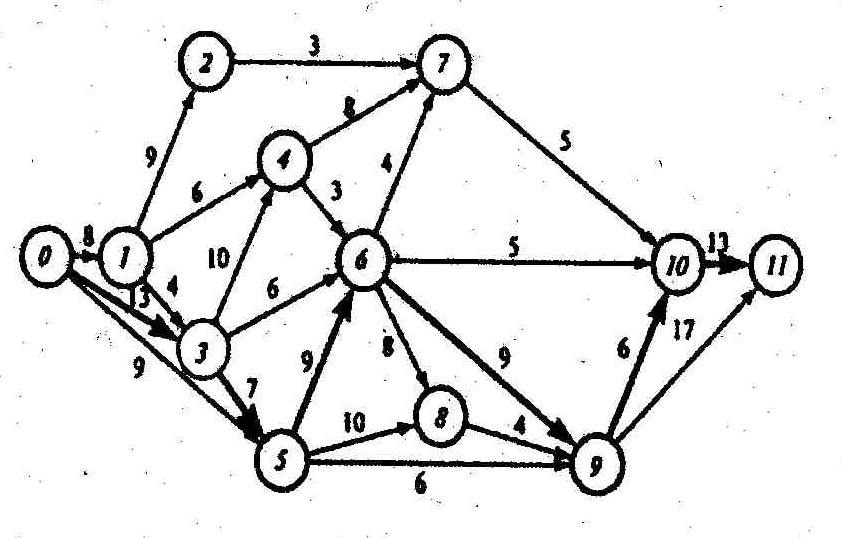
Упорядочение сетевого графика заключается в таком расположении событий и работ, при котором для любой работы предшествующее ей событие расположено левее и имеет меньший номер по сравнению с завершающим эту работу событием. Другими словами, в упорядоченном сетевом графике: от событий с меньшими номерами к событиям с большими номерами (рисунок 3).
Одно из важнейших понятий сетевого графика – понятие пути.
Путь – любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы.
Среди различных путей сетевого графика наибольший интерес представляет полный путь L – любой путь, начало которого совпадает с исходным событием сети, а конец – с завершающим.
Наиболее продолжительный полный путь в сетевом графике называется критическим. Критическими называются также работы и события, расположенные на этом пути.
Например, для рассматриваемого нами сетевого графика (рисунок 3) полными путями будут: путь 0→1→2→7→10→11 продолжительностью 8+9+3+5+13=38 суток, путь 0→1→3→4→6→10→11 продолжительностью 8+4+10+3+5+13=43 суток, путь 0→3→5→6→9→10→11 продолжительностью 13+7+9+13+6+13=61 суток и т.д.
Последний путь имеет наибольшую продолжительность (не только среди приведенных четырех полных путей, но и среди всех полных путей, которых в данном случае насчитывается 64), поэтому он и является критическом. Продолжительность критического пути составляет 61 сутки, то есть для проведения комплекса работ понадобятся 61 сутки. Быстрее комплекс выполнить нельзя, так как для достижения завершающего события критический путь надо пройти обязательно.
Для достижения события 11 надо выполнить работу (10,11), то есть достичь события 10; для достижения события 10 надо провести работу (9,10), то есть достичь события 9; для достижения события 9 надо достичь работу (6,9), то есть достичь события 6, и т.д.
Определив критический путь, установили критические события сети 0,3,5,6,9,10,11 и критические работы (0,3), (3,5), (5,6), (6,9), (9,10), (10,11).
Критический путь имеет особое значение в системе СПУ, так как работы этого пути определяют общий цикл завершения всего комплекса работ, планируемых при помощи сетевого графика. И для сокращения продолжительность проекта необходимо в первую очередь сокращать продолжительность работ, лежащих на критическом пути.
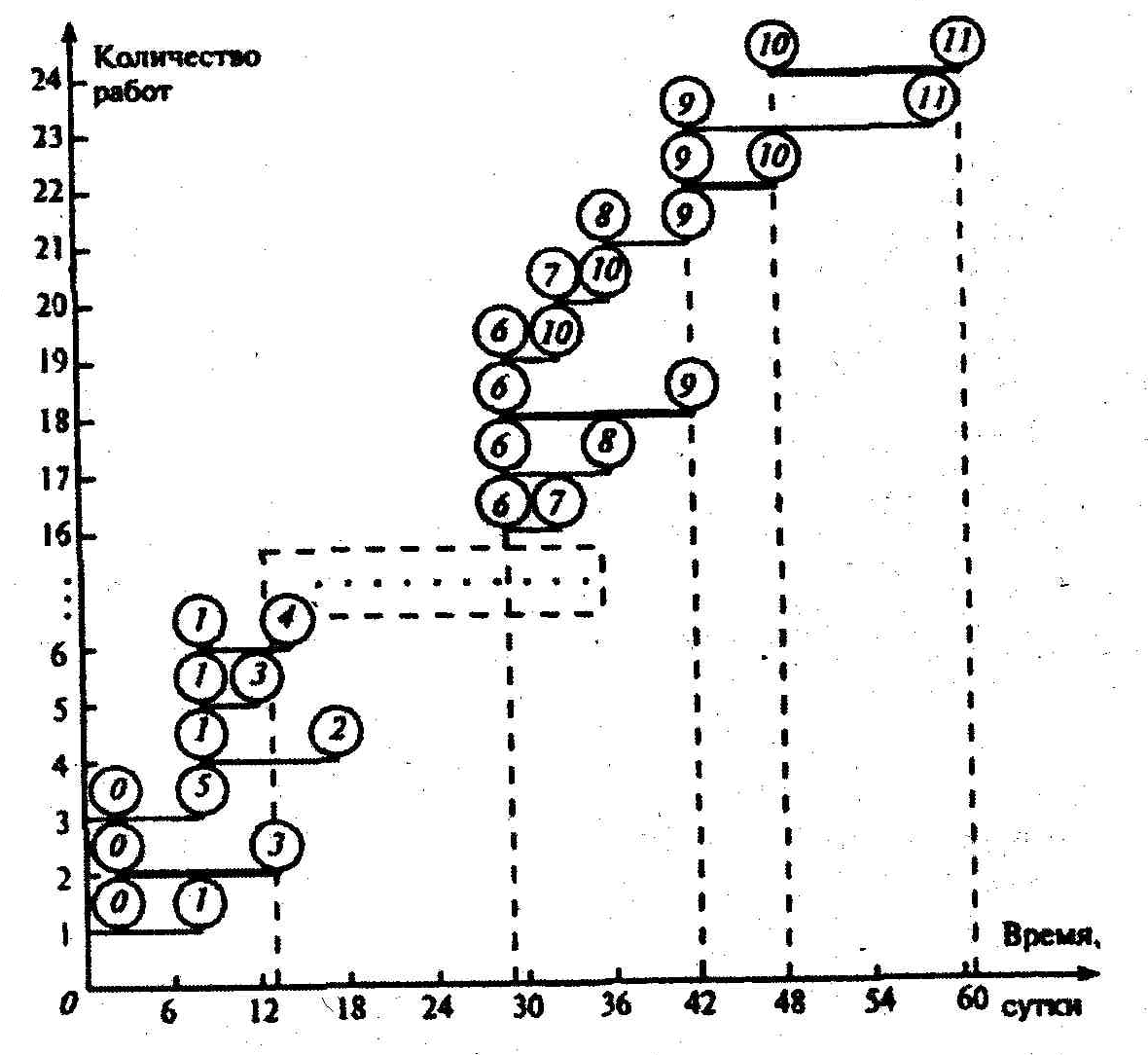
Классический вид сетевого графика – сеть, вычерченная без масштаба времени. Поэтому сетевой график, хотя дает четкое представление о порядке следования работ, но недостаточно нагляден для определения тех работ, которые должны выполняться в каждый данный момент времени. В связи с этим небольшой проект после упорядочения сетевого графика рекомендуется дополнить линейной диаграммой проекта. Такая линейная диаграмма для рассматриваемой сети показана на рисунке 4.
При построении линейной диаграммы каждая работа изображается параллельным оси времени отрезком, длина которого равна продолжительности этой работы. При наличии фиктивной работы нулевой продолжительности (в рассматриваемой сети ее нет) она изображается точкой. События i и j , начало и конец работы (i, j) помещают соответственно в начале и конце отрезка. Отрезки располагают один над другим, снизу вверх в порядке возрастания индекса i , а при одном и том же i – в порядке возрастания индекса j (на рисунке 4 вследствие ограниченности места не показаны работы-отрезки, выходящие из 2-, 3-, 4- и 5-го событий).
По линейной диаграмме проекта можно определить коритическое время, критический путь, а также резервы времени всех работ.
Критическое время комплекса работ равно координате на оси времени самого правого конца всех отрезков диаграммы:
ТКР=t(11) =61 суток
Для определения критического пути рассматриваются работы-отрезки, конечные события которых совпадают с завершающим событием сети (в примере (9,11) и (10,11). Затем находят отрезок (9,10), правый конец которого лежит на одной вертикали (10) с левым концом одного из рассматриваемых ранее отрезков (10,11). Аналогично определяют и другие работы-отрезки критического пути: (6,9),….(0,3) (на рис. 4 они все выделены жирным шрифтом).
3 Правила построения сетевых графиков
Любая работа сетевой модели соединяет два события: начальное событие работы и конечное событие работы. Для однозначного обозначения работ используют идентификаторы (i, j), где i — номер начального события работы, j — номер конечного события работы. Обычно на сетевых графиках события упорядочены, то есть i j.
Каждая работа должна иметь определение, означающее ее содержание (например, составление сметы, подбор кадров, монтаж оборудования, выкладка товаров и т. д.). Наименование (содержание) работы указывают под стрелкой, а продолжительность — над стрелкой. Всем стрелкам сетевого графика задают общее направление слева направо. События нумеруют последовательно слева направо и сверху вниз.
При построении сетевых графиков соблюдают следующие правила:
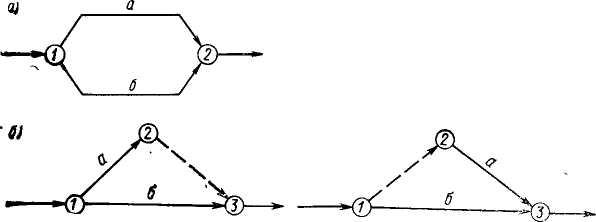
1) между каждыми двумя событиями может быть изображена только одна работа. Параллельно выполняемые работы нельзя изображать через их общее начальное и конечное событие. Для их правильного изображения вводят дополнительные события и зависимости (рисунок 6.3);
Рисунок 6.3 — Построение параллельно выполняемых работ:
а — неправильно; б — правильно
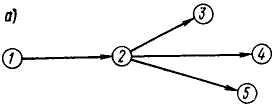
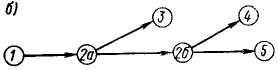
2) если какие-либо работы в сети, например, работы (2,3) и (2,4) (рисунок 6.4), могут быть начаты до полного окончания непосредственно предшествующей им работы (1,2), то последняя (работа (1,2)) может быть выражена как сумма отдельных ее частей (1,2а) и (2а, 2б), выполнение которых необходимо и достаточно для начала следующих за ними работ. После выполнения работы (1,2а) можно начать работу (2а, 3), после (2а, 2б) – работу (2б, 4) и т.д.;
Рисунок 6.4 — Разделение работы (1,2) на части, необходимые и достаточные для начала работ (2а, 3); (2б, 4); (2б, 5):
а — работы (2,3), (2,4), (2,5) ждут полного окончания работы (1,2);
б — работы (2,3), (2,4) могут быть начаты, не ожидая окончания всей работы (1,2)
3) в сетевом графике для отражения взаимосвязей между работами применяют зависимости (фиктивные работы). Так, например, фиктивная работа (6,7) (см рисунок 6.1) означает, что возможность начала работ (7,8) зависит не только от выполнения работы (6,7), но и от работы (5,6);
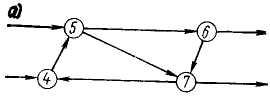
4) в сетевом графике нельзя допускать «замкнутых контуров» (циклов), т. е. путей, состоящих из работ, направление стрелок которых создает замкнутую цепь, как это показано на рисунке 6.5. Наличие замкнутых контуров свидетельствует об ошибках или при построении сетевого графика, или при составлении исходных данных и исключает возможность правильно выполнять расчет параметров сетевого графика;
Рисунок 6.5 — Примеры недопустимых замкнутых контуров:
а — замкнутые контуры 4-5-6-7-4; 4-5-7-4;
б — замкнутый контур 5-6-7-5.
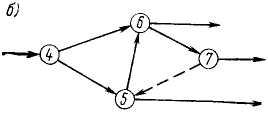
5) в сетевом графике нельзя допускать «тупиков» т. е. событий, кроме завершающего, из которых не выходит ни одной работы, например событие 4 (рисунок 6.6). Наличие «тупиков» показывает, что не выявлены полностью взаимосвязи или в графике показаны излишние работы, которые фактически не влияют на достижение конечной цели;
Рисунок 6.6 — Пример неправильного построения участка сети
с недопустимыми тупиками (событие 4) и хвостами (событие 6)
6) в сети не должно быть событий, за исключением исходного, в которые не входит ни одна работа, например событие 6 (рисунок 6.6).
Разработка сети всегда проводится без учета масштаба времени составляющих его работ. Поэтому длина стрелки-работы в каждом отдельном случае зависит только от необходимости обеспечить простую и четкую структуру сетевого графика и разместить соответствующие показатели на каждой работе. Как правило, за основу построения сети берут технологическую взаимосвязь и последовательность составляющих ее работ. Ресурсные ограничения на этой стадии разработки в основном не учитывают.
После того как построен первый вариант сети, проверяют правильность и точность ее построения. Для этого всю сеть просматривают от исходного события к завершающему и обратно. У каждого события проверяют, все ли предшествующие работы необходимы для того, чтобы начать следующие за ними работы. Детально проверяют все сложные события.
Если в процессе проверки выявляют те или иные неточности в топологии сети, то ошибки направляют включением дополнительных событий и зависимостей, с помощью которых устраняют неверные связи и зависимости и восстанавливают логику сетевого графика.
Первоначальный вариант сети в большинстве случаев необходимо графически упорядочить. График перестраивают таким образом, чтобы уменьшить количество взаимно пересекающихся работ и зависимостей и расположить работы и события соответственно последовательности протекаемого процесса.