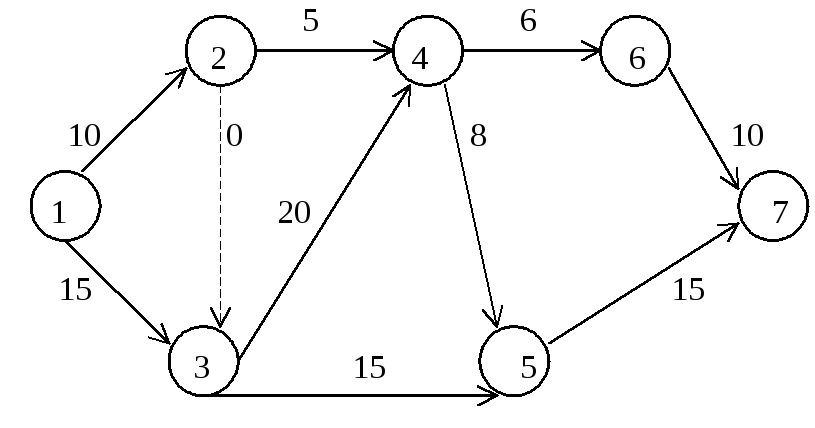
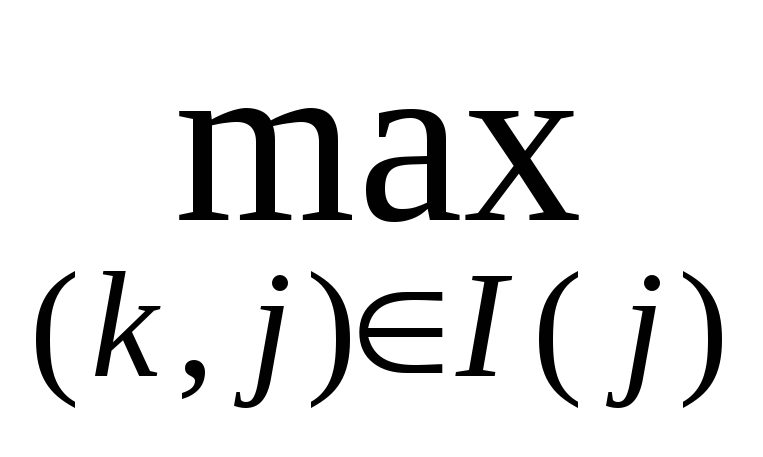Анализ сетевого графика
Созданный сетевой график можно сохранить в форматах docx и png (меню Действия ). Далее можно найти параметры сетевой модели (критический путь, резервы времени, построить диаграмму Ганта и многое другое).
Инструкция к сервису
Для добавления вершины на графическое полотно необходимо использовать соответствующую фигуре кнопку Добавить . Новый объект также можно вставить, предварительно выделив его левой кнопкой мыши, а затем щелкнуть мышкой на рабочем поле. Нумерация вершин может начинаться с 0 , для этого нужно снять отметку с пункта Нумерация вершин с №1 .
Чтобы соединить вершины, их необходимо предварительно выбрать (один клик мыши по объекту), а затем нажать на кнопку Соединить .
Сетевая модель может быть представлена в табличной форме и в виде матрицы весов (матрицы расстояний). Чтобы использовать данные представления, выберите меню Операции .
Построенный граф можно сохранить в формате docx или png .
Если в качестве формы вершин используется прямоугольник, то при построении секторальной диаграммы применяется методология Microsoft Visio с отображением параметров duration, ES, EF, LS, LF, and slack.
Основные определения
- «действительная работа» – процесс, требующий затрат времени и ресурсов;
- «фиктивная работа» – логическая связь между двумя или несколькими работами, указывающая на то, что начало одной работы зависит от результатов другой. Фиктивная работа не требует затрат времени и ресурсов, продолжительность ее равна нулю.
Правила построения сетевой модели
- в сети не должно быть «тупиков», т.е., событий, от которых не начинается ни одна работа, исключая завершающее событие графика;
- В сетевом графике не должно быть «хвостовых» событий, то есть событий, которым не предшествует хотя бы одна работа, за исключением исходного.
- в сети не должно быть замкнутых контуров (рис.1);
- Любые два события должны быть непосредственно связаны не более чем одной работой.
- В сети рекомендуется иметь одно исходное и одно завершающее событие.
- Сетевой график должен быть упорядочен. То есть события и работы должны располагаться так, чтобы для любой работы предшествующее ей событие было расположено левее и имело меньший номер по сравнению с завершающим эту работу событием.
Методы оптимизации сетевого графика
Логико-математическое описание, формирование планов и управляющих воздействий осуществляется на базе использования особого класса моделей, называемых сетевыми моделями.
После построения и расчета сетевого графика (определения его параметров), выполнения анализа графика, заключающегося в оценке его целесообразности и структуры, оценке загрузки исполнителей, оценке вероятности наступления завершающего события в заданный срок, следует приступать к оптимизации сетевого графика. Процедура оптимизации заключается в приведение графика в соответствие с заданными сроками выполнения работ, возможностями подрядных организаций и т.д. В общем случае под оптимизацией следует понимать процесс улучшения организации выполнения работ.
- Оптимизация сетевой модели по критерию «число исполнителей». Заполняется столбец Количество исполнителей Ч ►
- Оптимизация сетевой модели по критерию «время – стоимость» ( время — затраты ). В случае известных коэффициентов затрат на ускорение работ заполняется только этот столбец h(i,j) . Иначе, заполняются столбцы tопт (Нормальный режим), Минимальное время работ, tmin (Ускоренный режим), Нормальная стоимость, Cн и Срочная стоимость, Cc .
Лекция 8. Сетевые модели процессов и событий
1. Исходное понятие: граф, сетевая модель, сетевой график и др.
3. Правильная нумерация вершин сетевого графика.
4. Общая формальность правил построения сетевого графика.
5. Преобразование сетевого графика в сетевой график процессов и событий.
6. Рекомендуемый график построения СМ комплекса процессов и событий.
Комплекс процессов и событий – совокупность взаимосвязанных процессов и событий, составляющих проект.
Процесс – деятельность того или иного вида, направленная на достижение результата поставленной цели.
Целереализующая система – совокупность взаимосвязанных субъектов, а также предметов и средств деятельности, выполняющих инновационный проект.
Событие – это определенное состояние в процессе выполнения проекта.
Граф – это абстрактное представление, множество элементов, с заданными на нем множеством отношений. Например, Г=.
В сетевом моделировании в графе есть вершины и дуги.
Ориентированная дуга – направленная.
Неориентированная – ребро графа.
Не имеющая входящих/выходящих дуг вершина – изолированная вершина.
Сетевая модель процесса и/или событий – ориентированный граф.
Сетевой график – графическая форма представления сетевой модели.
Любая конкретная сетевая модель имеет содержание и форму.
Содержание сетевой модели определяется содержательным смыслом вершин и дуг.
Основными формами являются:
Известны 3 типа сетевых моделей:
1. Вершины обозначают процессы, а дуги – связи между процессами.
2. Вершины обозначают событие, а дуги – процессы (наиболее полная).
3. Вершины обозначают события, а дуги – связи между событиями.
| Форма\Содержание | 1 СМП | 2 СМПС | 3 СМС |
| 1 Графическая (Сетевой график) | 3.1. СГ процессов и связей между ними | 3.2. СГ процессов и событий | 3.3. СГ событий и связей между ними |
| 2 Список | 2.1. Список процессов и связей | 2.2. Список процессов и событий. | 2.3. Список событий проекта |
| 3 Матрица | 3.1. Матрица процессов и связей | 3.2. Матрица процессов и событий | 3.3. Матрица событий и связей |
Для классификации СМ могут использоваться и другие классификационные признаки, например, уровень подробности СМ.
1. СМ используется как удобное средство для описания комплексных процессов и событий.
2. СМ используется для расчета некоторых параметров проекта, например, продолжительность и сроки выполнения всего проекта.
III. Правильная нумерация вершин сетевого графика.
Нумерация вершин является правильной, если для любой дуги (i; j) выполнено условие i < j.
Алгоритм правильной нумерации:
1. Присвоить №1 исходной вершине.
2. Отметить меткой (риской) все дуги, выходящие из исходной вершины (или данной вершины). Риска=метка.
3. Найти такие вершины, для которых все входящие дуги отмечены меткой.
4. Отметить очередной номер той вершины, для которой отмечены все входящие дуги. Если таких вершин несколько, то присвоить им последовательные номера, в любом удобном порядке.
5. Отметить риской все дуги, выходящие из вновь пронумерованных вершин. Если таких дуг нет, то нумерация закончилась. Если такие дуги есть, то шаг №3.
6. Присвоенные номера вершин используются для копирования дуг.
IV. Общие формально-логические правила построения сетевого графика.
При построении СГ должны соблюдаться следующие формально-логические правила:
1. Две смежные вершины связаны только одной дугой.
2. Между любыми двумя вершинами в СГ должен существовать путь, связывающий эти вершины (в СГ не должно быть изолированных вершин).
3. Любая вершина, кроме исходной, должна иметь входящие дуги.
4. Любая вершина СГ, кроме завершающей, должна иметь исходящие дуги.
5. В СГ не должно быть замкнутых контуров (циклов), которые соединяют какую-либо вершину с самой собой.
6. В СГ не должно быть вершин с одинаковым номером, и не должно быть с одинаковым кодом.
7. Если вершины СГ пронумерованы, то для любой дуги (i, j) -> i < j.
V. Преобразование СГ процессов в СГ процессов и событий.
Два СГ называются эквивалентными, если они отражают один и тот же комплеекс процессов и событий.
Преобразование СГП в СГПС выполняется в 2 шага:
1. Формальные преобразования СГП в СГПС путем замены каждой вершины из СГП на дугу с двумя вершинами СГП.
2. Упрощение СГПС. Для этого используются различные приемы.
VI. Рекомендуемый порядок построения СМ комплекса процессов и событий.
Указывается предпочтительный вариант, содержательный тип (СГП, СГС, СГПС).
К постановке задачи указываются требования:
— Формально логическая правильность
— Правильные наименования событий: ПЗ, табл. 1 + СГП, СГПС + табл. 2, отчет
1. Записать все процессы по созданию, составляющие моделируемы КПС в графу 2 таблицы 1, придерживаясь их хронологии.
2. В графе 3 для каждого процесса указать номера тех, процессов, которые непосредственно последуют за данным процессом.
3. В графе 1 для каждого процесса указать номера тех процессов, которые непосредственно предшествуют данному процессу.
4. Построить сетевой график процессов и связей между ними.
5. Проверить правильность (полноту) связей между процессами, исходя из содержательного смысла процесса. Для каждого процесса проверяется необходимость и достаточность всех непосредственно предшествующих.
6. Проверить правильность нумерации вершин и кодов дуг в СГП.
7. Преобразовать СГП в СГПС.
9. Проверить упрощенный СГПС на его соответствие СГП.
10. Пронумеровать вершины СГПС (рекомендуется использовать 5-шаговый алгоритм).
11. Составить табличный список процессов и событий моделируемого комплекса. В данной таблице записываются коды (I, j) процессов, в графе 2 – наименования процессов, в графе 3 – номера событий (вершин), в графе 4 – наименования событий.
12. Оформление отчета (при необходимости).
VII. Варианты оформления СГ.
Варианты оформления СГ могут отличаться по следующим признакам:
3. По размещению вершин на листе (направленность).
4. Наличие привязки к сетке:
5. Привязка СГ к шкале времени:
6. По расположению наименований (на сетевом графике).
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Генерация страницы за: 0.043 сек. —>
Алгоритм правильной нумерации.
Шаг 1. Нумеруем начальную вершину номером 1. Переходим к шагу 2.
Шаг 2. Удаляем из сети все выходящие из пронумерованных вершин дуги. Нумеруем в произвольном порядке вершины, в которые не входит ни одна дуга, произвольным образом возрастающими по порядку номерами. Шаг 2 проделываем до тех пор, пока не дойдем до конечной вершины, которой присваиваем следующий по порядку номер.
В результате правильной нумерации вершин сетевой график, приведенный на рис. 4 примет вид
Номера работ на дугах соответственно заменены продолжительностью их выполнения (продолжительность фиктивной работы соответствующей дуги-связи полагаем равной 0).
Рассмотрим основные временные параметры сетевого графика. Пусть tij –продолжительность работы, для которой соответствующая дуга (i, j) в сетевом графике имеет в качестве начальной – вершину с номером i , а в качестве конечной – вершину с номером j.
Ранним сроком начала работы (i, j) называется наименьшее допустимое время tij PH , когда может быть начато ее выполнение.
Если работа начата в ранний срок, то время ее окончания tij P 0 называется ранним сроком окончания
tij PН = tij PО —tij
Ранний срок начала всех работ, для которых вершина i – начальная, называется ранним сроком наступления события i и обозначается Ti P .
Ранний срок наступления конечного события называется критическим временем и обозначается Ткр. Таким образом, критическое время – это минимальный срок, за который может быть выполнен весь комплекс работ.
Каждый путь из начальной вершины в конечную, состоящий из дуг (работ) и дуг-связей продолжительностью Ткр, называется критическим путем, а работы, составляющие такие пути – критическими работами.
Поздними сроками начала и окончания работы (i, j) называется наибольшее допустимое время начала (tij ПН ) и окончания (tij П O ) этой работы без нарушения сроков выполнения всего комплекса работ. Очевидно:
tij ПН = tij ПО —tij.
Наиболее поздний из поздних сроков окончания работ, входящих в вершину j, называется поздним сроком наступления события j и обозначается Тj П .
Рассмотрим работу (i, j). Плановая продолжительность этой работы равна tij. Максимально допустимое время, на которое можно увеличить продолжительность работы (i, j) или задержать начало ее выполнения, при котором не изменится время выполнения всего проекта, называется полным резервом Rij времени этой работы. Он равен:
Rij = Tj П — Ti P – tij.
Резерв времени для работы (i, j), использование которого не изменит ранние сроки наступления всех событий (т.е. все работы смогут начать выполняться в минимально возможные сроки), называется свободным и может быть вычислен по формуле
rij = Tj P — Ti P – tij.
Очевидно, полный и свободный резерв времени любой работы, лежащей на критическом пути, равен нулю.
Алгоритм нахождения ранних сроков наступления событий
- Полагаем T1P= 0.
- Для j = 2, 3, . . . , n вычисляем TjP= (TkP+ tkj)
Здесь I(j) – множество всех дуг, входящих в вершину j. Критическое время Тkp=TnP .