3. Правила построения сетевых моделей
Единой последовательности построения сетевой модели (сетевого графика) нет. Поэтому строить модели можно по — разному — двигаясь от начала проекта (исходного события) к его окончанию (завершающему событию), и наоборот — от окончания к началу. Более логичным и правильным следует признать метод построения графиков от исходного события к завершающему, т.е. слева направо, так как при таком построении четко прослеживается технология выполнения моделируемых работ.
В качестве первого правила сетевого моделирования следует указать правило последовательности изображения работ: сетевые модели следует строить от начала к окончанию, т.е. слева направо.
Правило изображения стрелок. В сетевом графике стрелки, обозначающие работы, ожидания или зависимости, могут иметь различный наклон и длину, но должны идти слева направо, не отклоняясь влево от оси ординат, и всегда направляться от предшествующего события к последующему, т.е. от события с меньшим порядковым номером к событию с большим порядковым номером.
Правило пересечения стрелок. При построении сетевого графика следует избегать пересечения стрелок: чем меньше пересечений, тем нагляднее график.
Правило обозначения работ. В сетевом графике между обозначениями двух смежных событий может проходить только одна стрелка.
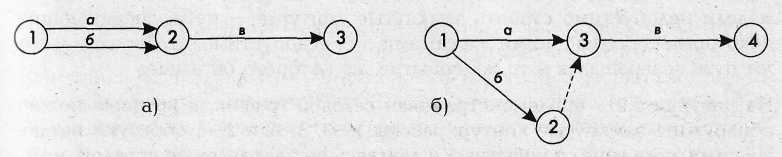
В практике зачастую встречаются случаи, когда две и более работы начинаются одним и тем же событием, выполняются параллельно и заканчиваются одним и тем же событием. Например, одновременно начинается проектирование двух вариантов конструкции новой машины (работы а и б), после чего проводится сопоставление и выбор лучшего варианта (работа в). Изображение этих работ на сетевом графике не должно выводить две работы из одного события и завершать их одним и тем же событием (рис. 6,а), так как в этом случае две работы получат одно и то же обозначение — 1—2. Это недопустимо, потому что при расчете сетевого графика невозможно будет определить параметры этих работ и параметры всего сетевого графика.
Для правильного изображения работ можно ввести дополнительное событие и зависимость (рис. 6,6). Теперь работы аиб имеют уникальные числовые обозначения — 1—3 и 1—2 соответственно, и никаких трудностей при расчете параметров сетевого графика не возникнет.
Рис. 6. Неверное изображение параллельно выполняемых работ (а), распараллеливание работ в сетевой модели (6)
Правило расчленения и запараллеливания работ. При построении сетевого графика можно начинать последующую работу, не ожидая полного завершения предшествующей. В этом случае нужно «расчленить» предшествующую работу на две, введя дополнительное событие в том месте предшествующей работы, где может начаться новая.
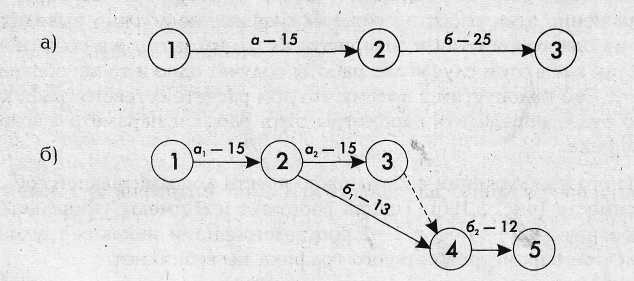
Например, необходимо корректировать рабочие чертежи (работа а, продолжительность 30 дней) и изготовить испытательный стенд (работа б, продолжительность 25 дней). Если эти работы изобразить последовательно, то их общая продолжительность составит 55 дней (рис. 7,а). Составив сетевой график и еще раз проанализировав взаимосвязи между работами, приходим к выводу, что работу б можно начать уже после того, как будет выполнена половина работы а, т.е. через 15 дней. Закончить же работу б можно только после полного завершения работы а. Исходя из этого, можно построить новый сетевой график (рис. 7,6). Как видно из рисунка, общая продолжительность работ теперь составляет 42 дня, т.е. получается выигрыш во времени продолжительностью в 13 дней.
Рис. 7. Последовательное изображение работ (а), расчленение и запараллеливание работ (б)
Правило запрещения замкнутых контуров (циклов, петель). В сетевой модели недопустимо строить замкнутые контуры — пути, соединяющие некоторые события с ними же самими, т.е. недопустимо, чтобы один и тот же путь возвращался в то же событие, из которого он вышел.
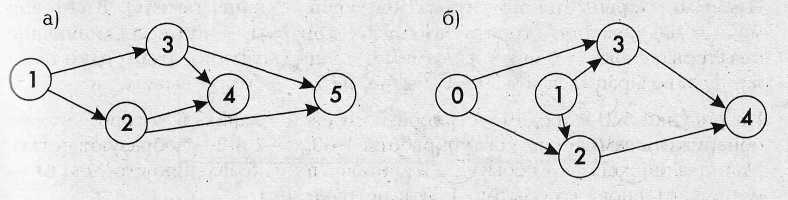
На рисунке 8,а продемонстрирован сетевой график, в котором можно обнаружить замкнутый контур: работы 1-—3, 3—2 и 2—1 образуют петлю. Начиная движение от события 1, и двигаясь по направлению стрелок, можно попасть снова к событию 1. Это недопустимо.
Рисунок 8,6 показывает, что при наличии пересечений обнаружить контуры труднее. Но, тем не менее, двигаясь по стрелкам, видим, что в данном случае замкнутый контур принял форму «восьмерки», объединяющей события 1, 3, 2 и 4: путь вернулся к исходному событию. Такое изображение также недопустимо.
Рис. 8. Неправильное построение сетевой модели: а) замкнутый контур в вице петли; 6) замкнутый контур
Если в модели образовался замкнутый контур, это значит, что имеются ошибки в технологии выполнения работ или в составлении графика (вспомните правило изображения стрелок).
Правило запрещения тупиков. В сетевом графике не должно быть тупиков, т.е. событий, из которых не выходит ни одна работа, за исключением завершающего события (в многоцелевых графиках завершающих событий несколько, но это особый случай) (рис. 9,а).
Правило запрещения хвостовых событий. В сетевом графике не должно быть хвостовых событий, т.е. событий, в которые не входит ни одна работа, за исключением начального события (рис. 9,6).
Рис. 9. Неправильное построение сетевой модели; а) наличие тупика; 6) наличие хвостового события
Правило изображения дифференцированно — зависимых работ. Если одна группа работ зависит от другой группы, но при этом одна или несколько работ имеют дополнительные зависимости или ограничения, при построении сетевого графика вводят дополнительные события.
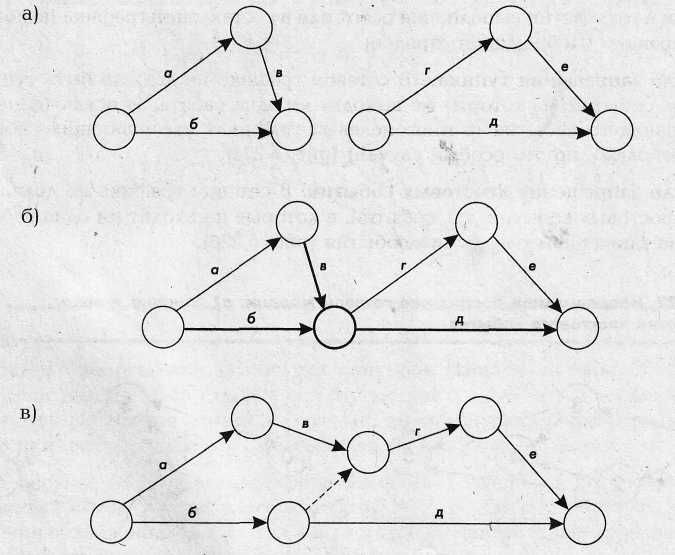
Допустим, есть две группы работ — а, б, в и г, д, е (рис. 10,а). Представим, что существует следующая зависимость между этими группами: работа г зависит от работ б и в, а работа д зависит только от работы б. Сетевая модель, объединяющая обе группы работ, которая приведена на рис. 10,6, не верна, так как сетевой график показывает, что работа д зависит как от работы б, так и от работы в, а это противоречит исходной моделируемой технологии.
Чтобы построить правильную сетевую модель, необходимо ввести дополнительное событие. Правильный сетевой график показан на рис. 10,в. В нем работы гид являются дифференцированно-зависимыми и каждая имеет свою зависимость от предшествующих работ.
Рис. 10. Две группы зависимых работ (а). Неправильное (б) и правильное (в) изображение зависимых работ в одной сетевой модели
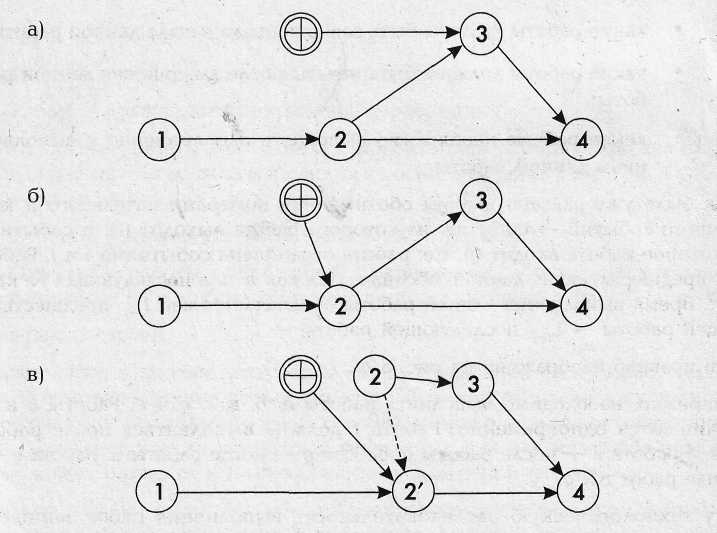
Правило изображения поставки. В сетевом графике поставки (под поставкой понимается любой результат, который предоставляется «со стороны», т.е. не является результатом работы непосредственного участника проекта) изображаются двойным кружком либо другим знаком, отличающимся от знака обычного события данного графика. Рядом с кружком поставки дается ссылка на документ (контракт или спецификацию), раскрывающий содержание и условия поставки.
Пример изображения поставки приведен на рис. 11,а. Но бывают и более сложные случаи.
Например, на рис. 11,6 показана поставка, входящая в событие 2. Судя по графику, поставка необходима сразу для двух работ — 2—3 и 2—4. Но если нужно изобразить, что поставка требуется для работы 2—4, следует применить правило изображения дифференцированно — зависимых работ, т.е. ввести дополнительное событие (2′) и зависимость (2—2′) (рис. 11,в). Поставка теперь необходима только для работы 2’—4, что соответствует производственной технологии.
Рис. 11. Изображение поставки: а) для одной работы; б) для двух работ; в) для одной из работ, выходящих из одного события
4. Использование календарей в MS Project.
Project позволяет использовать четыре типа календарей: базовые календари (Базовый календарь. Календарь, задающий стандартное рабочее и нерабочее время для набора ресурсов, который может использоваться в качестве календаря проекта или задачи. Отличается от календаря ресурса, задающего рабочее и нерабочее время для отдельного ресурса.), календари проектов (Календарь проекта. Базовый календарь, используемый в проекте.), календари ресурсов (Календарь ресурса. Календарь, задающий рабочее и нерабочее время для отдельного ресурса. Календарь ресурса отличается от базового календаря, задающего рабочее и нерабочее время для нескольких ресурсов.) и календари задач (Календарь задачи. Базовый календарь, который применяется при планировании отдельных задач, обычно независимый от календаря проекта и календарей назначенных ресурсов. По умолчанию все задачи планируются в соответствии с календарем проекта.). Они применяются для определения доступности ресурса, способа планирования ресурсов, назначенных для задач, и метода планирования задач. Для планирования задач используются календари проектов и календари задач, а если задачам назначены ресурсы, то могут использоваться также и календари ресурсов.
Эти календари можно изменять, определяя рабочие дни и часы для всего проекта, групп ресурсов, отдельных ресурсов и задач. Следует отличать вышеописанные календари от представления «Календарь», в котором показан план проекта в формате календаря.
Если в организации используется Microsoft Office Project Профессиональный 2007 и имеется подключение к Microsoft Office Project Server 2007, календари реализуются на сервере Project Server.
1. Основные понятия сетевой модели
Сетевая модель — графическое изображение плана выполнения комплекса работ, состоящего из нитей (работ) и узлов (событий), которые отражают логическую взаимосвязь всех операций. В основе сетевого моделирования лежит изображение планируемого комплекса работ в виде графа.
Граф — схема, состоящая из заданных точек (вершин), соединенных линиями. Отрезки, соединяющие вершины, называются ребрами (дугами) графа.
Ориентированным называется такой граф, на котором стрелкой указаны направления всех его ребер, что позволяет определить, какая из двух его граничных вершин является начальной, а какая — конечной. Исследование таких сетей проводится методами теории графов.
Теория графов оперирует понятием пути, объединяющим последовательность взаимосвязанных ребер. Контур означает такой путь, у которого начальная вершина совпадает с конечной. Сетевой график — это ориентированный граф без контуров. В сетевом моделировании имеются два основных элемента — работа и событие.
Работа — это активный процесс, требующий затрат ресурсов, либо пассивный (ожидание), приводящий к достижению намеченного результата.
Фиктивная работа — это связь между результатами работ (событиями), не требующая затрат времени и ресурсов.
Событие — это результат (промежуточный или конечный) выполнения одной или нескольких предшествующих работ.
Путь — это любая непрерывная последовательность (цель) работ и событий.
Критический путь — это путь, не имеющий резервов и включающий самые напряженные работы комплекса. Работы, расположенные на критическом пути, называют критическими. Все остальные работы являются некритическими (ненапряженными) и обладают резервами времени, которые позволяют передвигать сроки их выполнения, не влияя на общую продолжительность выполнения всего комплекса работ.
При построении сетевых моделей необходимо соблюдать следующие правила.
- Сеть изображается слева направо, и каждое событие с большим порядковым номером изображается правее предыдущего. Общее направление стрелок, изображающих работы, также в основном должно быть расположено слева направо, при этом каждая работа должна выходить из события с меньшим номером и входить в событие с большим номером.
- Два соседних события могут объединяться лишь одной работой. Для изображения параллельных работ вводятся промежуточное событие и фиктивная работа (рис. 27-1).
- В сети не должно быть тупиков, т.е. промежуточных событий, из которых не выходит ни одна работа (рис. 27.2).
- В сети не должно быть промежуточных событий, которым не предшествует хотя бы одна работа (рис. 27.3).
- В сети не должно быть замкнутых контуров, состоящих из взаимосвязанных работ, создающих замкнутую цепь (рис. 27.4).
Для правильной нумерации событий поступают следующим образом: нумерация событий начинается с исходного события, которому дается номер 1. Из исходного события 1 вычеркивают все исходящие из него работы, на оставшейся сети вновь находят событие, в которое не входит ни одна работа. Этому событию дается номер 2. Затем вычеркивают работы, выходящие из события 2, и вновь находят на оставшейся части сети событие, в которое не входит ни одна работа, ему присваивается номер 3, и так продолжается до завершающего события. Продолжительность выполнения работ устанавливается на сновании действующих нормативов или по экспертным оценкам специалистов. В первом случае временные оценки являются детерминированными (однозначными), во втором — стохастическими (вероятностными).