5 Табличный метод расчета параметров сетевой модели
Принципиальное отличие табличного метода от графического заключается в том, что он позволяет рассчитать параметры сетевой модели непосредственно в таблице, в которую предварительно заносятся в определенном порядке все работы и их продолжительность.
ранний срок начала работы — tpнij;
ранний срок окончания работы — tpojj;
поздний срок начала работы – tnнij;
поздний срок окончания работы — tnоij;
частный резерв первого вида – Р’nij,
частный резерв второго вида – Р”nij.
На основе производственного расчета параметров сети определяется критический путь сетевой модели и его продолжительность.
Ниже приводятся правила для определения параметров сети.
Правило 1. Для определения времени первого начала данной работы tрнij рассматриваются все работы, входящие в начальное событие данной работы. Из графы tро входящих работ выбирается максимальное время раннего окончания (tро)max, которое переносится в графу tрнij данной работы.
Правило 2. Время раннего окончания работы tpojj равно времени раннего начала этой работы плюс ее продолжительность:
Правило 3. Для нахождения времени позднего окончания данной работы tnоij рассматриваются все работы, выходящие из конечного события данной работы. Из графы tnн выходящих работ выбирается минимальное время позднего начала (tnн)min, которое переносится в графу tnо данной работы (расчет ведется снизу вверх).
Если в завершающее событие входят две или несколько работ, то время окончания этих работ определяется максимальным значением их раннего окончания.
Правило 4. Время позднего начала данной работы tnнij равно времени позднего окончания этой работы tnoij минус ее продолжительность :
Правило 5. Полный резерв времени работы Рnij определяется разностью между поздним началом этой работы:
либо разностью между поздним и ранним окончанием этой работы:
Правило 6. Для определения частного резерва первого вида данной работы Р’nij рассматриваются работы, имеющие то же начальное событие. Из графы tnн этих работ выбирают минимальное время позднего начала, которое вычитается из времени начала данной работы.
Если из события выходит одна работа, то частный резерв первого вида этой работы равен 0.
Правило 7. Для определения частного резерва времени второго вида данной работы Р”nij рассматриваются работы, имеющие одинаковые конечные события. Из графы tpo этих работ выбирается максимальное время раннего окончания, из которого вычитают время раннего окончания данной работы.
Если в событие входит одна работа, то частный резерв времени второго вида этой работы равен 0.
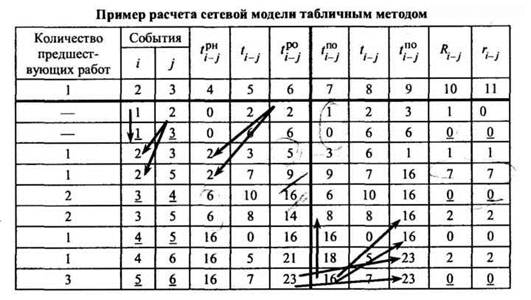
Произведем расчет представленной на рисунок 16 сетевой модели с помощью приведенных выше правил. Продолжительность работ указана в неделях.
Указанные выше параметры сети определяются в следующем порядке.
1 этап. По данным сетевой модели заполняются графы 2,3,1 и 4 таблица 1. В графу 1 записывается количество работ, непосредственно входящих в начальное событие данной работы.
После заполнения указанных граф весь расчет ведется в таблице без использования сетевой модели.
2 этап. Определяется раннее начало и окончание работ, т.е. заполняются графы 5 и 6 таблица1. Раннее начало работ с начальным событием, являющимся в то же время исходным событием данной сетевой модели, принимается равным нулю: tpнij = 0.
Кол-во предшествующих работ
Продолжит. работы в неделях
Методы расчета сетевых моделей
Расчет сетевой модели заключается в определении его параметров, к которым относятся:
— раннее начало каждой работы — самый ранний срок, когда может быть начата данная работа;
— раннее окончание каждой работы — самый ранний срок, когда может быть завершена данная работа;
— позднее начало каждой работы — самый поздний срок, когда может быть начата данная работа (при условии, что все работы будут завершены к установленному сроку);
— позднее окончание каждой работы — самый поздний срок, когда может быть окончена данная работа (при условии, что все работы будут завершены к установленному сроку);
— полный резерв времени каждой работы — запас времени, которым располагает каждая работа (при условии, что все работы будут завершены к установленному сроку);
— частный резерв времени каждой работы — запас времени, которым располагает каждая работа при условии, что все последующие работы начнутся в ранние сроки. Это резерв времени работ каждой ветви сетевой модели, рассматриваемой в качестве самостоятельной (частной) модели.
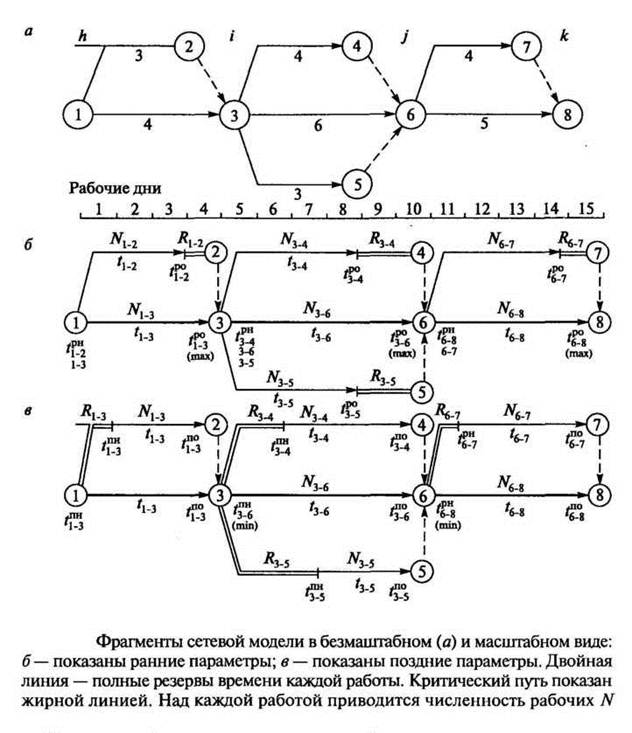
Рассмотрим фрагмент сетевой модели приведенной в масштабный вид, с выполнением работ в ранние (б) и поздние (в) сроки.
 |
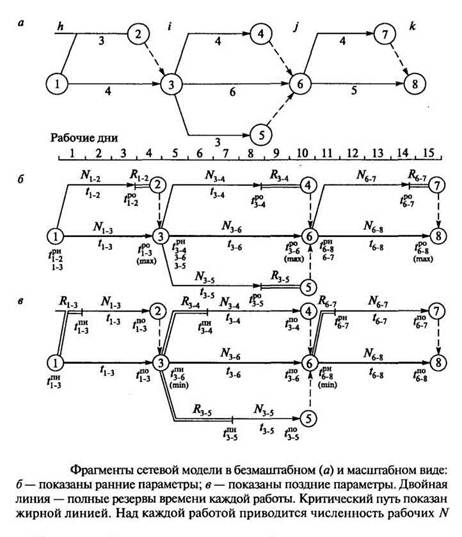 |
Критический путь проходит по тем работам, для которых
Существуют несколько методов расчета: аналитический, табличный, секторный, потенциалов, матричный и другие.
Наиболее распространенными из них являются:
— табличный (модернизированный аналити ческий
Табличный метод является наиболее универсальным, им могут быть рассчитаны сетевые модели с любым количеством событий, в расчете использована современная вычислительная техника.
 |
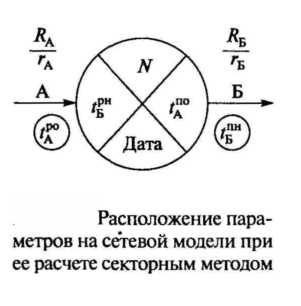
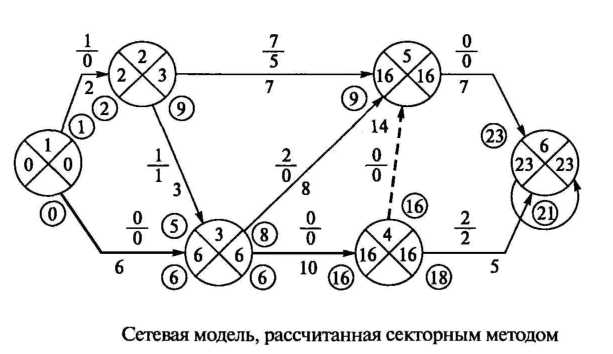
Секторный метод расчета применяют при расчете сетевых моделей с сравнительно небольшим количеством событий. Расчет выполняют непосредственно на модели.
Размещение параметров в секторах и на самой модели приведено на рисунке.
Методическая основа расчета та же, что и при табличном методе — используют те же расчетные формулы.
Последовательность расчета — ранние сроки считают слева направо, для последнего события переносят значение tрн i -j из левого сектора в правый tпо i -j и ведут расчет поздних параметров в обратном порядке — справа налево. Значение резервов записывают над каждой работой.
 |
Параметры сетевых моделей и методы их расчета
Сетевая модель имеет ряд характеристик, которые позволяют определить степень напряженности выполнения отдельных работ, а также всего их комплекса и принять решение о перераспределении ресурсов.
Ранний срок наступления события tр(i) — самый ранний из возможных сроков наступления события. Он равен продолжительности максимального пути от исходного события до данного.
tр(i) = max t[Lр(i)] (2.1)
Например, tр(7)=19, т.к. L1=(1,2,4,7), L2=(1,3,4,7),
t(L1)=5+12=17 < t(L2)=7+12=19.
Ранний срок начала работы tр.н.(i,j) равен продолжительности максимального пути от исходного до начального события данной работы.
tр.н.(i,j)=max t[Ln(i)](2.2)
Например, tр.н.(7,11)=19, т.к. L1=(1,2,4,7), L2=(1,3,4,7),
t(L1)=5+12=17
Ранний срок начала работы равен раннему сроку наступления начального события данной работы.
tр.н.(i,j) = tр(i) (2.3)
Ранний срок окончания работы tр.о.( i,j) равен сумме раннего срока начала работы и продолжительности данной работы.
tр.о.(i,j)= tр.н.(i,j) + t(i,j) (2.4)
Например, tр.о.(7,11)= tр.н.(7,11) + t(7,11)= 19+8=27.
Поздний срок наступления события tп( i) равен разности между продолжительностью критического пути и продолжительностью максимального пути от данного события до завершающего.
tп(i) =Tкр — max t[Lк(i)](2.5)
Например, tп(7)=19, т.к. L1=(7,11), L2=(7,9,11), t(L1)=8 > t(L2)=4,
tп(7) = Tкр — max t[Lк(7)]=27 — 8=19.
Для событий критического пути tр( i)=tп(i), для других событий tр(i)tп(i).
Поздний срок окончания работы tп.о.( i,j) – это самый поздний срок окончания работы, при котором планируемый срок окончания проекта не меняется, он равен разности между продолжительностью критического пути и продолжительностью максимального пути от конечного события данной работы до завершающего события.
tп.о.(i,j)=Tкр — max t[Lк(j)] (2.6)
Поздний срок окончания работы равен позднему сроку наступления конечного события tп.о.(i,j) = tп(j). Например, tп.о.(4,7) = tп(7)=19.
Поздний срок начала работы tп.н.( i,j) – самый поздний срок начала работы, при котором планируемый срок окончания проекта не меняется.
tп.н.(i,j)= tп .о.(i,j) — t(i,j) (2.7)
Например, tп.н.(4,7)= tп.о.(4,7) — t(4,7)=19-12=7.
Для работ критического пути ранние и поздние сроки начала и окончания работ равны: tр.н.(4,7)= tп.н.(4,7)=7, tр.о.(4,7)= tп.о.(4,7)=19.
Работы, не лежащие на критическом пути, могут иметь резервы времени.
Полный резерв времени Rп( i,j) – максимальное время, на которое можно увеличить продолжительность данной работы, не изменяя продолжительности критического пути.
Rп (i,j)= tп(j) — tр(i) — t(i,j)
Rп(i,j)= tп.н (i,j) — tр.н.(i,j) (2.8)
Rп (i,j)= tп.о.(i,j) — tр.о.(i,j)
Свободный резерв времени Rс( i,j) равен разности между ранним началом последующей работы и ранним окончанием рассматриваемой работы.
Rс(i,j)= tр.н (j,к) — tр.о.(i,j) (2.9) Перейти к онлайн решению своей задачи