5.5.Пример оптимизации сетевой модели по трудовым
Основным методом решения этой задачи является сдвиг части работ из положения, соответствующего наиболее раннему времени их начала, на более позднее время в пределах полного резерва. Задача оптимизация сводится к составлению такого расписания работ, которое обеспечивало бы наибольшую равномерность графика трудовых ресурсов.
Для решения задачи оптимизации сетевой модели предстоит построить ее линейную диаграмму. Для этого проводят две оси – горизонтальную и вертикальную. Горизонтальную ось делят на равные отрезки, количество которых равно числу дней критического пути рассматриваемой модели. Вертикальную ось делят на количество отрезков, равное числу работ сетевой модели с учетом фиктивных работ. После этого на линейную диаграмму наносят все работы сетевой модели в виде линий, изображенных в масштабе времени.
Фиктивные работы изображаются в виде точек.
При этом необходимо руководствоваться следующими правилами:
а) все работы должны быть размещены на линейной диаграмме в положении наиболее раннего времени начала;
б) построение линейной диаграммы начинается снизу вверх, в порядке возрастания номеров начальных событий для работ.
При этом если из событий выходят несколько работ, то они располагаются в порядке возрастания полных резервов времени.
Работы на линейной диаграмме имеют ту же нумерацию, что и на сетевой модели.
Над каждой работой указывается численность персонала для ее выполнения.
По линейной диаграмме подсчитывается ежедневная суммарная численность исполнителей (Ni), которая записывается по соответствующим дням в горизонтальной строке под линейной диаграммой.
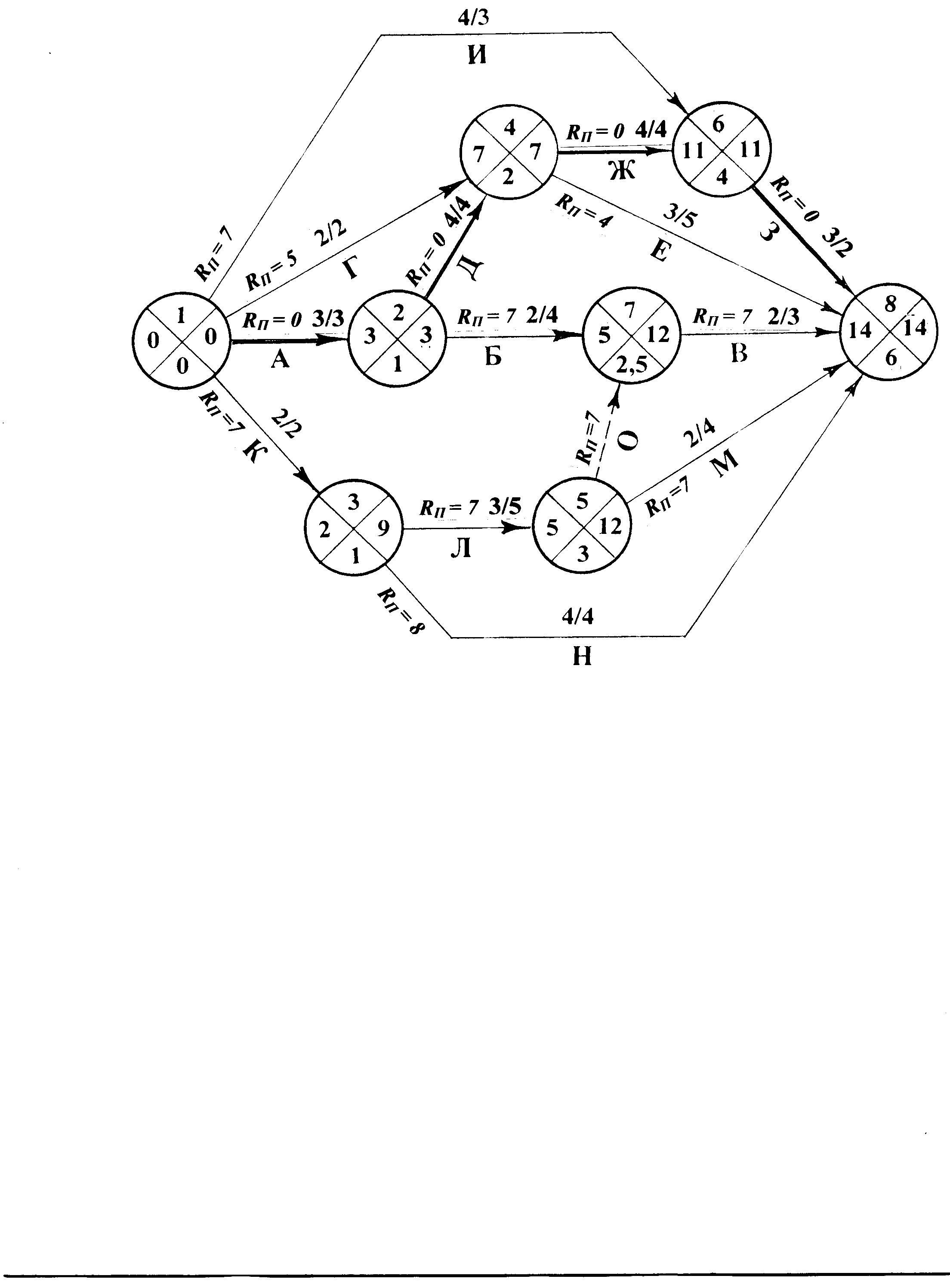
Рассмотрим пример построения линейной диаграммы и порядок выполнения оптимизации для сетевой модели, изображенной на рис.5.4. Модель рассчитана и приведена к директивной продолжительности, т.е. Ткр = Тд = 14 дней.
Рис 5.4. Приведенный сетевой график ремонта узла
до оптимизации по ресурсам
Построение линейной диаграммы (рис.5.5) начинается с деления горизонтальной оси на 14 отрезков, так как Ткр = 14. Вертикальная ось делится на 14 отрезков, так как число работ сетевой модели – 14.
Рассматриваются работы, выходящие из первого события. К ним относятся четыре работы – 1,2; 1,3; 1,4; 1,6. Их полные резервы соответственно равны: работы 1,2 — 0; 1,3 — 7; 1,4 — 5; 1,6 — 7.
Рис.5.5. Линейная диаграмма ремонта
Работы на линейной диаграмме располагаются в очередности возрастания резервов. Если резервы работ одинаковы, сначала располагают работу с наименьшим последующим событием. Аналогично, руководствуясь ранее приведенными правилами, строятся на линейной диаграмме все остальные работы сетевой модели. Затем подсчитывается суммарная численность персонала по дням ремонта путем сложения численности исполнителей работ, выполняемых в рассматриваемый день, и результаты записываются в строке под горизонтальной осью линейной диаграммы.
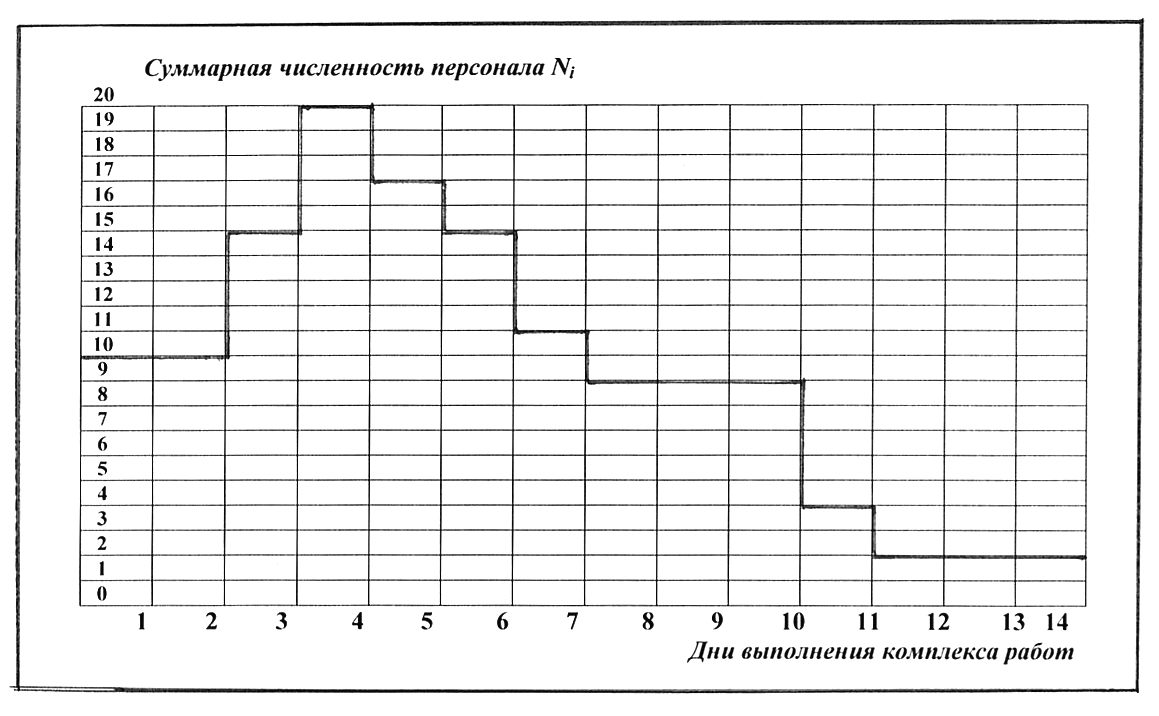
По результатам расчета суммарной численности можно построить график потребности трудовых ресурсов по дням (рис.5.6.).
Рис.5.6. График потребности трудовых ресурсов по дням
Как видно из рис.5.6., график суммарной численности неравномерен.
Проверку целесообразности сдвига работ с целью выравнивания графика потребности трудовых ресурсов необходимо начать с верхней работы линейной диаграммы, переходя последовательно вниз до самой нижней.
Целесообразность сдвига работ устанавливается расчетом «столбцов нарастающих сумм».
Рассмотрим этот расчет на примере проверки целесообразности сдвига работы 7,8 на линейной диаграмме, изображенной на рис.5.5.
Для большей наглядности воспроизводим линейную диаграмму с результатами подсчета суммарной численности персонала, но с изображением одной работы 7,8, полный резерв которой равен 7 (рис. 5.7.).
Предельное положение работы при ее перемещении вправо отмечаем крестиком на линейной диаграмме.
Последовательность формирования столбцов нарастающих сумм приводится ниже.
Составляется первый столбец из суммарной численности персонала в дни резерва работы 7,8
Составляется второй столбец из суммарной численности персонала, начиная с первого дня исходного положения работы без численности исполнителей данной работы до заполнения всех строк первого столбца.
Составляется третий столбец из разности значений численности первого и второго столбца каждой строки.
Составляется четвертый (последний) столбец – столбец нарастающих сумм.
В первую строчку четвертого столбца вносится значение первой строчки третьего столбца, во вторую строчку — алгебраическая сумма чисел, записанных в первой строчке четвертого столбца и второй строчки третьего столбца и т.д. до заполнения всех строчек.
Решение вопроса о целесообразности сдвига работы можно получить путем анализа величин, записанных в четвертом столбце. Если в четвертом столбце все цифры положительные, то сдвиг данной работы нецелесообразен. Если же в нем окажутся отрицательные величины, то необходимо зафиксировать отрицательное число с наибольшей абсолютной величиной и определить порядковый номер строки, в которой это число появилось первый раз. Рассматриваемую работу целесообразно сдвинуть вправо на количество дней, равное порядковому номеру данной строки. Так, в приведенном примере отрицательное число с наибольшей абсолютной величиной (-16) впервые появляется в шестой строке четвертого столбца, поэтому работу 7,8 сдвигаем на 6 дней.
В соответствии с этим сдвигом производим корректировку суммарной численности персонала в дни исходного и нового положений работы. Равномерность численности персонала не изменится, если работу передвинуть на 7 дней, что соответствует седьмой строчке, в которой вторично появляется число – 16. При этом вопрос о целесообразности сдвига работ решается путем дополнительного анализа, так как результатом сдвига явится с одной стороны уменьшение резерва, с другой – более широкие возможности для дальнейшей оптимизации ресурсов, так как сдвиг работ с частичным использованием полного резерва уменьшает возможности сдвига предшествующих работ на эту величину.
Оптимизация сетевой модели (рис.5.4) в целом по численности персонала показана на линейной диаграмме (рис. 5.8).
Проверка целесообразности сдвига работы 7,8, описанная выше, производится вторично.
Работу сдвигаем на 6 дней
не рассматривается, так как она фиктивная и не имеет ресурсов, ее положение определяется непосредственно следующей работой
После окончания описанного этапа оптимизации (первого шага) следует сделать «второй шаг оптимизации» аналогично первому на той же линейной диаграмме. Как правило, оптимизация завершается на втором шаге, реже на третьем.
После проведения оптимизации сетевых моделей методом сдвига работ в большинстве случаев наблюдается значительное выравнивание численности исполнителей по дням выполнения комплекса работ. Так, на рис.5.6 при-
Рис.5.8. Линейная диаграмма ремонта.
веден график распределения трудовых ресурсов до оптимизации сетевой модели, а на рис.5.9 – после оптимизации. Результаты оптимизации очевидны, но не вполне удовлетворительны.
Рис.5.9. График потребности трудовых ресурсов по дням
после первого шага оптимизации.
Если исчерпаны все возможности оптимизации методом сдвига работ, но при этом результаты оптимизации не совсем удовлетворительны, то нужно применить дополнительные методы выравнивания:
а) перевод некоторых работ в ускоренный или замедленный режим;
б) выполнение работ по частям;
в) выполнение работ по частям в ускоренном или замедленном режиме.
Сдвиги работ, полученные в процессе оптимизации трудовых ресурсов на линейной диаграмме, вносятся в сетевую модель. Для этого просмотром линейной диаграммы снизу вверх определяется сдвиг в днях начала непосредственно следующей работы относительно окончания непосредственно предшествующей работы. Именно этот сдвиг вносится в сетевую модель, отражая организационное ожидание для данной работы. Сам по себе сдвиг работы относительно раннего времени ее начала не свидетельствует о наличии организационного ожидания, равного сдвигу работы. Например, в рассматриваемой линейной диаграмме (рис.5.8) работа 5,8 сдвинута вправо относительно раннего времени начала на 7 дней, но организационное ожидание ее равно 5 дням, так как непосредственно предшествующая работа 3,5 сдвинута вправо на 2 дня и разрыв по времени между окончанием работы 3,5 и началом работы 5,8 равен 5 дням.
Рис.5.10. Приведенный сетевой график ремонта узла после
первого шага оптимизации по ресурсам
Величины организационных ожиданий записываются на флажках, стоящих у начала работ. С учетом указанных на флажках значений ожиданий сетевая модель пересчитывается и определяются новые значения tp(i) = = tn(i) для всех событий, выявляется новый критический путь (или новые критические пути). Ранее время начала работ с предшествующим организационным ожиданием определится как ранее время совершения начального события этой работы плюс значение ожидания, указанное на флажках работы. После корректировки график приобретает вид, изображенный на рис. 5.10. Такой график может быть календаризирован и принят к исполнению в качестве оперативного плана работ.
3.3.2. Пример проведения оптимизации сетевой модели по критерию «Время — затраты»
Проведем максимально возможное уменьшение сроков выполнения проекта при минимально возможных дополнительных затратах для следующих исходных данных (табл.3.1, рис. 3.2).
Исходные данные для оптимизации «Время -затраты»
Рис.3.2. Исходная сетевая модель
Исходя из нормальных длительностей работ получаем следующие характеристики сетевой модели.
- Общие затраты на проект руб.
- Длительность проекта дней.
- Критический путь или .
- Подкритический путь или , дней.
Кроме того, вычислим коэффициенты нарастания затрат и максимальные запасы времени сокращения работ сетевой модели (табл. 3.2).
Коэффициенты нарастания затрат работ сети
I шаг. Для сокращения выбираем критическую работу с минимальным коэффициентом руб./день. Текущий запас сокращения времени работы на данном шаге равен дня. Разность между продолжительностью критического и подкритического путей дня. Поэтому согласно п.3.2 описанной выше общей схеме оптимизации сокращаем работу на дня. Новая текущая длительность работы дня, а запас ее дальнейшего сокращения сокращается до дня. Измененный сетевой график представлен на рис.3.3
Рис.3.3. Сетевая модель после первого шага оптимизации
После ускорения работы возникли следующие изменения.
- Затраты на работу возросли на и общие затраты на проект составили руб.
- Длительность проекта дней.
- Критические пути и .
- Подкритический путь , дней.
II шаг. Одновременное сокращение двух критических путей можно провести либо ускорив работу , принадлежащую обоим путям, либо одновременно ускорив различные работы из каждого пути. Наиболее дешевым вариантом является ускорение работ и — 1,60 руб./день за обе работы, тогда как ускорение работы обошлось бы в 7 руб./день. Поскольку , то сокращаем работы и на день. Запасы дальнейшего сокращения времени работ сокращаются до и дней. Измененный сетевой график представлен на рис.3.4.
Рис.3.4. Сетевая модель после второго шага оптимизации
После ускорения работ и возникли следующие изменения.
III шаг. Поскольку на данном шаге работа исчерпала свой запас ускорения, то наиболее дешевым вариантом сокращения обоих критических путей является ускорение работ и — 2,60 руб./день за обе работы. Сокращаем работы и на дня. Запасы дальнейшего сокращения времени работ и обнуляются. Измененный сетевой график представлен на рис.3.5.
Рис.3.5. Сетевая модель после третьего шага оптимизации
После ускорения работ и возникли следующие изменения.
IV шаг. Поскольку кроме работы все остальные работы критического пути исчерпали свой запас времени ускорения, то единственно возможным вариантом сокращения обоих критических путей является ускорение работы . Сокращаем работу на дня. Запас дальнейшего сокращения времени работы обнуляется. Измененный сетевой график представлен на рис.3.6.
Рис.3.6. Сетевая модель после четвертого шага оптимизации
После ускорения работы возникли следующие изменения.
- Общие затраты на проект составили руб.
- Длительность проекта дней.
- Три критических пути , и .
- Подкритические пути отсутствуют.
Дальнейшая оптимизация стала невозможной, поскольку все работы критического пути исчерпали свой запас времени ускорения, а значит проект не может быть выполнен меньше, чем за дней.
Таким образом, при отсутствии ограничений на затраты минимально возможная длительность проекта составляет 7 дней. Сокращение длительности проекта с 16 до 7 дней потребовало 28,00 рублей прямых затрат. В отличие от прямых затрат при уменьшении продолжительности проекта косвенные затраты ( руб./день) убывают, что показано на графике (см. рис.3.7). Минимум общих затрат (точка А) соответствует продолжительности проекта 14 дней.
Если же учитывать ограничение по средствам, выделенным на выполнение проекта, рубля, то оптимальным является выполнение проекта за 9 дней (точка B).