Пример сетевая модель управления

Сетевые модели управления

Основные элементы сетевого планирования и управления

Сетевое планирование и управление – это структура расчетных методов, включающая организационные и контрольные мероприятия, направленные на планирование и управление комплексом работ посредством сетевых графиков, то есть сетевых моделей.

Комплекс работ – это любая задача, для выполнения которой должно быть осуществлено большое количество разного рода работ.

Чтобы составить план работ по осуществлению больших и сложных проектов, включающих несколько тысяч отдельных исследований и операций, необходимо составить его описание посредством определенной математической модели. Такое средство описания проекта – модель.

Сетевая модель – это план выполнения определенного комплекса взаимосвязанных работ, заданный как сеть, графическое изображение которой – сетевой график.

Главные элементы сетевой модели: работы и события

Под работой в сетевой модели управления понимают:

• настоящую работу, то есть процесс напряжения и ресурсных затрат, занимающий определенный промежуток времени. Любую действительную работу отличает конкретность, четкое описание и наличие ответственного исполнителя;
• ожидание – процесс, растянутый во времени, не требующий трудовых затрат, например, сушка изделия после покраски;
• зависимость, или фиктивная работа – предполагает логическую связь двух или нескольких типов работ, не требующих трудовых затрат, материальных ресурсов или времени. Она демонстрирует зависимость возможности одной работы от результатов другой.

Событие – это момент завершения какого-то рассматриваемого процесса, в котором отражена отдельная ступень выполнения проекта.

Событие может выступать как частный результат отдельной работы или суммарный результат нескольких работ. Событие считается завершенным только после завершения всех предшествующих работ. Последующие работы начинаются только после свершения события.

Этим объясняется двойственный характер любого события: для всех работ, непосредственно предшествующих событию, оно является конечным, а для следующих за ним – начальным.

Среди событий сетевой модели принято выделять исходное и завершающее. Исходное событие не предполагает наличия предшествующих событий и работ, которые бы относились к представленному в модели комплексу работ. У завершающего события отсутствуют последующие работы и события.

Известен также принципиально другой принцип построения сетей – без событий. В таком случае вершинами графика будут определенные работы, а стрелками – зависимости между работами, которыми определяется порядок их выполнения.

Сети без событий существенно более громоздкие, так как обычно событий меньше, чем работ, а это выступает показателем сложности сети, равным отношению числа работ к числу событий, и обычно больше единицы. В связи с этим данный тип сетей менее эффективен с точки зрения управления целостным комплексом.

Если в сетевой модели отсутствуют числовые оценки, то такая сеть – структурная. Но на практике чаще всего используют сети, в которых задаются оценки продолжительности работ, а также оценки других параметров, например, трудоемкость, стоимость и пр.

Порядок и правила построения сетевых графиков

Сетевые графики составляют на начальной стадии планирования. Изначально планируемый процесс разбивают на несколько отдельных работ, составляют перечень событий и работ, продумывают логические связи между ними и последовательность выполнения, работы закрепляют за ответственными исполнителями. С помощью них, а также нормативов, если они есть, оценивают продолжительность каждого типа работ. Затем составляют сетевой график. После того, как сетевой график упорядочен, начинают рассчитывать параметры событий и работ, определять временные резервы и критические пути. На последок проводят анализ и оптимизацию сетевого графика, который в случае необходимости может быть вычерчен заново с пересчетом параметров событий и работ.

В процессе построения сетевого графика соблюдают некоторые правила:

• в сетевой модели должны отсутствовать «тупиковые» события, то есть события, из которых не выходит ни одной работы, кроме завершающего события. В таком случае работа или не нужна, или должна быть аннулирована, либо не отмечена необходимость проведения определенного типа работы, следующей за событием, чтобы свершить какое-либо последующее событие. В таком случае необходимо тщательно изучить взаимосвязи событий и работ, чтобы исправить возникшую неточность;
• в сетевом графике должны отсутствовать «хвостовые» события, кроме исходного, которым не предшествует ни одной работы. Если в сети есть такие события, следует заняться определением исполнителей предшествующих им работ и включить эти работы в структуру сети;
• в сети должны отсутствовать замкнутые контуры и петли, то есть пути, соединяющие некоторые события с ними же самими. Если отмечено возникновение контура, что можно обнаружить в сложных сетях с высокой сложностью достаточно часто, только с помощью ЭВМ. В таком случае следует вернуться к исходным данным и через пересмотр состава работ добиться его устранения;
• любые два события должны быть непосредственно связаны не более чем одной работой-стрелкой. Нарушение такого условия происходит с изображением параллельно выполняемых работ. Если эти работы оставить без изменения, то возможно возникновение путаницы, вызванной тем, что два разных типа работ имеют одинаковое обозначение. При этом содержание этих работ, состав привлекаемых исполнителей и количество ресурсов, затраченных на работу могут существенно отличаться;
• в сети рекомендуется иметь одно исходное и одно завершающее событие. Если в составленной сети данное требование не соблюдено, то исправить это моно через введение фиктивных работ и событий.

Если у сети есть одна конечная цель, то программа – одноцелевая. Сетевой график, в котором отмечено несколько завершающих событий, — многоцелевой и расчет ведется относительно каждой из конечных целей. Например, строительство жилого микрорайона, где ввод в эксплуатацию каждого отдельного дома – конечный результат, и в графике по возведению каждого дома определен свой критический путь.

Источник

16. Сетевые модели управления программами.

Сетевые модели наиболее широко используются в управлении проектами. Сетевая модель отображает комплекс работ (операций) и событий и их взаимосвязь во времени. Обычно сетевая модель предназначена для выполнения работ в такой последовательности, чтобы сроки выполнения проекта были минимальными. В этом случае ставится задача нахождения критического пути. Однако существуют и такие сетевые модели, которые ориентированы не на критерий времени, а, например, на минимизацию стоимости работ.

Сетевая модель.

Сетевая модель отображает взаимосвязи между операциями и порядок их выполнения.

Для представления операции используется стрелка, направление которой соответствует процессу реализации программы во времени.

Отношение упорядочения между операциями задается с помощью событий. Событие определяется как момент времени, когда завершаются одни операции и начинаются другие.

Начальная и конечная точка любой операции описываются, таким образом, парой событий, которые обычно называют начальным событием и конечным событием.

Операции, выходящие из некоторого события, не могут начинаться, пока не будут завершены все операции, входящие в это событие.

Каждое событие — это узел(вершина), а каждая операция — это ориентированная дуга.

Типичный пример графического изображения операции i, j с начальным событием i и конечным событием j.

Другой пример, из которого видно, что для возможности начала операции (3,4) требуется завершение операций (1,3) и (2,3).

Протекание операций во времени задается путем нумерации событий, причем номер начального события всегда меньше номера конечного.

17. Правила построения сетевого графика

Обычно сетевой график строится от исходного события к завершающему, слева направо, то есть каждое последующее событие изображается несколько правее предыдущего.

В планируемых процессах часто встречаются сложные комплексные связи, когда две или более работ выполняются параллельно, но имеют общее конечное событие, или когда для выполнения одной из работ необходимо предварительно выполнить несколько работ, а для другой, выходящей из общего для них события, предварительным условием является выполнение только одной из предшествующих работ и т.д. Изображение в сетевой модели подобных параллельных или дифференцированно зависимых работ выполняется следующим образом.

В случае, когда наступление события (например, 3 на рис. 14.2) возможно в результате завершения двух работ и , но в то же время существует событие 4 (рис. 14.2), зависящее от завершения только одной из этих работ (например, ), вводится фиктивная работа (см. рис. 14.2).

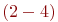
Если одно событие (например, 1 на рис. 14.3) служит началом двух (например, и или нескольких работ, заканчивающихся в другом событии (3 на рис. 14.3)), то для их различия также вводится фиктивная работа (см. рис. 14.3). С помощью фиктивной работы в сетевом графике могут быть отражены и двусторонние связи (зависимости).

Пусть, например, имеются три процесса . При этом окончание процесса зависит от результатов процессов и . В этом случае возникают двусторонние зависимости, которые можно изобразить так, как показано на (рис. 14.4).

Другое правило построения сетевого графика заключается в том, что если несколько работ может начаться не после полного, а после частичного выполнения определенной работы, то последнюю работу целесообразно представить как сумму ее частей, расчлененных событиями ( , , , и на рис. 14.5). И в то же время, группу работ целесообразно представить одной работой, если в этой группе имеется по одному начальному и конечному событию ( и на рис. 14.6).

Для отображения времени и места поступления дополнительных ресурсов (например, пополнение личного состава, топлива и т.д.) и другой информации на сетевом графике закрашенным кружком изображаются так называемые подставки (рис. 14.7). При наличии двух и более работ, выходящих из события, с которым необходимо связать подставку, последняя соединяется с дополнительно введенным событием через фиктивную работу (рис. 14.7).

После построения сетевого графика проверяется отсутствие работ, имеющих одинаковые коды. При наличии таких работ вводятся дополнительные события и фиктивные работы. Кроме того, сетевой график должен содержать только одно исходное событие и только одно завершающее событие.

Если эти условия не выполнены, то необходимо добавить еще одно исходное событие и соединить его стрелками с имеющимися несколькими начальными событиями или добавить еще одно конечное событие, к которому ведут стрелки от нескольких имеющихся конечных событий.

Сетевой график не должен иметь циклов, то есть таких путей, в которых конец последней работы совпадает с началом первой работы. Сетевой график, имеющий хотя бы один цикл, не может быть реализован, так как ни одна из работ, входящих в такой цикл, никогда не может начаться.

Источник