Примеры построения сетевых моделей

Пример построения сетевого графика

Используя полученные данные, мы можем найти основные характеристики сетевой модели табличным методом, критический путь и его продолжительность.
Таблица – Табличный метод расчета сетевого графика.

КПР	Код работы (i,j)	Продолжительность работы t(i, j)	Ранние сроки		Поздние сроки		Резервы времени
			tрн(i,j)	tро(i,j)	tпн(i,j)	tпо(i,j)	Rп	Rc
1	2	3	4	5	6	7	8	9
0	1,2	7	0	7	0	7	0	0
0	1,4	4	0	4	17	21	17	8
0	1,5	3	0	3	19	22	19	0
1	2,3	3	7	10	7	10	0	0
1	2,8	13	7	20	19	32	12	12
1	3,4	2	10	12	19	21	9	0
1	3,6	13	10	23	10	23	0	0
2	4,7	5	12	17	21	26	9	0
1	5,7	4	3	7	22	26	19	10
1	6,8	9	23	32	23	32	0	0
2	7,8	6	17	23	26	32	9	9

Таким образом, работы критического пути (1,2),(2,3),(3,6),(6,8). Продолжительность критического пути Т_кр=32.

Рисунок — Масштабный график сетевой модели
Для оценки вероятности выполнения всего комплекса работ за 30 дней нам необходима следующая формула: P(t_кр где Z=(Т-Т_кр)/S_кр
Z- нормативное отклонение случайной величины, S_кр – среднеквадратическое отклонение, вычисляемое как корень квадратный из дисперсии продолжительности критического пути. Соответствие между Z и Ф(Z) представлено в таблице.
Таблица — Таблица стандартного нормального распределения.

Z	F(Z)	Z	F(Z)	Z	F(Z)
0	0.0000	1.0	0.6827	2.0	0.9643
0.1	0.0797	1.1	0.7287	2.1	0.9722
0.2	0.1585	1.2	0.7699	2.2	0.9786
0.3	0.2358	1.3	0.8064	2.3	0.9836
0.4	0.3108	1.4	0.8385	2.4	0.9876
0.5	0.3829	1.5	0.8664	2.5	0.9907
0.6	0.4515	1.6	0.8904	2.6	0.9931
0.7	0.5161	1.7	0.9104	2.7	0.9949
0.8	0.5763	1.8	0.9281	2.8	0.9963
0.9	0.6319	1.9	0.9545	2.9	0.9973

Критический путь проходит по работам (1,2)(2,3)(3,6)(3,8).
Дисперсия критического пути:
S 2 ­(L_кр)= S 2 (1,2)+ S 2 (2,3)+ S 2 (3,6)+S 2 (6,8)=1+0,25+4+1=6,25
S(L_кр)=2,5
p(t_кр<30)=0,5+0,5Ф((30-32)/2,5)=0,5-0,5Ф(0,8) = 0,5-0,5*0,5763=0,5-0,28815=0,213
Вероятность того, что весь комплекс работ будет выполнен не более чем за 30 дней, составляет 21,3%.
Для определения максимально возможного срока выполнения всего комплекса работ с надежностью 95% будем использовать следующую формулу: T=Т_кр+Z*S_кр Для решения поставленной задачи найдем значение аргумента Z, которое соответствует заданной вероятности 95% (значению графы Ф(Z) 0,9545*100% в таблице 5 соответствует Z=1,9).
T=32+1,9*2,5=36,8
Максимальный срок выполнения всего комплекса работ при заданном уровне вероятности 95% составляет всего 36,8 дня.

Источник

1.3.5. Пример построения и расчета сетевой модели

Исходные данные варианта лабораторной работы включают название и продолжительность каждой работы (табл. 1.1), а также описание упорядочения работ.

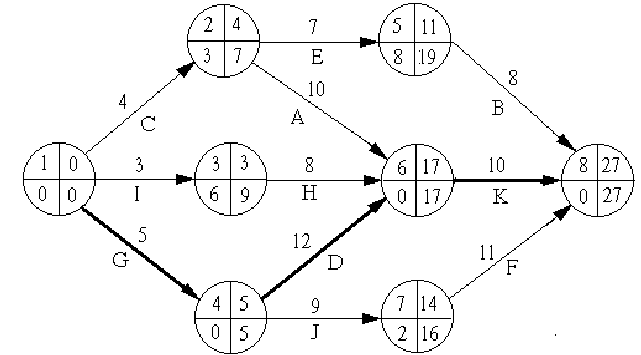
1. Работы C, I, Gявляются исходными работами проекта, которые могут выполняться одновременно.
2. Работы E иAследуют за работойC.
3. Работа Hследует за работойI.
4. Работы D иJследуют за работойG.
5. Работа Bследует за работойE.
6. Работа Kследует за работамиAиD, но не может начаться прежде, чем не завершится работаH.
7. Работа Fследует за работойJ.

На рис.1.4 представлена сетевая модель, соответствующая данному упорядочению работ. Каждому событию присвоен номер, что позволяет в дальнейшем использовать не названия работ, а их коды (см. табл. 1.2). Численные значения временных параметров событий сети вписаны в соответствующие секторы вершин сетевого графика, а временные параметры работ сети представлены в табл. 1.3. Таблица 1.2 Описание сетевой модели с помощью кодирования работ

Номера событий		Код работы	Продолжительность
начального	конечного	работы
1	2	(1,2)	4
1	3	(1,3)	3
1	4	(1,4)	5
2	5	(2,5)	7
2	6	(2,6)	10
3	6	(3,6)	8
4	6	(4,6)	12
4	7	(4,7)	9
5	8	(5,8)	8
6	8	(6,8)	10
7	8	(7,8)	11

Рис.1.4. Сетевая модель Таблица 1.3 Временные параметры работ

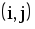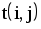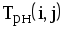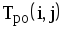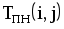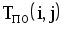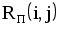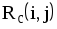1,2	4	0	4	3	7	3	0
1,3	3	0	3	6	9	6	0
1,4	5	0	5	0	5	0	0
2,5	7	4	11	12	19	8	0
2,6	10	4	14	7	17	3	3
3,6	8	3	11	9	17	6	6
4,6	12	5	17	5	17	0	0
4,7	9	5	14	7	16	2	0
5,8	8	11	19	19	27	8	8
6,8	10	17	27	17	27	0	0
7,8	11	14	25	16	27	2	2

1.4. Контрольные вопросы

1.4.1. Зачетный минимум

1. Определение события, виды событий, практические примеры событий, обозначение событий на графике, временные параметры событий.
2. Определение работы, классификация работ с приведением соответствующих практических примеров, обозначение работ на графике, временные параметры работ.
3. Правила построения сетевых графиков.
4. Определение пути в сетевом графике, виды путей, важность определения критического пути.
5. Умение вычислять временные параметры событий и работ.

1.4.2. Дополнительные вопросы

1. Почему при расчете раннего срока свершения события iвыбираютмаксимальнуюиз сумм ?
2. Почему при расчете позднего срока свершения события iвыбираютминимальнуюиз разностей ?
3. Какова взаимосвязь полного и свободного резервов работы?
4. Как можно найти критических путь в сетевой модели, без непосредственного суммирования длительностей работ?

Часть 2. ОПТИМИЗАЦИЯ СЕТЕВЫХ МОДЕЛЕЙ ПО КРИТЕРИЮ «МИНИМУМ ИСПОЛНИТЕЛЕЙ» 2.1. ЦЕЛЬ РАБОТЫ Знакомство с методикой и приобретение навыков проведения оптимизации сетевых моделей по критерию «Минимум исполнителей». 2.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Согласно номеру своего варианта получите данные о количество исполнителей, занятых на каждой работе сетевой модели, и ограничение по численности Nодновременно занятых в работе исполнителей. 2. Постройте в отчете графики привязки и загрузки, используя нормальные длительности работ сети — 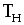(см. п.2.3.1), и покажите их преподавателю. 3. Проверьте правильность построения графиков привязки и загрузки с помощью компьютера, в случае необходимости выявите и устраните ошибки. 4. Используя компьютерную программу, проведите уменьшение численности исполнителей, одновременно занятых на работах сети, до требуемого уровня N. 5. Отчет по лабораторной работе должен содержать:

• номер варианта;
• исходные данные варианта;
• графики привязки и загрузки до проведения оптимизации загрузки;
• графики привязки и загрузки после проведения оптимизации загрузки (возможно использование пунктирных линий на первоначально построенных графиках для отображение изменений в привязке работ и загрузке сети, вызванных сдвигами работ);
• коды работ, сдвинутых в процессе оптимизации, и время их сдвига.

Источник

Сетевое планирование

Основное назначение методологии сетевого планирования в управлении сократить до минимума продолжительность проекта. С помощью сетевых моделей руководитель может системно оценивать текущий и перспективный ход запланированных операций, за счет чего возможно управление процессом реализации проекта в целом. Календарно-сетевое планирование позволяет также рационально оперировать имеющимися в распоряжении ресурсами.

Основная цель сетевого планирования следует из его назначения: построить модель реализации проекта на основе формирования комплекса работ, задания их очередности, определить необходимые ресурсы и задачи, которые должны быть решены для завершения проекта. В итоге необходимо добиться сокращения до минимума продолжительности проекта.

Метод сетевого планирования позволяет координировать деятельность участников проекта, определить порядок, согласно которому должны выполняться запланированные работы, операции, действия. При этом основу составляет продолжительность каждой операции, действия, которые должны быть определены с учетом потребностей в материальных, трудовых и финансовых ресурсах.

Сетевое планирование – это метод управления, основанный на математическом аппарате теории графов и системного подхода, преследует задачи объективного построения плана операций на заданный период времени за счет алгоритмизации взаимосвязанных работ. Благодаря такому подходу достигается поставленная цель.

Применение методологии сетевого планирования в управлении предполагает формализацию структуры операций в информационно-табличном виде, на основе чего осуществляется структуризация операций по отрезкам времени и группировка параллельных операций для оптимального выполнения всего проекта в целом. На основе этого осуществляется построение таблицы операций, в которую сводятся все значимые данные по каждой операции в соответствии с формализованной структурой операций и группами параллельных операций. Результатом является построение сетевой диаграммы, которая подлежит корректировке в случае несоответствия запланированных действий общему сроку их выполнения, либо отдельным промежуткам времени внутри общей временной структуры проекта.

Задачи сетевого планирования:

1. Определить перечень критических работ или операций (т.е. таких операций, которые имеют наибольшее влияние на общую продолжительность проекта);
2. Построить сетевой план проекта таким образом, чтобы все запланированные работы и операции были произведены с соблюдением заданных сроков и минимальных затратах.

Единица такой сетевой модели – операция (работа или задача), которая означает какую-либо деятельность, в результате выполнения которой будут достигнуты определенные результаты.

Результатом сетевого планирования является графическое отображение последовательности операций, выполнение которых приведет к достижению конечной цели проекта. Основным способом отображения являются сетевые экономико-математические модели. Для управленческой деятельности наиболее подходят сетевые графики. С помощью сетевой модели формируется возможность системного представления всех операций и условия для управления процессом осуществления проекта. При необходимости метод сетевого планирования позволяет маневрировать ресурсами в рамках модели для достижения конечной цели.

Часто руководители склонны опираться лишь на личный опыт, который ограничен и субъективен. Такой ограниченный уровень компетентности редко помогает в динамичном окружении, а иногда может принести прямой вред.

Сетевое планирование позволяет исключить влияние субъективных факторов на управление проектом, способствуя сокращению сроков реализации проекта минимум на 15-20%, рационализации использования имеющихся ресурсов и оптимизации затрат. При этом отдельные операции рассматриваются как отдельные элементы целостной системы, а исполнители выступают звеньями данной системы.

Методы сетевого планирования

Применяя сетевые диаграммы (граф сети, PERT-диаграммы), следует учитывать следующие аспекты:

• сетевая диаграмма отражает полный комплекс работ и этапов проекта;
• на сетевом графике должны быть установлены зависимости между операциями;
• сетевые графики не являются блок-схемами;
• сетевые диаграммы содержат только операции и логические зависимости между ними (отсутствуют входы, процессы, выходы и т.д.);
• сетевые модели не допускают повторяющихся циклов, этапов, «петель» операций.

Сетевое планирование ориентировано на сокращение до минимума продолжительности проекта, для жтого могут применяться два метода:

«Максимальный по продолжительности полный путь в сети называется критическим; работы, лежащие на этом пути, также называются критическими. Именно длительность критического пути определяет наименьшую общую продолжительность работ по проекту в целом» [1]. Увеличение или сокращение времени выполнения операций критического пути ведет к росту и снижению продолжительности проекта соответственно. Метод критического пути предполагает расчет графиков работ, продолжительности каждой работы, чтобы определить критический путь проекта, а затем принять меры по его сокращению.

Метод оценки и пересмотра планов заключается в соблюдении графиков проектирования, производства, организации работ и других установленных сроков. Согласно этой методике, весь проект «разбивается» на ряд подзадач, и для каждой задачи оценивается время, необходимое для ее выполнения, каждой задаче также назначается приоритет выполнения. В зависимости от приоритета задачи и ее влияния на проект предпринимаются меры по оптимизации ее выполнения для снижения продолжительности проекта.

Таким образом, процесс сетевого планирования заключается в описании конкретного проекта или плана действий на заданный период в виде определенного комплекса мероприятий, задач, мер, процедур или работ.

При этом соблюдается объектная взаимосвязь между всеми процедурами и операциями, которые включены в структуру проекта или плана действий на заданный период. Развитие методик управления проектами в начале XXI века привело к тому, что в случае несоответствия реальной технологии выполнения работ сетевое планирование превращается в «формальную галочку», как следствие, дискредитируется сама идея использования технологий календарно-сетевого планирования.

Методика построения сетевых моделей

Сетевые диаграммы отображают сетевую модель конкретного проекта или плана действий на заданный период в виде множества вершин, которые соответствуют запланированным в рамках данного плана операциям и процедурам. Каждая вершина соединена с предшествующей и следующей вершинами логическими линиями, представляющими взаимосвязь между операциями. Исключение составляют начальная и финальная вершина, соответствующие первой и последней операции в рамках конкретного проекта или плана действий в заданном периоде.

Перед непосредственным построением сетевой диаграммы проводится работа по формированию операций в рамках конкретного проекта или плана действий на заданный период. Предварительно составляется формализованная структура операций в табличной форме.

Пример формализованной структуры операций

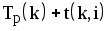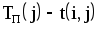Источник