4.Сетевой график и его назначение. Полный путь. Критический путь.
Сетевой график — это графическая модель некоторого комплекса взаимосвязанных работ (проекта или производственного процесса).
Дугам графа соответствуют работы, т.е. отдельные операции проекта (дуга на графике изображается стрелкой). Работа имеет продолжительность и может требовать ресурсов. Над дугой может быть указана числовая характеристика работы (например, время ее выполнения).
Вершинам графа соответствуют события (вершина изображается кружком или квадратиком). Событие означает факт окончания всех работ, в него входящих, и начала всех работ, из него исходящих. Пока не выполнены все работы, входящие в событие, не может свершиться само событие и, следовательно, не может быть начата ни одна из работ, выходящих из него. Событие не имеет продолжительности и не требует ресурсов.
Полный путь – это цепочка следующих друг за другом работ, соединяющих исходное и завершающее событие. В примере можно выделить следующие полные пути (они обозначаются номерами событий, через которые проходят):
Критическим называется полный путь, имеющий наибольшую продолжительность во времени. Критических путей на сетевом графике может быть несколько (при этом все они имеют одинаковую продолжительность).
Продолжительность критического пути определяет критический срок проекта tкр. Все остальные (некритические) полные пути выполняются параллельно с критическим путем (цепочкой работ) и завершаются раньше. Критический срок, таким образом, показывает, за какое минимальное время может быть завершен весь проект. Очевидно, что увеличение сроков выполнения проекта больше tкр невыгодно.
Работы, принадлежащие критическому пути, называются критическими. Они не имеют резервов времени. Их несвоевременное выполнение ведет к срыву сроков всего проекта.
В нашем примере определить критический путь легко: нужно перебрать все возможные полные пути, рассчитать продолжительность каждого из них и выбрать наибольший:
Критическим является полный путь μ2, т.к. он имеет наибольшую продолжительность. Критический путь принято выделять на графике жирной линией (рис.2.3.).
Однако, если сетевой график достаточно сложный, перебрать все возможные пути затруднительно. Поэтому используют более формальный подход:
Для каждого события рассчитывают ранний и поздний сроки свершения.
На их основе определяют резервы времени всех событий и работ.
Проводят критический путь по тем работам и событиям, которые не имеют резерва времени.
5 Параметры событий сетевого графика. Параметры работ.
Ранний срок свершения события – это самый ранний момент, к которому завершаются все работы, предшествующие этому событию.
Ранний срок свершения события рассчитывается последовательно для каждого события от исходного к завершающему по следующим формулам:
, т.е. начало проекта принимается за нулевой момент времени;
, если событию j предшествует только одна работа;
, если событию предшествует несколько работ.
Здесь ij – множество работ, заканчивающихся j-м событием (дуги, входящие в вершину j);
–ранний срок свершения события, с которого начинается работа (i,j);
–продолжительность работы (i,j).
Резерв времени события показывает, на какой предельно допустимый срок может задержаться свершение события без нарушения критического срока проекта:
Полный резерв времени работы показывает, на сколько можно увеличить время выполнения этой работы при условии, что срок выполнения всего комплекса работ не изменится.
Резервы работ определяются на основе параметров свершения событий по следующей формуле:
Критические работы резервов времени не имеют, т.е. еще раз убеждаемся в том, что критический путь мы выделили правильно.
Резервы времени работ рассчитываются для организации контроля над выполнением проекта. Кроме того, зная эти резервы, можно оптимизировать срок выполнения проекта. Например, можно забрать ресурсы у тех работ, которые имеют резерв времени (снять часть рабочих с этих работ или урезать их финансирование) и передать их работам, лежащим на критическом пути. Тогда критические работы смогут быть выполнены раньше, что повлечет уменьшение критического срока всего проекта. Поскольку при таком перераспределении ресурсов критический путь может измениться, задача оптимизации критического срока является многоэтапной и может быть решена с использованием компьютера.
Этап 3. Расчет параметров сетевой модели графическим методом; определение критического пути и его продолжительности.
- Ранний срок свершения события
;
- Поздний срок свершения события
;
- Резерв времени события
;
- Полный резерв времени события
;
- Свободный резерв времени события
.
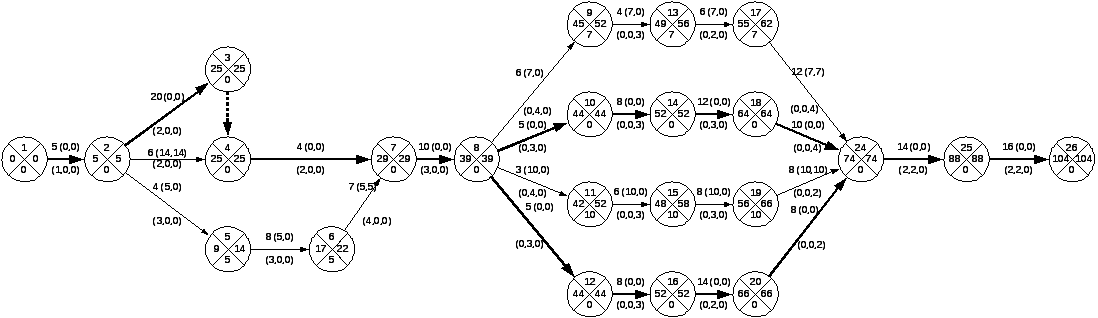
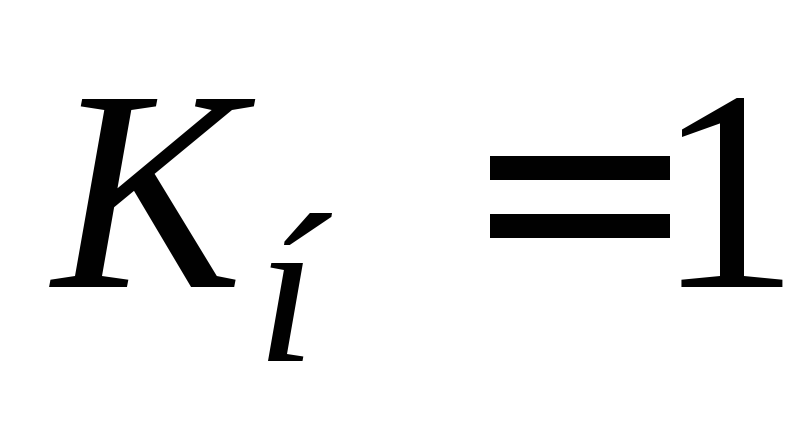
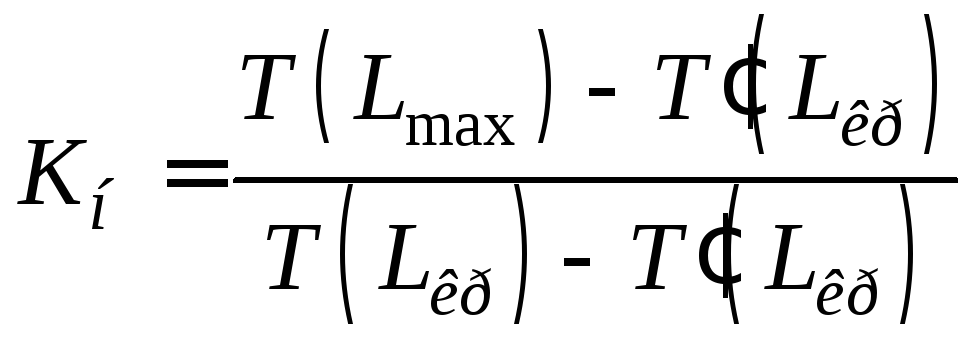
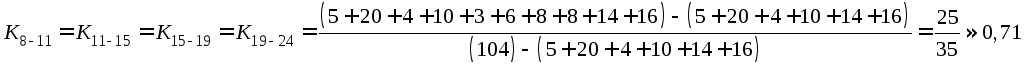
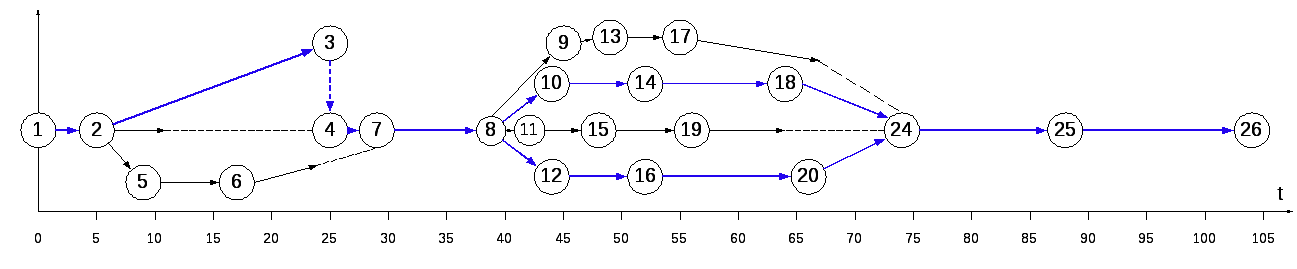
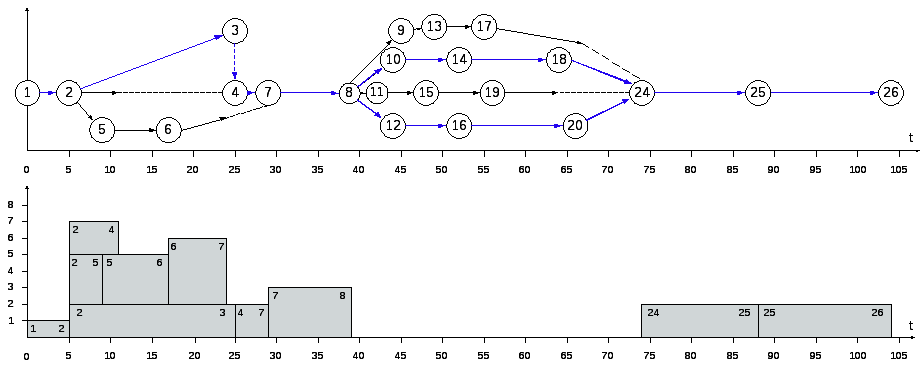
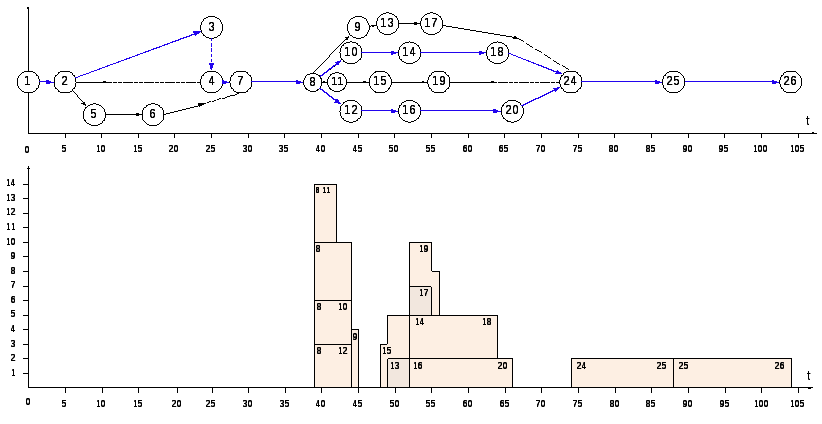
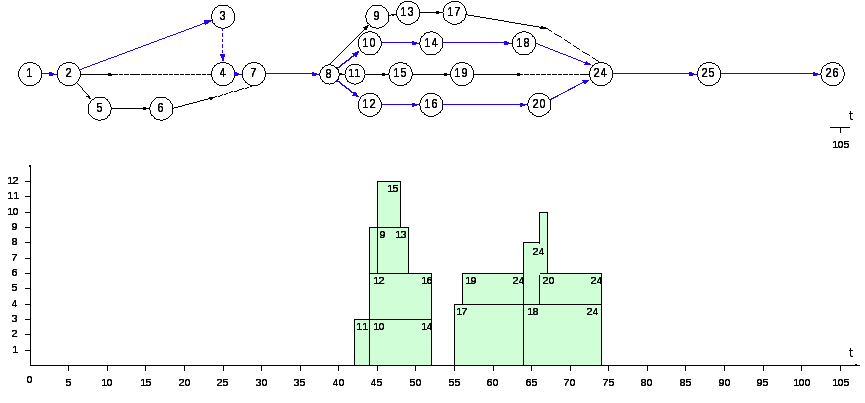
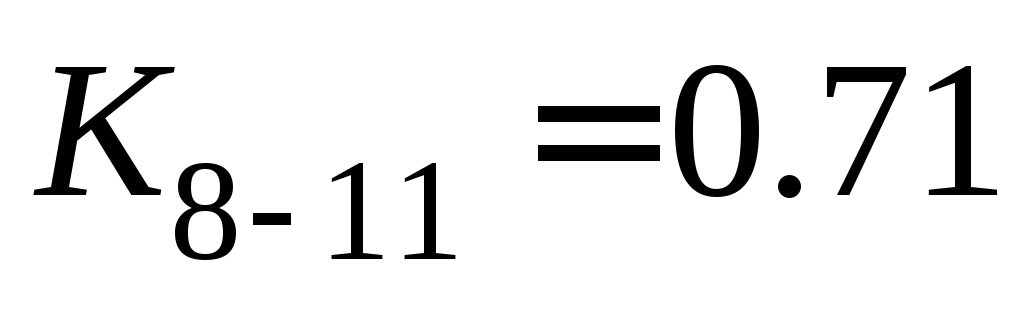
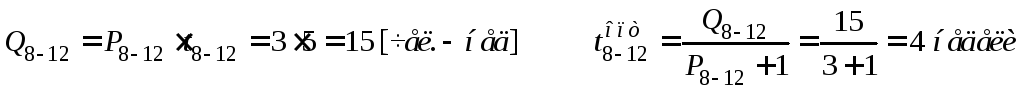
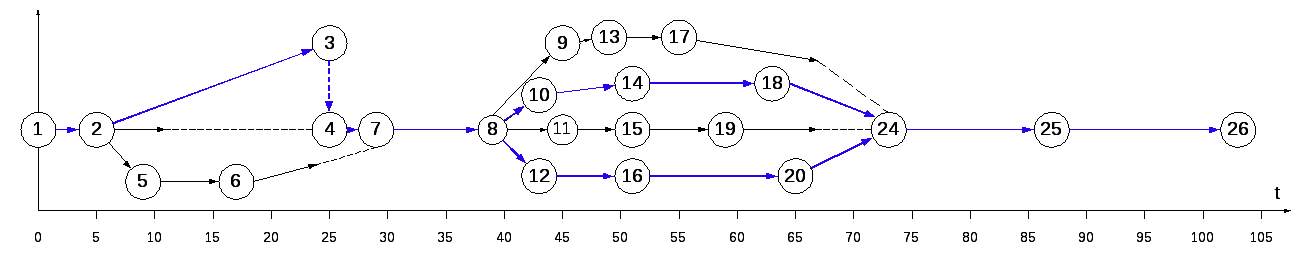
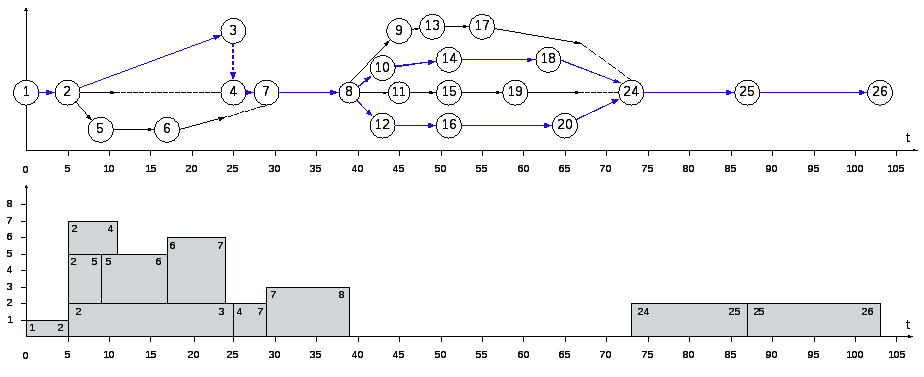
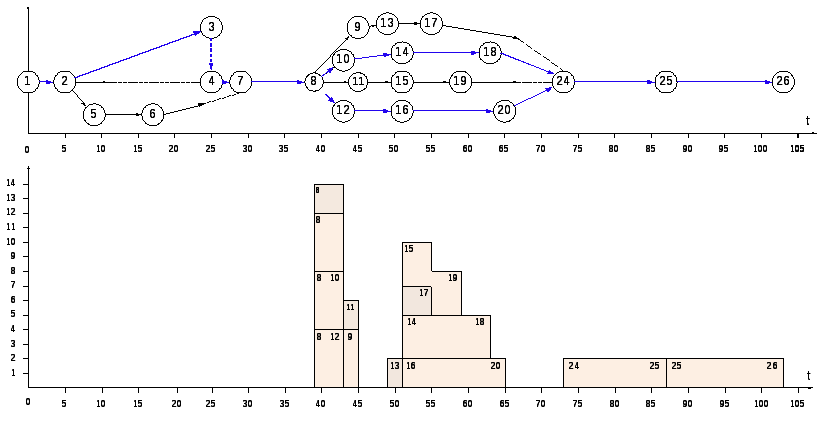
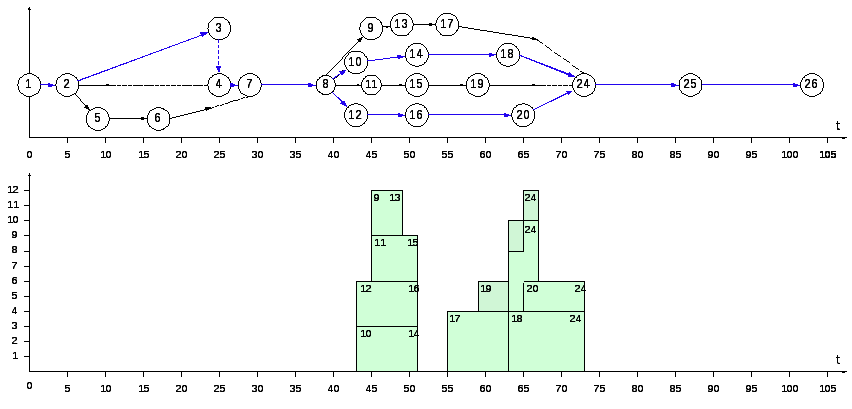
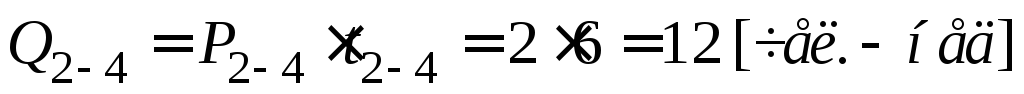
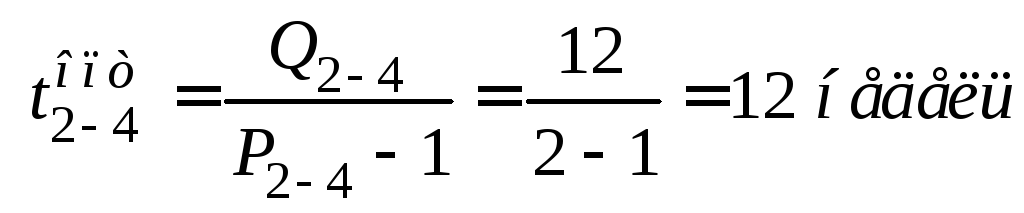
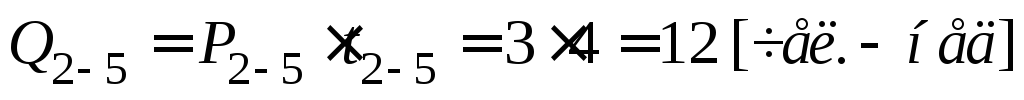
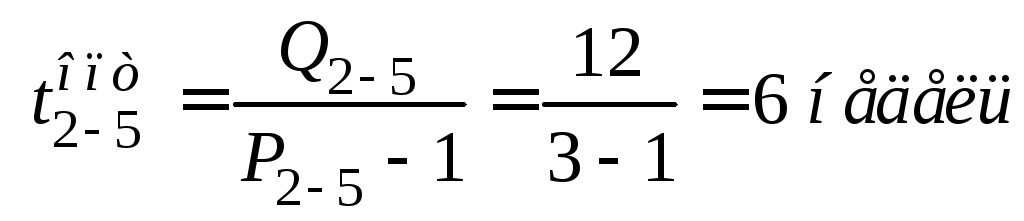
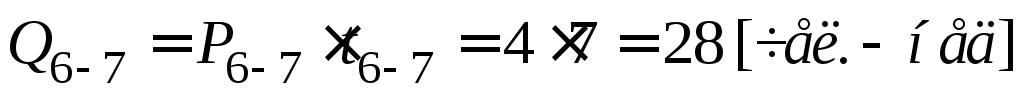
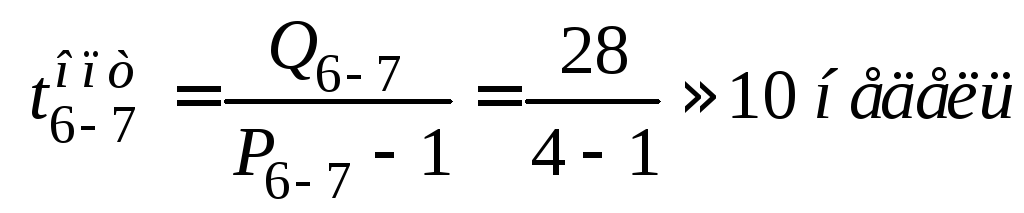
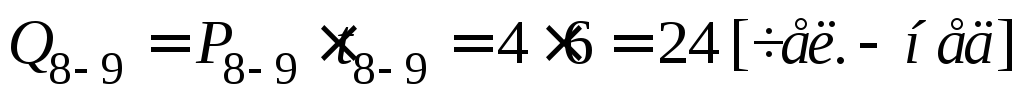
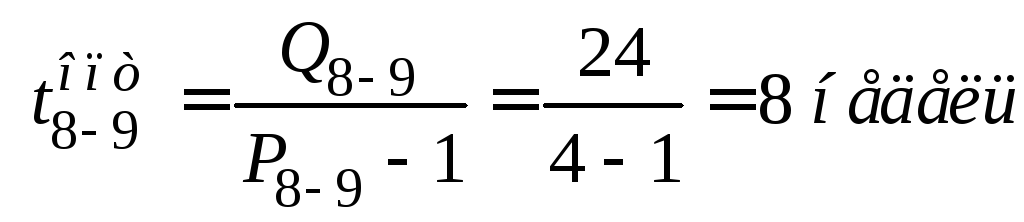
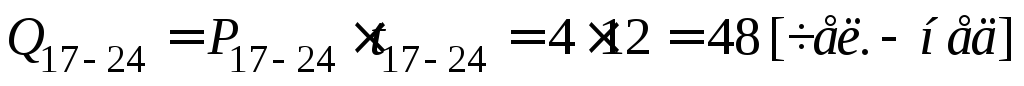
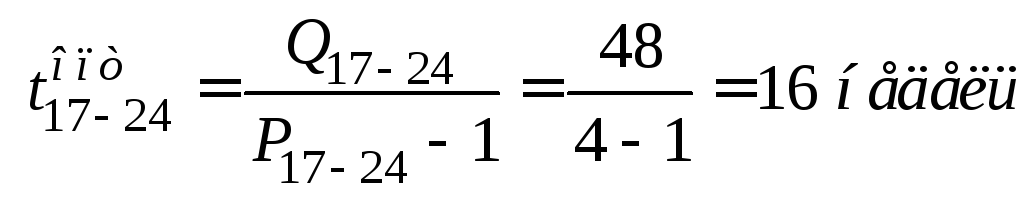
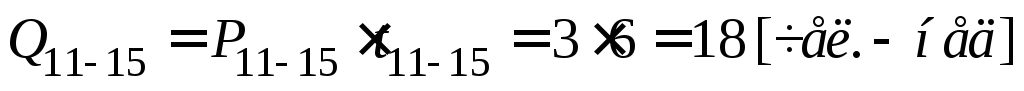
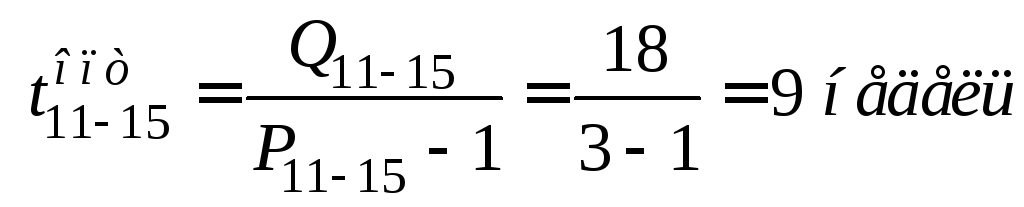
Определение критического пути
Будем предполагать, что время выполнения каждой работы точно известно. Введем следующие определения.
Путь— последовательность взаимосвязанных работ, ведущая из одной вершины проекта в другую вершину. Например (см. Рисунок 48), и – два различных пути.
Рисунок 48. Различные пути на сетевом графике
Длина пути— суммарная продолжительность выполнения всех работ пути.
Полный путь— это путь от исходного к завершающему событию.
Критический путь— полный путь, суммарная продолжительность выполнения всех работ которого является наибольшей.
Очевидно, что минимальное время, необходимое для выполнения любого проекта равно длине критического пути. Именно на работы, принадлежащие критическому пути, следует обращать особое внимание. Если такая работа будет отложена на некоторое время, то время окончания проекта будет отложено на то же время. Если необходимо сократить время выполнения проекта, то в первую очередь нужно сократить время выполнения хотя бы одной работы на критическом пути.
Для того, чтобы найти критический путь, достаточно перебрать все пути и выбрать тот, или те из них, которые имеют наибольшую суммарную продолжительность выполнения работ. Однако для больших проектов реализация такого подхода связана с вычислительными трудностями. Метод критического пути (метод CPM — Critical Path Method) позволяет получить критический путь намного проще.
Расчет сетевой модели начинают с временных параметров событий, которые вписывают непосредственно в вершины сетевого графика (Рисунок 49):
–ранний срок наступления события i, минимально необходимый для выполнения всех работ, которые предшествуют событию i;
–поздний срок наступления события i, превышение которого вызовет аналогичную задержку наступления завершающего события сети;
–резерв события i, т.е. время, на которое может быть отсрочено наступление события i без нарушения сроков завершения.

- для исходного события S:
;
- для всех остальных событий i:
,
где максимум берется по всем работам (k,i), входящим в событие i; 


- для завершающего события F:
;
- для всех остальных событий i:
,
где минимум берется по всем работам (i,j), выходящим из события i; 

- необходимое условие: нулевые резервы событий, лежащих на критическом пути
;
- достаточное условие: нулевые полные резервы работ, лежащих на критическом пути
.
— показывает максимальное время, на которое можно увеличить длительность работы (i,j) или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом.
Пример Рассмотрим пример. Компания разрабатывает строительный проект. Исходные данные по основным операциям проекта представлены в таблице. Нужно построить сетевую модель проекта, определить критические пути и проанализировать, как влияет на ход выполнения проекта задержка работы D на 4 недели.
| Работа | Непосредственно предшествующая работа | Длительность, недели |
| A | — | 4 |
| B | — | 6 |
| C | A, B | 7 |
| D | B | 3 |
| E | C | 4 |
| F | D | 5 |
| G | E,F | 3 |
Сетевой график проекта показан на рисунке ниже (см. Рисунок 52). 
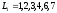


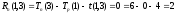










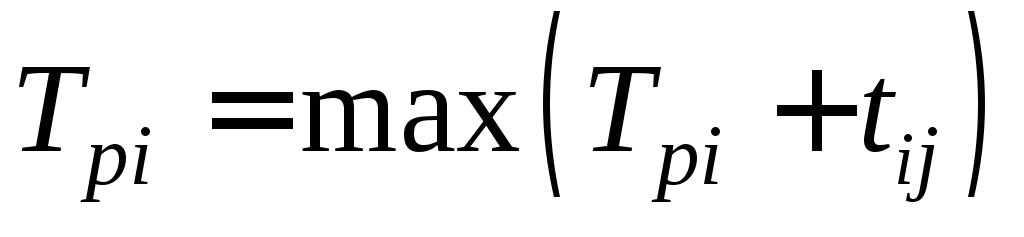 ;
;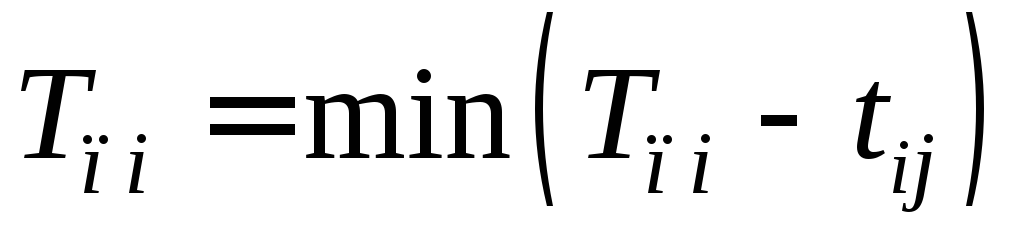 ;
;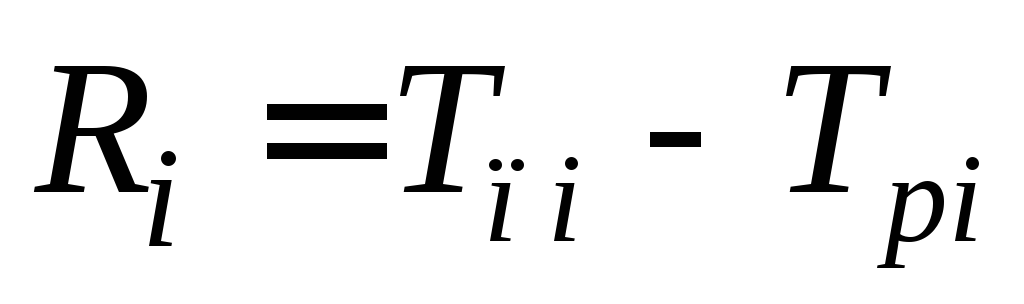 ;
;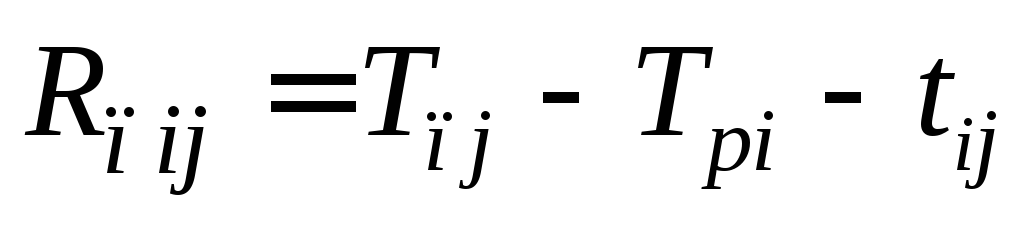 ;
;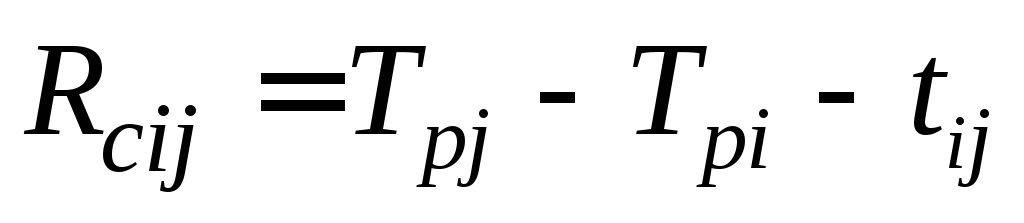 .
.


 –ранний срок наступления события i, минимально необходимый для выполнения всех работ, которые предшествуют событию i;
–ранний срок наступления события i, минимально необходимый для выполнения всех работ, которые предшествуют событию i; –поздний срок наступления события i, превышение которого вызовет аналогичную задержку наступления завершающего события сети;
–поздний срок наступления события i, превышение которого вызовет аналогичную задержку наступления завершающего события сети; –резерв события i, т.е. время, на которое может быть отсрочено наступление события i без нарушения сроков завершения.
–резерв события i, т.е. время, на которое может быть отсрочено наступление события i без нарушения сроков завершения. ;
; ,
, ;
; ,
, ;
; .
. — показывает максимальное время, на которое можно увеличить длительность работы (i,j) или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом.
— показывает максимальное время, на которое можно увеличить длительность работы (i,j) или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом.