Практическое занятие №2 Параметры сетевой модели
1. Установление полного перечня работ, которые необходимо выполнить при планировании комплекса работ.
2. Составление топологии сети — четкой последовательности и взаимосвязей всех работ и построение сетевого графика.
3. Оценка продолжительности выполнения отдельных работ.
4. Расчет параметров сетевого графика.
5. Анализ и оптимизация сетевого графика.
6. Управление ходом работ по сетевому графику.
2. Параметры сетевой модели
В системах СПУ применяются различные типы сетевых моделей, отличающиеся составом информации о комплексе работ.
Встречаются модели с детерминированной и вероятностной структурой сети, с детерминированными и вероятностными оценками продолжительности работ сети. При выборе модели руководителю проекта приходится принимать компромиссное решение: с одной стороны, сетевая модель должна быть простой, а с другой – адекватной объекту.
Широкое применение получила сетевая модель ПДВ (простейшая детерминированная временная), которая характеризуется следующими тремя моментами:
а) имеется сеть с единственным исходным и единственным завершающим событием;
б) продолжительности всех работ tijизвестны, однозначно определены (вспомните из математики: детерминант – определитель) и указаны на графике (обычно в днях, в зарубежной практике – чаще в неделях);
в) задан момент начала выполнения комплекса Т0,а также задается (но не обязательно) директивный срокТдир наступления завершающего события.
Рассмотрим временные параметры этой модели.
По известным продолжительностям работ легко определить продолжительность каждого пути – t(L).Продолжительность любого пути равна сумме продолжительностей работ, его составляющих:
(1)
Для пояснения обратимся к рис.1. На графике над стрелками указаны продолжительности работ в днях (напомним, что продолжительность фиктивной работы равна нулю).
Найдем на графике полные пути и определим их продолжительность (по номерам событий):
L1 1 – 2 – 5 – 7 – 8 t(L1) = 14 дн.
L2 1 – 2 – 4 – 5 – 7 – 8 t(L2) = 12 дн.
L3 1 – 3 – 4 – 5 – 7 – 8 t(L3) = 13 дн.
L4 1 – 3 – 6 – 7 – 8 t(L4) = 16 дн.
Всегда найдется путь, имеющий наибольшую продолжительность, он называется критическим–Lкр. Его продолжительность получила особое обозначение:
t(Lкр)=Ткр .
Понятие критического пути является центральным понятием в системе СПУ. Значение Lкр, во-первых, состоит в том, что он является самым длинным путем в сети и, таким образом, является единственным путем, который определяет полную продолжительность процесса. Поэтому, если мы хотимопределитьполную продолжительность процесса, нужно определитьТкр, а определять для этой цели все остальныеt(L) не имеет смысла. Во-вторых, если мы хотимсократитьпродолжительность процесса, нужно прежде всего сокращать продолжительность работ, принадлежащихLкр. Таким образом, логика сетевого планирования приводит нас к необходимости находить в сетях критические пути и определять их продолжительность.
На графике рис. 1 путь L4имеет наибольшую продолжительность, равную 16 дням, и потому является критическим. Обычно критический путь на графиках выделяется (цветными, двойными, жирными и т.п. стрелками).
Обратим внимание, что в сети может быть несколько критических путей (с точки зрения использования ресурсов – чем больше критических путей в графике, тем лучше).
Обычно к Lкр принадлежит 10-15 % работ. Чем сложнее сеть, тем таких работ меньше (считается, что в сети средней сложности количество работ в 1,7 раза превышает количество событий).
Другие полные пути рассматриваемого сетевого графика могут либо полностью проходить вне критического пути (L1иL2), либо частично с ним совпадать (L3). Эти пути называютсяненапряженными: на участках, не совпадающих с критической последовательностью работ, они имеют резервы времени. Задержка в наступлении событий, лежащих на этих участках, до определенного момента не влияет на срок завершения всего комплекса.
Из ненапряженных путей наибольшее внимание привлекают наименее напряженные и подкритические. Подкритические путиимеют продолжительность, близкую кТкр(отличаются отТкрна определенную величину, устанавливаемую руководителем проекта). Эти пути могут стать критическими в результате задержки выполнения их работ или в результате сокращения продолжительности работ, лежащих на критическом пути, и, следовательно, являются потенциально опасными с точки зрения соблюдения сроков завершения проекта.
Например, при увеличении времени выполнения работы 2-5 (рис. 1) на 2 дня это приведет к тому, что t(L1) = 16 дн. =Ткр. ТогдаL1тоже станет критическим и будет определять срок выполнения всего комплекса.
Наименее напряженные пути могут рассматриваться с точки зрения возможности использования ресурсов (рабочей силы, оборудования, денежных средств). Возможное удлинение этих путей, вызванное переброской ресурсов, до определенных пределов не опасно для сроков проекта.
Работы, принадлежащие критическому и подкритическим путям, составляют критическую зонукомплекса (15-20 % всех работ).
Зная продолжительность всех работ, можно также определить сроки наступления всех событий сети. Для каждого события определяют ранний и поздний сроки его наступления.
Ранний срок наступления события– это минимальный из возможных моментов его наступления, когда будут выполнены все работы, предшествующие данному событию. Он определяется максимальной из продолжительностей всех путей, предшествующих данному событию:
(2)
где — путь, предшествующий данному событиюi;
— максимальный из этих путей.
Поясним это на примере рис. 1. Событию 5 предшествуют три пути: 1-2-5 с продолжительностью 7 дн., 1-2-4-5 с продолжительностью 5 дн. и 1-3-4-5 с продолжительностью 6 дн. Событие 5 не может наступить ранее 7 дней, т.к. только в течение этого периода будут выполнены все предшествующие ему работы 2-4, 3-4 и 2-5.
Легко увидеть, что для события 3 ранний срок его наступления = 4 дн., т.к. ему предшествует только один путь 1-2, состоящий из одной работы.
Поздний срок наступления события— это максимальный из допустимых моментов его наступления, при котором еще не изменяется общий срок выполнения всего комплекса. Поздний срок определяется разностью междуТкри наибольшей из продолжительностей путей, следующих за событиемi:
(3)
где — путь, следующий за событиемi;
— максимальный из этих путей.
Продолжим рассмотрение рис. 1. За событием 5 следует только один путь 5-7-8 продолжительностью 7 дней. Следовательно,
= 16 – 7 = 9 дн.
За событием 3 следуют два пути: 3-4-5-7-8 с продолжительностью 9 дн. и 3-6-7-8 с продолжительностью 12 дн. Следовательно, = 16 – 12 = 4 дн., т.е. событие 3 не может наступить позже 4 дней от начала работ, иначе это скажется на изменении срока всего комплекса.
Так как по определению критического пути
, (4)
то для всех событий, принадлежащих критическому пути, справедливо равенство:
(5)
В справедливости этого мы уже убедились из рассмотренного примера для события 3. Оно лежит на критическом пути, поэтому


Зная сроки наступления событий, можно для каждой работы сети определить сроки ее начала и окончания, выявив тем самым возможности смещения сроков. Применительно к каждой работе рассматриваются четыре срока:
- ранний срок начала работы
; (6)
- ранний срок окончания работы
; (7)
- поздний срок начала работы
; (8)
- поздний срок окончания работы
. (9)
С учетом равенства (5) для событий, лежащих на критическом пути, можно сделать вывод, что у работ критического пути ранние и поздние сроки начала или окончания совпадают: 


















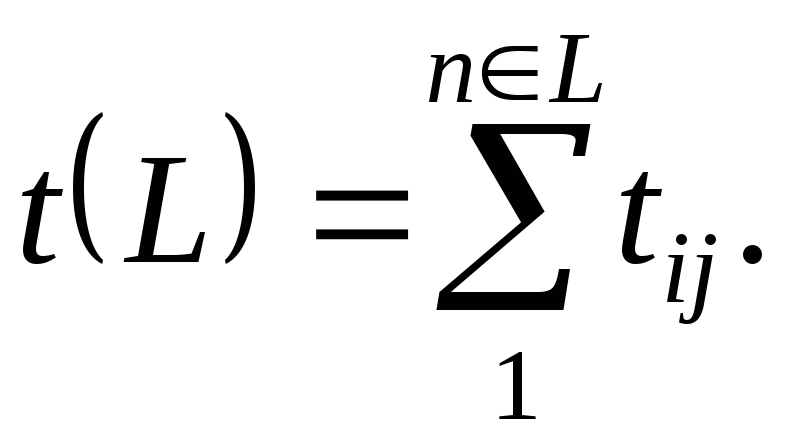

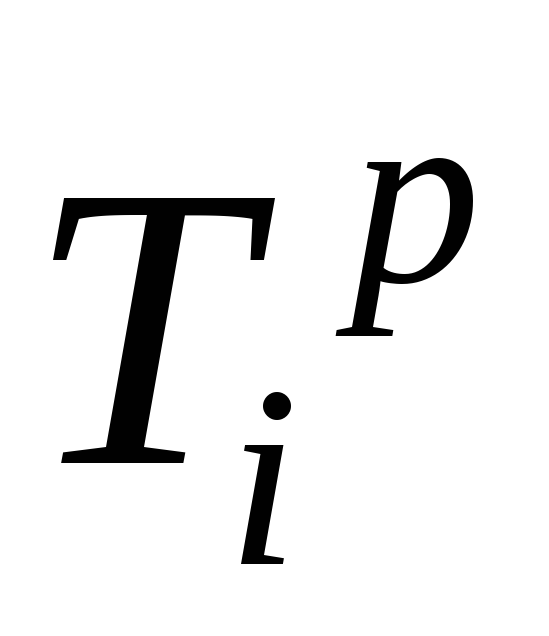




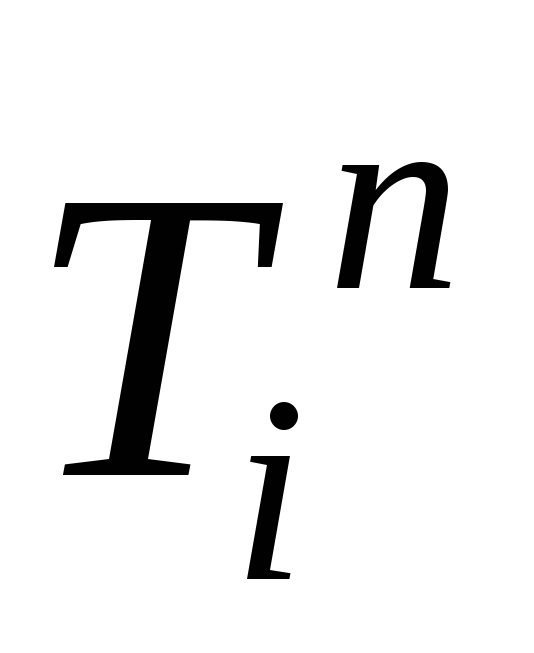







 ; (6)
; (6) ; (7)
; (7) ; (8)
; (8) . (9)
. (9)