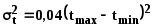Продолжительность выполнения работ сетевой модели

3. Определение продолжительности работ

Одним из наиболее важных этапов составления сетевой модели является получение правильных оценок продолжительности работ. Продолжительности работ могут быть определены либо по имеющим­ся нормативам, либо с использованием экспертных вероятностных оценок.

Формулы для определения ожидаемой продолжительности ра­бот вторым методом в зависимости от количества экспертных оценок представлены в табл. 1.

Расчетные зависимости для установления ожидаемой продол­жительности выполнения работ и ее дисперсии на основе экспертных оценок

Наименование параметра

Ожидаемая продолжительность вы­полнения работы

на основе трех экспертных оценок

Ожидаемая продолжительность вы­полнения работы

на основе двух экспертных оценок

Дисперсия (мера разброса) ожидае­мой

продолжительности работы при трех оценках

Дисперсия (мера разброса) ожидае­мой

продолжительности работы при двух оценках

Условные обозначения к таблице:

t_min – минимальная продолжительность работы, выбранная из условия, что выполнение работы будет протекать при наиболее благоприятных обстоятельствах;

t_нв – наиболее вероятная продолжительность работы, выбранная при средних условиях, при которых не возникает никаких неожиданных трудностей;

t_max – максимальная продолжительность работы, выбранная из условия выполнения данной работы при самом неблагоприятном стечении об­стоятельств.

4. Расчет параметров сетевой модели

К основным параметрам сетевой модели относятся характери­стики событий, работ, резервы времени событий и работ. Эти пара­метры являются исходными для получения ряда дополнительных ха­рактеристик, а также для анализа сети или составления плана разра­ботки.

При небольших размерностях сетевой модели (до 100 событий) рассчитываются графическим методом параметры событий, а при больших — табличным методом параметры работ.

Порядок расчета параметров событий

Расчету подлежат следующие параметры:

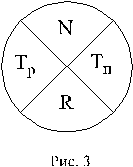
Т_р – наиболее ранний возможный срок свершения события;

Т_п – наиболее поздний допустимый срок свершения события;

R – резерв времени события.

Расчет выполняется непосредственно на модели. В этом случае событие изображается кружком диаметром 15- 20 мм, разделенным на четыре сектора (рис. 3). Буквой N обозначен номер события.

Расчет выполняется по следующим правилам:

Осуществляется проход сетевой модели от исходного собы­тия к завершающему и последовательно определяются ранние срокисвершения событий по формуле:

Т_pj = max (T_pi + t_ij) ,

где t_ij — ожидаемое время выполнения работы ij.

При этом ранний срок свершения исходного события принима­ется равным нулю: Т_ро = 0.

Поздний срок свершения завершающего события принимает­ся равным полученному значению его раннего срока свершения:

Этот срок определяет длину критического пути сетевой модели (Т_кр).

Осуществляется проход сетевой модели от завершающего со­бытия к исходному и последовательно определяются поздние срокисвершения событий по формуле:

T_пi = min (Т_пj — t_ij)

Необходимо обратить внимание на то, что полученное в резуль­тате расчета значение позднего срока свершения исходного события должно быть равно нулю:

T_пo = T_рo = 0

Рассчитываются резервы времени всех событий сетевой мо­дели по формуле:

R_i = T_пi — T_рi

Выделяется на сетевой модели (предпочтительно красным цветом) критический путь, как непрерывная последовательность работ от исходного события до завершающего с нулевыми резервами вре­мени событий.

Источник

1.5.Алгоритм определения оценок продолжительностей работ сетевой модели, обеспечивающих соблюдение директивных (желаемых) сроков

Сетевая модель отображает процесс во времени, соответствующий условиям исполнителя. Поэтому рассчитанный Ткр показывает общее время выполнения работ, которое может обеспечить данный исполнитель. Но, как правило, постановщиком задачи – заказчиком –является другая сторона. Заказчик имеет свои виды на срок выполнения работ. То есть, у заказчика есть свой Тдир, на который бы он хотел заключить контракт с исполнителем. Если Тдир ≥ Ткр, то исполнитель работ вынужден «доводить свой проект до желаемого Тдир. Этого можно достичь двумя путями:

• Изменять структуру (топологию) сетевой модели, доводя ее до срока Тдир. Но это сложный и длительный процесс.
• Изменять метрику (продолжительности работ) уже сформированной сетевой модели. Этот способ проще и рациональнее.

Воснове рекомендуемого изменения продолжительностей работ лежит следующая формула: t(ij) =t(ij) *K_н(ij) K_н(ij)= Tдир Ткр –R п (ij) , где (1.12) t(ij) – новая, измененная продолжительность работы; t(ij) – старая, заданная продолжительность работы (в соответствии с которой получено значение Ткр); Тдир – директивный желаемый срок выполнения всего комплекса работ; R п (ij) – полный резерв работы при первоначальном расчете. По формуле (1.12) производится пересчет всех продолжительностей работ. При этом некоторые работы будут уменьшаться по значению; другие увеличиваться; какие-то останутся без изменения. А именно: 1.Если ijЄLкр =>R п (ij) = 0, т.е. если работы принадлежат критическому пути, то К_н=Тдир/Ткр; и следовательно данные работы будут уменьшаться пропорционально величине Тдир/Ткр. 2 н(ij) < 1, то Тдир Ткр – R п (ij) Тдир < Ткр – R п (ij) R п (ij) < Ткр – Тдир (при условии Ткр >Тдир) Следовательно, все работы сетевой модели , у которых полный резерв меньшеразницы (Ткр – Тдир), будутуменьшеныпропорционально коэффициенту К_н(ij). 3.Если К_н(ij) > 1, тоR п (ij) > Ткр –Тдир. Следовательно, те работы, у которых полный резерв большеразницы (Ткр–Тдир), будут дажеувеличеныпропорционально К_н(ij) 4.Если К_н(ij) = 1, тоR п (ij) =Ткр – Тдир. Следовательно, если найдутся работы, у которых полный резерв равен разнице (Ткр – Тдир), то у них старая продолжительность не изменится. Рассмотренный алгоритм позволяет автоматически на основе расчета сетевой модели (табл.1.3), рассчитанного Ткр и заданного Тдир, получить измененные продолжительности работ; при этом можно утверждать, что если взять за основу измененные продолжительности работ, то проект будет выполнен за Тдир, т.е. Ткр изм =Тдир Рассмотрим пример, основываясь на сетевой модели (рис.1.11) и результатов расчета (табл.1.4). Пусть Тдир = 22 дня. То есть заказчика данного продукта не устраивает срок в 25 дней, который получился у исполнителя как Ткр = 25. В соответствии с выше приведенными рассуждениями можно сказать, что 1.Работы критического пути должны быть уменьшены пропорционально К_н(ij)= = Тдир22. Ткр 25 Это работы (1-5); (5-7); (7-6); (6-8) t(1-5) = 5*22/25 = 22/5 = 4,4 дня. и т.д. К_н(ij)= 2.Работы, у которыхR п (ij) < (25-22) = 3, должны быть также уменьшены, но пропорционально коэффициенту Тдир Ткр -R п (ij) В данной модели таких работ нет. 3.Работы, у которых R п (ij) > 3, могут быть увеличены. Это работы: (1-2); (1-4); (2-3); (3-6); (3-8); (7-8).

1. t(1-2) = 3* = 3* ≈3,7 22

25-7 18 и т.д. 4.Работы, у которых R п (ij) = 3, остаются без изменения. T(5-4) =8* = 8 22 25-3 Измененные таким образом продолжительности работ позволят обеспечить соблюдение Тдир срока создания проекта и удовлетворить желание заказчика.

Источник

Параметры сетевого графика и способы их расчета

Каждая работа сетевого графика имеет временную оценку — продолжительность tвыполнения работы. Для определения продолжительности и сроков выполнения каждой работы определяют следующие временные параметры сетевой модели: раннее начало работыt; раннее окончание работыt; позднее начало работыt;позднее окончание работыt;полный резерв времениR;свободный резерв времениr.Раннее начало работы— самый ранний момент начала работы. Раннее начало исходных работ сетевого графика равно нулю. Раннее начало любой работы равно максимальному раннему окончанию предшествующих работ.

Рис.7. Сетевой график строительства жилого дома с расчетом показателей:

а— в табличной форме;б —непосредственно на графике;в— форма записи расчетаРаннее окончание работы— самый ранний момент окончания данной работы, равный сумме раннего начала и продолжительности работы.Позднее начало работы— самый поздний момент начала работы, при котором продолжительность критического пути не изменяется. Он равен разности между поздним окончанием данной работы и ее продолжительностью.Позднее окончание работы— самый поздний момент окончания работы, при котором продолжительность критического пути не изменяется. У работ критического пути ранние и поздние сроки начала и окончания равны между собой, поэтому не имеют резервов времени. Работы, не лежащие на критическом пути, имеют резервы времени.Полный резерв времени— максимальное время, на которое можно увеличить продолжительность работы или перенести ее начало без увеличения продолжительности критического пути. Это время равно разности между поздним и ранним сроками начала или окончания работы.Свободный резерв времени— время, на которое можно увеличить продолжительность работы или перенести ее начало, не изменяя при этом раннего начала последующих работ. Это время равно разности между ранним началом последующей работы и ранним окончанием данной работы. Расчет сетевых графиков можно выполнять в табличной форме или непосредственно на графике. Для расчета в табличной форме события кодируют (нумеруют). Код каждой работы соответствует номерам ее начального и конечного событий. На рис.7,априведен сетевой график строительства жилого дома, трудоемкость и продолжительность работ по которому приведена в табл.3. Фиктивная работа2-3продолжительностью 2 мес. означает ожидание для процесса3-7 («Отделочные работы»).

Источник

3. Определение продолжительности работ

Одним из наиболее важных этапов составления сетевой модели является получение правильных оценок продолжительности работ. Продолжительности работ могут быть определены либо по имеющим­ся нормативам, либо с использованием экспертных вероятностных оценок.

Формулы для определения ожидаемой продолжительности ра­бот вторым методом в зависимости от количества экспертных оценок представлены в табл. 1.

Расчетные зависимости для установления ожидаемой продол­жительности выполнения работ и ее дисперсии на основе экспертных оценок

Наименование параметра

Ожидаемая продолжительность вы­полнения работы

на основе трех экспертных оценок

Ожидаемая продолжительность вы­полнения работы

на основе двух экспертных оценок

Дисперсия (мера разброса) ожидае­мой

продолжительности работы при трех оценках

Дисперсия (мера разброса) ожидае­мой

продолжительности работы при двух оценках

Условные обозначения к таблице:

t_min – минимальная продолжительность работы, выбранная из условия, что выполнение работы будет протекать при наиболее благоприятных обстоятельствах;

t_нв – наиболее вероятная продолжительность работы, выбранная при средних условиях, при которых не возникает никаких неожиданных трудностей;

t_max – максимальная продолжительность работы, выбранная из условия выполнения данной работы при самом неблагоприятном стечении об­стоятельств.

4. Расчет параметров сетевой модели

К основным параметрам сетевой модели относятся характери­стики событий, работ, резервы времени событий и работ. Эти пара­метры являются исходными для получения ряда дополнительных ха­рактеристик, а также для анализа сети или составления плана разра­ботки.

При небольших размерностях сетевой модели (до 100 событий) рассчитываются графическим методом параметры событий, а при больших — табличным методом параметры работ.

Порядок расчета параметров событий

Расчету подлежат следующие параметры:

Т_р – наиболее ранний возможный срок свершения события;

Т_п – наиболее поздний допустимый срок свершения события;

R – резерв времени события.

Расчет выполняется непосредственно на модели. В этом случае событие изображается кружком диаметром 15- 20 мм, разделенным на четыре сектора (рис. 3). Буквой N обозначен номер события.

Расчет выполняется по следующим правилам:

1. Осуществляется проход сетевой модели от исходного собы­тия к завершающему и последовательно определяются ранние срокисвершения событий по формуле:

1. Поздний срок свершения завершающего события принимает­ся равным полученному значению его раннего срока свершения:

1. Осуществляется проход сетевой модели от завершающего со­бытия к исходному и последовательно определяются поздние срокисвершения событий по формуле:

1. Рассчитываются резервы времени всех событий сетевой мо­дели по формуле:

1. Выделяется на сетевой модели (предпочтительно красным цветом) критический путь, как непрерывная последовательность работ от исходного события до завершающего с нулевыми резервами вре­мени событий.

Источник