33. Определение резервов времени сетевой модели.
Сетевая модель – ориентированный граф изображающий все необходимое, для достиж целей операции в технологич-ой взаимосвязи.
Основные элементы сет модели:
2. Событие- результат выполнения 1 или неск-ких работ, позволяющий начинать след работу, изображ-ся в виде круга.
3. Путь- непрерывная послед-ть работ от исходного до завершающего события сетевой модели.
Если из продолжительности критического пути вычесть продолжительность любого другого пути, то получим общий резерв этого пути, т.е. можно увеличить продолжительность работ на этом пути на величину полного резерва, не изменяя продолжительности критического пути.
Но этот резерв нельзя отнести на любую работу, т.к. каждая работа может принадлежать нескольким путям.
Для определения полного резерва, кот можно отнести на данную работу, необходимо рассчитать резервы всех путей, к которым относится данная работа и взять наименьшую величину резерва.
Но это слишком трудоемкий процесс, поэтому используется следующая формула.
Полный резерв показывает, что данную работу можно либо начать позже, либо увеличить продолжительность этой работы на величину резерва.
Использование полного резерва на любую из работ приводят к тому, то эта и все остальные работы данного пути становятся критическими. В результате работе, которая стоит в графике дальше от исходного, может не хватить резервов.
Частный резерв показывает, насколько можно увеличить продолжительность данной работы, либо сдвинуть ее раннее начало, не изменяя как РН последних работ, так и конечного срока графика.
Величина частного резерва не превышает величину полного, а сумма частных резервов всегда равноа полному резерву данного пути.
34. Табличный метод расчета аналитических параметров сетевой модели.
Сетевая модель – ориентированный граф изображающий все необходимое, для достиж целей операции в технологич-ой взаимосвязи.
Основные элементы сет модели:
2. Событие- результат выполнения 1 или неск-ких работ, позволяющий начинать след работу, изображ-ся в виде круга.
3. Путь- непрерывная послед-ть работ от исходного до завершающего события сетевой модели.
1)Для всех работ, выходящих из данного события из данного события раннее начало всегда равно 0.
2) Для определения ранних начал последующих работ необходимо определит ранне окончание предыдщуих.
3) Все работы которые выходят из одного и того же события имеют одно и то же раннее начало.
Определение поздних начал и окончанией производится в обратном порядке.
Позднее окончание работ входящих в одно событие равно.
Определение работ составляющих критический путь.
Критические работы – это работы, лежащие на критическом пути и не имеющие резервов времени.
Некритические работы – это работы не лежащие на критическом пути.
Полный резерв показывает, что данную работу можно либо начать позже, либо увеличить продолжительность этой работы на величину резерва.
Использование полного резерва на любую из работ приводят к тому, то эта и все остальные работы данного пути становятся критическими. В результате работе, которая стоит в графике дальше от исходного, может не хватить резервов.
Частный резерв показывает, насколько можно увеличить продолжительность данной работы, либо сдвинуть ее раннее начало, не изменяя как РН последних работ, так и конечного срока графика.
Величина частного резерва не превышает величину полного, а сумма частных резервов всегда равно полному резерву данного пути.
4 Методы сетевого планирования
Сетевая диаграмма (сеть, граф сети, PERT-диаграмма) — графическое отображение работ проекта и зависимостей между ними. В планировании и управлении проектами под термином «сеть» понимается полный комплекс работ и вех проекта с установленными между ними зависимостями.
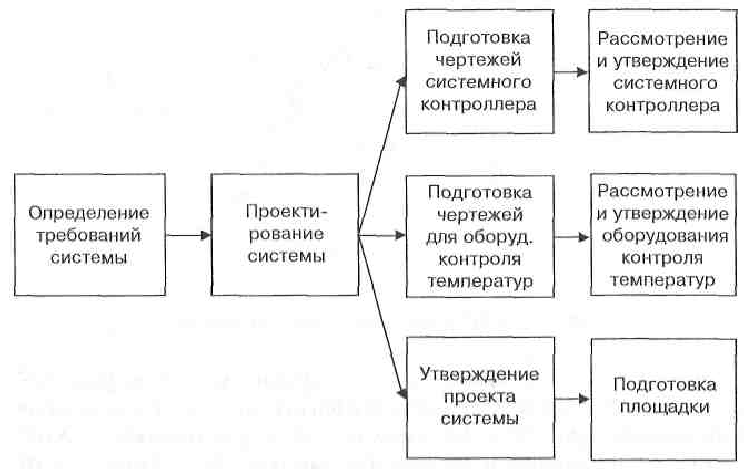
Сетевые диаграммы отображают сетевую модель в графическом виде как множество вершин, соответствующих работам, связанных линиями, представляющими взаимосвязи между работами. Этот граф, называемый сетью типа «вершина—работа» или диаграммой предшествования—следования, является наиболее распространенным представлением сети (рис. 3).
Рис. 3. Фрагмент сети «вершина—работа»
Существует другой тип сетевой диаграммы — сеть типа «вершина—событие», который на практике используется реже. При данном подходе работа представляется в виде линии между двумя событиями (узлами графа), которые, в свою очередь, отображают начало и конец данной работы. PERT- диаграммы являются примерами этого типа диаграмм (рис. 4).
Рис. 4. Фрагмент сети «вершина—событие»
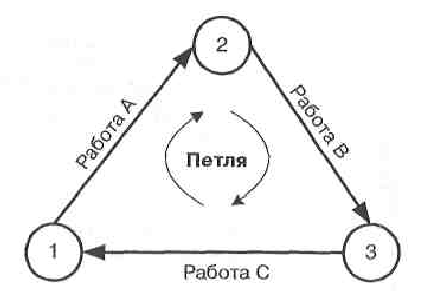
Сетевая диаграмма не является блок-схемой в том смысле, в котором это средство используется для моделирования деловых процессов. Принципиальным отличием от блок-схемы является то, что сетевая диаграмма отображает только логические зависимости между работами, а не входы, процессы и выходы, а также не допускает повторяющихся циклов или так называемых петель (в терминологии графов — ребро графа, исходящее из вершины и возвращающееся в ту же вершину, рис. 5).
Рис.5. Пример петли в сетевой модели
Методы сетевого планирования — методы, основная цель которых заключается в том, чтобы сократить до минимума продолжительность проекта. Основываются на разработанных практически одновременно и независимо методе критического пути МКП (СРМ — Critical Path Method) и методе оценки и пересмотра планов ПЕРТ (PERT — Program Evaluation and Review Technique).
Критический путь — максимальный по продолжительности полный путь в сети называется критическим; работы, лежащие на этом пути, также называются критическими. Именно длительность критического пути определяет наименьшую общую продолжительность работ по проекту в целом.
Длительность выполнения всего проекта в целом может быть сокращена за счет сокращения длительности работ, лежащих на критическом пути. Соответственно любая задержка выполнения работ критического пути повлечет увеличение длительности проекта.
Метод критического пути позволяет рассчитать возможные календарные графики выполнения комплекса работ на основе описанной логической структуры сети и оценок продолжительности выполнения каждой работы, определить критический путь для проекта в целом.
Полный резерв времени, или запас времени, — это разность между датами позднего и раннего окончаний (начал) работы. Управленческий смысл резерва времени заключается в том, что при необходимости урегулировать технологические, ресурсные или финансовые ограничения проекта он позволяет руководителю проекта задержать работу на этот срок без влияния на срок завершения проекта в целом. Работы, лежащие на критическом пути, имеют временной резерв, равный нулю.
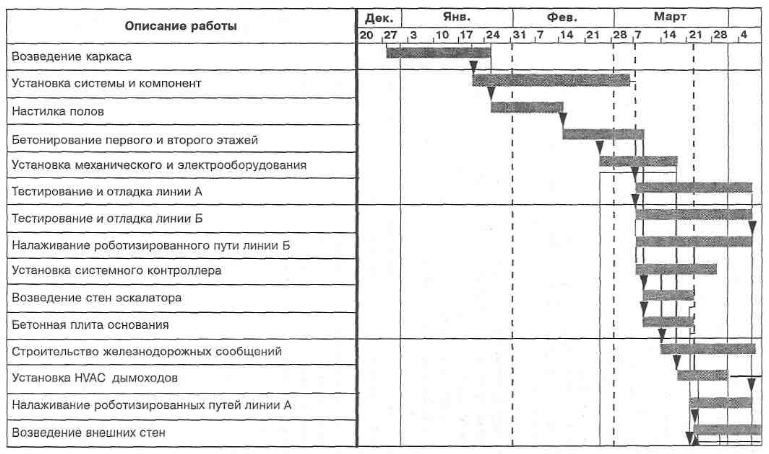
Диаграмма Ганта — горизонтальная линейная диаграмма, на которой задачи проекта представляются протяженными во времени отрезками, характеризующимися датами начала и окончания, задержками и, возможно, другими временными параметрами. Пример отображения диаграммы Ганта с помощью современных компьютерных средств представлен на рис. 6.
Процесс сетевого планирования предполагает, что вся деятельность будет описана в виде комплекса работ или работ с определенными взаимосвязями между ними. Для расчета и анализа сетевого графика используется набор сетевых процедур, известных под названием «процедуры метода критического пути».
Процесс разработки сетевой модели включает в себя:
- определение списка работ проекта;
- оценку параметров работ;
- определение зависимостей между работами.
Определение комплекса работ проводится для описания деятельности по проекту в целом, с учетом всех возможных работ. Работа является основным элементом сетевой модели. Под работами понимается деятельность, которую необходимо выполнить для получения конкретных результатов. Пакеты работ определяют деятельность, которую необходимо осуществить для достижения результатов проекта, которые могут выделяться вехами. Прежде чем начать разработку сетевой модели, необходимо убедиться, что на нижнем уровне СРР определены все работы, обеспечивающие достижение всех частных целей проекта. Сетевая модель образуется в результате определения зависимостей между этими работами и добавления связующих работ и событий. В общем виде данный подход основан на предположении, что каждая работа направлена на достижение частного результата. Связующие работы, возможно, и не требуют получения какого-либо материального конечного результата, например работа «организация исполнения». Оценка параметров работ является ключевой задачей руководителя проекта, привлекающего для решения этой задачи членов команды, ответственных за реализацию отдельных частей проекта. Ценность календарных графиков, стоимостных и ресурсных планов, получаемых в результате анализа сетевой модели, полностью зависит от точности оценок продолжительности работ, а также оценок потребностей работ в ресурсах и финансовых средствах. Оценки должны производиться для каждой детальной работы, а затем могут быть агрегированы и обобщаться по каждому из уровней СРР в плане проекта. Рисунок 6 Диаграмма Ганга
Параметры сетевых моделей и методы их расчета
Сетевая модель имеет ряд характеристик, которые позволяют определить степень напряженности выполнения отдельных работ, а также всего их комплекса и принять решение о перераспределении ресурсов.
Ранний срок наступления события tр(i) — самый ранний из возможных сроков наступления события. Он равен продолжительности максимального пути от исходного события до данного.
tр(i) = max t[Lр(i)] (2.1)
Например, tр(7)=19, т.к. L1=(1,2,4,7), L2=(1,3,4,7),
t(L1)=5+12=17 < t(L2)=7+12=19.
Ранний срок начала работы tр.н.(i,j) равен продолжительности максимального пути от исходного до начального события данной работы.
tр.н.(i,j)=max t[Ln(i)](2.2)
Например, tр.н.(7,11)=19, т.к. L1=(1,2,4,7), L2=(1,3,4,7),
t(L1)=5+12=17
Ранний срок начала работы равен раннему сроку наступления начального события данной работы.
tр.н.(i,j) = tр(i) (2.3)
Ранний срок окончания работы tр.о.( i,j) равен сумме раннего срока начала работы и продолжительности данной работы.
tр.о.(i,j)= tр.н.(i,j) + t(i,j) (2.4)
Например, tр.о.(7,11)= tр.н.(7,11) + t(7,11)= 19+8=27.
Поздний срок наступления события tп( i) равен разности между продолжительностью критического пути и продолжительностью максимального пути от данного события до завершающего.
tп(i) =Tкр — max t[Lк(i)](2.5)
Например, tп(7)=19, т.к. L1=(7,11), L2=(7,9,11), t(L1)=8 > t(L2)=4,
tп(7) = Tкр — max t[Lк(7)]=27 — 8=19.
Для событий критического пути tр( i)=tп(i), для других событий tр(i)tп(i).
Поздний срок окончания работы tп.о.( i,j) – это самый поздний срок окончания работы, при котором планируемый срок окончания проекта не меняется, он равен разности между продолжительностью критического пути и продолжительностью максимального пути от конечного события данной работы до завершающего события.
tп.о.(i,j)=Tкр — max t[Lк(j)] (2.6)
Поздний срок окончания работы равен позднему сроку наступления конечного события tп.о.(i,j) = tп(j). Например, tп.о.(4,7) = tп(7)=19.
Поздний срок начала работы tп.н.( i,j) – самый поздний срок начала работы, при котором планируемый срок окончания проекта не меняется.
tп.н.(i,j)= tп .о.(i,j) — t(i,j) (2.7)
Например, tп.н.(4,7)= tп.о.(4,7) — t(4,7)=19-12=7.
Для работ критического пути ранние и поздние сроки начала и окончания работ равны: tр.н.(4,7)= tп.н.(4,7)=7, tр.о.(4,7)= tп.о.(4,7)=19.
Работы, не лежащие на критическом пути, могут иметь резервы времени.
Полный резерв времени Rп( i,j) – максимальное время, на которое можно увеличить продолжительность данной работы, не изменяя продолжительности критического пути.
Rп (i,j)= tп(j) — tр(i) — t(i,j)
Rп(i,j)= tп.н (i,j) — tр.н.(i,j) (2.8)
Rп (i,j)= tп.о.(i,j) — tр.о.(i,j)
Свободный резерв времени Rс( i,j) равен разности между ранним началом последующей работы и ранним окончанием рассматриваемой работы.
Rс(i,j)= tр.н (j,к) — tр.о.(i,j) (2.9) Перейти к онлайн решению своей задачи