Параметры сетевых моделей и методы их расчета
Сетевая модель имеет ряд характеристик, которые позволяют определить степень напряженности выполнения отдельных работ, а также всего их комплекса и принять решение о перераспределении ресурсов.
Ранний срок наступления события tр(i) — самый ранний из возможных сроков наступления события. Он равен продолжительности максимального пути от исходного события до данного.
tр(i) = max t[Lр(i)] (2.1)
Например, tр(7)=19, т.к. L1=(1,2,4,7), L2=(1,3,4,7),
t(L1)=5+12=17 < t(L2)=7+12=19.
Ранний срок начала работы tр.н.(i,j) равен продолжительности максимального пути от исходного до начального события данной работы.
tр.н.(i,j)=max t[Ln(i)](2.2)
Например, tр.н.(7,11)=19, т.к. L1=(1,2,4,7), L2=(1,3,4,7),
t(L1)=5+12=17
Ранний срок начала работы равен раннему сроку наступления начального события данной работы.
tр.н.(i,j) = tр(i) (2.3)
Ранний срок окончания работы tр.о.( i,j) равен сумме раннего срока начала работы и продолжительности данной работы.
tр.о.(i,j)= tр.н.(i,j) + t(i,j) (2.4)
Например, tр.о.(7,11)= tр.н.(7,11) + t(7,11)= 19+8=27.
Поздний срок наступления события tп( i) равен разности между продолжительностью критического пути и продолжительностью максимального пути от данного события до завершающего.
tп(i) =Tкр — max t[Lк(i)](2.5)
Например, tп(7)=19, т.к. L1=(7,11), L2=(7,9,11), t(L1)=8 > t(L2)=4,
tп(7) = Tкр — max t[Lк(7)]=27 — 8=19.
Для событий критического пути tр( i)=tп(i), для других событий tр(i)tп(i).
Поздний срок окончания работы tп.о.( i,j) – это самый поздний срок окончания работы, при котором планируемый срок окончания проекта не меняется, он равен разности между продолжительностью критического пути и продолжительностью максимального пути от конечного события данной работы до завершающего события.
tп.о.(i,j)=Tкр — max t[Lк(j)] (2.6)
Поздний срок окончания работы равен позднему сроку наступления конечного события tп.о.(i,j) = tп(j). Например, tп.о.(4,7) = tп(7)=19.
Поздний срок начала работы tп.н.( i,j) – самый поздний срок начала работы, при котором планируемый срок окончания проекта не меняется.
tп.н.(i,j)= tп .о.(i,j) — t(i,j) (2.7)
Например, tп.н.(4,7)= tп.о.(4,7) — t(4,7)=19-12=7.
Для работ критического пути ранние и поздние сроки начала и окончания работ равны: tр.н.(4,7)= tп.н.(4,7)=7, tр.о.(4,7)= tп.о.(4,7)=19.
Работы, не лежащие на критическом пути, могут иметь резервы времени.
Полный резерв времени Rп( i,j) – максимальное время, на которое можно увеличить продолжительность данной работы, не изменяя продолжительности критического пути.
Rп (i,j)= tп(j) — tр(i) — t(i,j)
Rп(i,j)= tп.н (i,j) — tр.н.(i,j) (2.8)
Rп (i,j)= tп.о.(i,j) — tр.о.(i,j)
Свободный резерв времени Rс( i,j) равен разности между ранним началом последующей работы и ранним окончанием рассматриваемой работы.
Rс(i,j)= tр.н (j,к) — tр.о.(i,j) (2.9) Перейти к онлайн решению своей задачи
8.3. Расчет сетевой модели
Расчет параметров может вестись различными методами (аналитическими, в табличной форме, по графику) вручную или с применением компьютеров.
Рассмотрим пример (рис.4.) расчета сетевого графика табличным методом. Продолжительность критического пути определяется при рассмотрении всех путей последовательно выполняемых работ от исходного события до конечного (табл.1).
3
3
1 1 3
2
Рис.4. Схема сетевого графика
Расчет критического пути по сетевому графику
Суммирование продолжительности работ по путям сетевого графика
Суммирование продолжительности работ по путям сетевого графика
Из табл.1 видно, что наибольшую продолжительность имеет цепочка работ, ограниченная событиями 1,2,5,6,8. Она равна 16 дн. (или в других единицах времени).
Рассмотрим на примере одной работы определение других параметров сетевого графика.
Раннее начало работы – это самый ранний из возможных сроков начала работы с учетом сроков выполнения предшествующих работ.
Раннее начало работы определяется продолжительностью самого длинного пути от начального события до начала работы по формуле
где ∑ th-і , — максимальная продолжительность всех работ от начального события до начала данной работы.
Раннее окончание работы – это срок окончания работы при условии ее начала в самый ранний из возможных сроков. Раннее окончание работы определяется путем суммирования раннего начала и продолжительности данной работы по формуле
Позднее начало работы – это самый поздний срок, при котором может быть начата работа без нарушения продолжительности критического пути, т.е. общего срока выполнения программы.
Позднее начало определяется разностью критического пути и суммы продолжительности данной работы и самого длинного пути от конечного события до события, стоящего у конца данной работы, по формуле
где ∑ tј-k — максимальная продолжительность от завершающего события до окончания данной работы.
Позднее окончание работы – это предельно допустимый срок, в который может быть окончена данная работа без увеличения продолжительности критического пути. Позднее окончание равно сумме позднего начала и продолжительности данной работы и определяется по формуле
После расчета ранних и поздних начал и окончаний можно определить резервы времени, которые имеются при выполнении отдельных работ при общей продолжительности строительства, равной критическому пути.
Общий запас времени – это время, на которое можно перенести начало работы или увеличить ее продолжительность, не нарушая общего срока выполнения программы. Общий запас определяется разностью позднего и раннего начала или позднего и раннего окончания работ по формулам:
Частный запас времени – это время, на которое можно перенести начало работы или увеличить ее продолжительность без изменения раннего начала последующих работ. Частный запас определяется как разность раннего начала последующей работы и раннего окончания данной работы
где tі-k — раннее начало последующей работы; tі-ј — раннее окончание данной работы.
Расчет начинается с записи в табл.2 перечня работ и их продолжительности
Результаты расчета сетевого графика
1.3.5. Пример построения и расчета сетевой модели
Исходные данные варианта лабораторной работы включают название и продолжительность каждой работы (табл. 1.1), а также описание упорядочения работ.
- Работы C, I, Gявляются исходными работами проекта, которые могут выполняться одновременно.
- Работы E иAследуют за работойC.
- Работа Hследует за работойI.
- Работы D иJследуют за работойG.
- Работа Bследует за работойE.
- Работа Kследует за работамиAиD, но не может начаться прежде, чем не завершится работаH.
- Работа Fследует за работойJ.
На рис.1.4 представлена сетевая модель, соответствующая данному упорядочению работ. Каждому событию присвоен номер, что позволяет в дальнейшем использовать не названия работ, а их коды (см. табл. 1.2). Численные значения временных параметров событий сети вписаны в соответствующие секторы вершин сетевого графика, а временные параметры работ сети представлены в табл. 1.3. Таблица 1.2 Описание сетевой модели с помощью кодирования работ
| Номера событий | Код работы | Продолжительность | |
| начального | конечного | работы | |
| 1 | 2 | (1,2) | 4 |
| 1 | 3 | (1,3) | 3 |
| 1 | 4 | (1,4) | 5 |
| 2 | 5 | (2,5) | 7 |
| 2 | 6 | (2,6) | 10 |
| 3 | 6 | (3,6) | 8 |
| 4 | 6 | (4,6) | 12 |
| 4 | 7 | (4,7) | 9 |
| 5 | 8 | (5,8) | 8 |
| 6 | 8 | (6,8) | 10 |
| 7 | 8 | (7,8) | 11 |
Рис.1.4. Сетевая модель Таблица 1.3 Временные параметры работ
 |  |  |  |  |  |  |  |
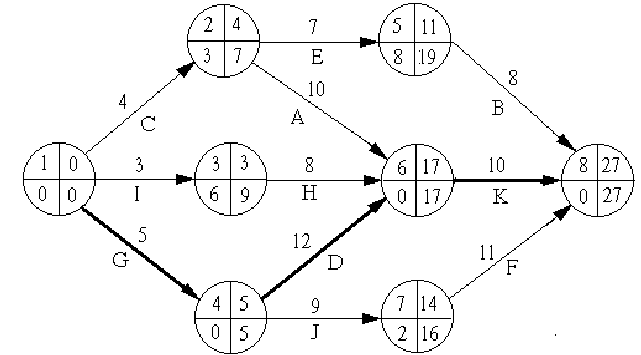
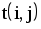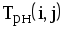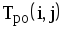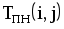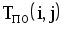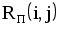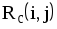| 1,2 | 4 | 0 | 4 | 3 | 7 | 3 | 0 |
| 1,3 | 3 | 0 | 3 | 6 | 9 | 6 | 0 |
| 1,4 | 5 | 0 | 5 | 0 | 5 | 0 | 0 |
| 2,5 | 7 | 4 | 11 | 12 | 19 | 8 | 0 |
| 2,6 | 10 | 4 | 14 | 7 | 17 | 3 | 3 |
| 3,6 | 8 | 3 | 11 | 9 | 17 | 6 | 6 |
| 4,6 | 12 | 5 | 17 | 5 | 17 | 0 | 0 |
| 4,7 | 9 | 5 | 14 | 7 | 16 | 2 | 0 |
| 5,8 | 8 | 11 | 19 | 19 | 27 | 8 | 8 |
| 6,8 | 10 | 17 | 27 | 17 | 27 | 0 | 0 |
| 7,8 | 11 | 14 | 25 | 16 | 27 | 2 | 2 |
1.4. Контрольные вопросы
1.4.1. Зачетный минимум
- Определение события, виды событий, практические примеры событий, обозначение событий на графике, временные параметры событий.
- Определение работы, классификация работ с приведением соответствующих практических примеров, обозначение работ на графике, временные параметры работ.
- Правила построения сетевых графиков.
- Определение пути в сетевом графике, виды путей, важность определения критического пути.
- Умение вычислять временные параметры событий и работ.
1.4.2. Дополнительные вопросы
- Почему при расчете раннего срока свершения события iвыбираютмаксимальнуюиз сумм
? - Почему при расчете позднего срока свершения события iвыбираютминимальнуюиз разностей ?
- Какова взаимосвязь полного и свободного резервов работы?
- Как можно найти критических путь в сетевой модели, без непосредственного суммирования длительностей работ?
?
? Часть 2. ОПТИМИЗАЦИЯ СЕТЕВЫХ МОДЕЛЕЙ ПО КРИТЕРИЮ «МИНИМУМ ИСПОЛНИТЕЛЕЙ» 2.1. ЦЕЛЬ РАБОТЫ Знакомство с методикой и приобретение навыков проведения оптимизации сетевых моделей по критерию «Минимум исполнителей». 2.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Согласно номеру своего варианта получите данные о количество исполнителей, занятых на каждой работе сетевой модели, и ограничение по численности Nодновременно занятых в работе исполнителей. 2. Постройте в отчете графики привязки и загрузки, используя нормальные длительности работ сети — 
(см. п.2.3.1), и покажите их преподавателю. 3. Проверьте правильность построения графиков привязки и загрузки с помощью компьютера, в случае необходимости выявите и устраните ошибки. 4. Используя компьютерную программу, проведите уменьшение численности исполнителей, одновременно занятых на работах сети, до требуемого уровня N. 5. Отчет по лабораторной работе должен содержать:
- номер варианта;
- исходные данные варианта;
- графики привязки и загрузки до проведения оптимизации загрузки;
- графики привязки и загрузки после проведения оптимизации загрузки (возможно использование пунктирных линий на первоначально построенных графиках для отображение изменений в привязке работ и загрузке сети, вызванных сдвигами работ);
- коды работ, сдвинутых в процессе оптимизации, и время их сдвига.
2.3. Алгоритм расчета параметров детерминированной сетевой модели
Расчет параметров сетевого графа можно выполнить непосредственно по графику, таблично и на ЭВМ.
Расчет параметров событий непосредственно по графику состоит из следующих этапов:
1.Каждое событие на графе изображается кругом, разделенным на 4 сектора.
— раннее время наступления i- го события (левый сектор).
— позднее время наступления i- го события (правый сектор).
В нижнем секторе проставляют номер предыдущего события.
Рис.2.3. Пример сетевого графа
2. Нумеруют события, применяя метод вычеркивания дуг. Проставляют номер события в верхнем секторе.
3. В левый сектор заносят раннее время наступления события, в нижний – номер того события, через которое к данному событию проходит максимальный по продолжительности путь.
4. В правый сектор записывают позднее время наступления события.
5. Выделяют критический путь, используя свойство работ, лежащих на критическом пути:
а) ;
б) критические работы связывают данное событие с предыдущим, номер которого указан в нижнем секторе.
Рассмотрим расчет параметров событий сетевой модели «Работы-события» на примере сетевого графа.
Требуется рассчитать параметры сетевого графа (рис.2.3) и по нему определить критический путь.
Рис.2.4. Расчет параметров событий
Исходному событию присваивают номер 0 или 1. Вычеркивают работы выходящие из нулевого события и нумеруют сверху вниз (можно снизу вверх) события 1 и 2. Затем вычеркивают работы выходящие из первого события и нумеруют событие 3. Вычеркивая из второго события, выходящие работы, получают 4 и 5 событие и т.д., двигаясь по порядку номеров, получают последнее завершающее событие с номером 10.
Получили цепочку событий 
, образующих критический путь длиной 
=27. Критический путь обозначен на рисунке (Рис.2.3) двойными стрелками.
Расчет параметров работ сетевой модели «Работы-события»
Работы в таблицу заносятся в лексикографическом порядке. В начале записывают работы с меньшим номером начала. Если две работы имеют общее начало, то раньше заносится та работа, у которой меньше номер конца.
1 столбец i — номер начала работы;
2 столбец j — номер конца работы;
3 столбец — продолжительность работы;
4 столбец — время раннего наступления работ, причем время раннего наступления работ, выходящих из исходного события, равно 0.
Как только известно, раннее начало работы, сразу же вычисляется ее раннее окончание: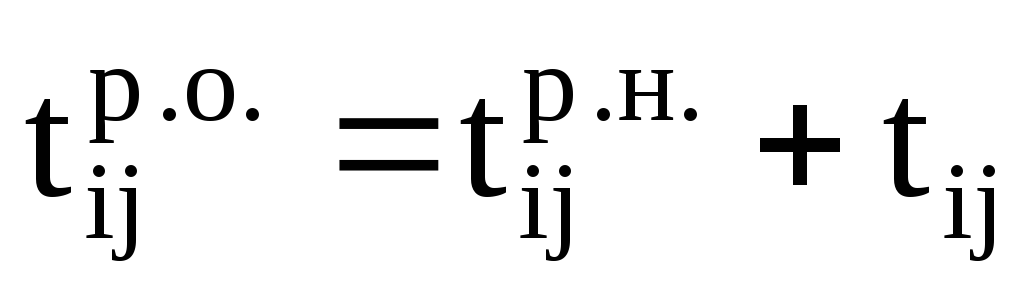 
, 
.
5 столбец — время раннего окончания работы;
6 столбец — время позднего наступления работ;
7 столбец — время позднего окончания работ.
6 и 7 столбцы заполняются “ снизу — вверх ”.
Срок позднего окончания работ заканчивается завершающим событием, т. е. равен длине критического пути. Если же известен срок позднего окончания работы, то срок позднего наступления работы вычисляется по формуле:
, 
.
8 столбец — полный резерв работы. .
9 столбец – работы критического пути.
Работы с нулевыми резервами образуют критический путь.
10 столбец – свободный резерв.
11 столбец – 
потребное количество ресурсов для выполнения 
работы. Например, количество трудовых ресурсов на графе обычно указывают в скобках 2(5), т.е. два дня работают пять человек.
Расчет параметров работ сетевого графа, изображенного на рис.2.3, представлен в таблице 2.1.
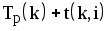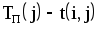