Расчет сетевой модели алгоритм

1.4.Расчет сетевой модели

Классическим видом сетевой модели является детерминированная (строго определенная) сетевая модель, у которой совокупность взаимосвязанных работ (топология) и количественные оценки (продолжительности по времени выполнения работ – метрика) строго и однозначно определены:

i– код начала работы,j- код окончания работы;

t(ij) – время выполнения работы (дни, часы, недели, месяцы и пр.).

Целью построения сетевой модели является ее расчет. В результате расчета получаются количественные характеристики (параметры) событий и работ, которые показывают календарное время наступления событий, время начала и окончания работ и общее время выполнения всего комплекса работ от i₀доi_n.

Топология сетевой модели позволяет рассчитывать для каждого события и работы две возможности – раннегоипозднегосрока наступления и начала работ. Существует ряд методов решения поставленной задачи. Как показывают исследования, наиболее приемлемым являетсяунифицированный алгоритм Форда.

1.4.1.Временные параметры событий сетевой модели

Ранний срок наступления событийхарактеризует самое раннее возможное наступление любого событияiотносительно времени наступленияi₀. Согласно алгоритму Форда ранний срок наступления события можно определить в варианте прямой прогонки сетевой модели (отi₀доi_n), в основе которого лежит соотношение (1.1)

0, если i = i₀

По формуле (1.1) рассчитываются ранние сроки наступления всех событий сетевой модели. Необходимо иметь в виду, что для расчета надо учитывать порядок предшествования.

Полученные i> для всех событий представляют собой абсолютные значения времени наступления событий, т.е. через сколько единиц времени наступит событиеi, начиная от точкиi₀. Для перевода сроков наступления событий в календарные даты необходимо задать дату наступления исходного календарного события сетевой модели.

Значение Т p _iпоказывает длину максимального пути, предшествующего событиюi–t[L_{max предш}(i)]. Следовательно, значение Т p _inпоказывает самый длинный по продолжительности путь в сетевой модели; он называетсякритическим путем Ткри показывает минимально возможное время выполнения всех работ сетевой модели. Указанное соображение характеризуется рисунком 1.8.

Рис.1.8.Фрагмент сетевой модели

Событию iпредшествуют следующие пути:

1. I₀-1 –2 –i(длина пути равна 16)
2. I₀— 3 –i(длина пути равна 9)
3. I₀— 4 –i(длина пути равна 27)

Следовательно, t[L_{max предш}(i)] = 27. Если рассчитать сетевую модель по алгоритму Форда, то Т p _i= 27. Заметим, что алгоритм Форда не использует «перебор» путей, а направленно рассматривает только те работы, которые непосредственно входят в данное событие (См. фрагмент, изображенный на рисунке 1.9.) Рис.1.9.Фрагмент, характеризующий связь «событие – то, что ему непосредственно предшествует». Поздний срок наступления событийхарактеризует самое позднее время наступления событияi. Расчет поздних сроков наступления событий осуществляется в варианте обратной прогонки алгоритма Форда (отi_nдоi₀) по соотношению(1.2) Т p ,если i=i_n Т п _i = min [T n _j -t(ij) ,если i≠i_n (1.2) ijЄU и _i Согласно алгоритму Форда и формуле (1.2) для каждого события рассматривается фрагмент, изображенный на рис.1.10. Рис.1.10. Фрагмент, характеризующий связь «событие – то, что из него непосредственно исходит» Резерв времени событияхарактеризует запас времени события (в днях), учитывающий возможность перенести срок наступления события, не изменяя при этом срока наступления завершающего событияi_n(т.е. Ткр), и рассчитывается по формуле (1.3) R (i) = T п _i –T p _i (1.3) Рассмотрим пример расчета сетевой модели Исходная информация для построения топологии сетевой модели и продолжительности работ дана в таблице 1.2. Сетевая модель (рис.1.11) отображает процесс маркетингового исследования фирмы, желающей выйти со своим товаром на рынок. Цель расчета – определить окончательный срок исследования и календарные даты наступления событий и сроков начала и окончания работ. Таблица 1.2. Исходная информация

Код работы i-j	Наименование работы	Продолжительность работы (i-j), дни
1-2	Исследование внутреннего рынка	3
1-4	Исследование зарубежного рынка	7
2-4	Определение сегмента внутреннего рынка	4
4-6	Определение политики освоения сегментов внутреннего и зарубежного рынков	2
1-5	Исследование качества выпускаемого товара	5
5-4	Разработка программы по адаптации товара к сегментам рынка	8
5-7	Разработка рекламной политики по продвижению товара на рынке	3
2-3	Разработка программы услуг по передвижению товара	6
3-6	Выбор посредников	2
7-6	Разработка политики оптовой и розничной торговли	10
8-8	Разработка торговой марки и упаковки	4
6-8	Определение ценовой политики	7
7-8	Разработка программы сервисного обслуживания	8

6 Рис.1.11.Сетевая модель, отображающая процесс маркетингового исследования Произведем расчет параметров T p _i,T п _iиR(i). РасчетTp_i: T p _io = T p ₁ = 0 T p ₂ = T p ₁ + t(1-2) = 0+3 = 3 T p ₅ = T p ₁ + t(1-5) = 0+5 = 5 T p ₄ =max [T p ₂ + t(2-4); T p ₅ + t(5-4); T p ₁ + t(1-4)] = max [3+4; 5+8; 0+7] = 13 2-4 5-4 1-4 T p ₃ = T p ₂ + t(2-3) = 3+6 =9 T p ₇ = T p ₅ + t(5-7) =5+3 = 8 T p ₆ = max [T p ₃ + t(3-6); T p ₄ + t(4-6); T p ₇ + t(7-6)] = max [9+2; 13+2; 8+10] = 18 3-6 6-8 7-6 T p ₈ = max [T p ₃ + t(3-8); T p ₆ + t(6-8); T p ₇ + t(7-8)] = max [9+4; 18+7; 8+8] = 25 3-8 6-8 7-8 Следовательно, Ткр = Т р ₈= 25. Это означает, что все работы сетевой модели по маркетинговому исследованию могут быть выполнены не менее, чем за 25 дней. Расчет Тп_i: T п _io =T п ₈= 25 T п ₆= Т п ₈–t(6-8) = 25-7 = 18 T п ₇ = min [T п ₆ – t(7-6); T п ₈ – t(7-8)] = min [18-10; 25-8] = 8 7-6 7-8 T п ₃ = min [T п ₈ – t(3-8); T п ₆ – t(3-6)] = min [25-4;18-2] = 16 3-8 3-6 T п ₄ = T п ₆ – t(4-6) = 18-2 = 16 T п ₅ = min [T п ₄ – t(5-4); T п ₇ – t(5-7)] = min[16-8; 8-3] = 5 5-4 5-7 T п ₂ = min [T п ₃ – t(2-3); T п ₄ – t(2-4)] = min [16-6; 16-4] = 10 2-3 2-4 T п ₁ = min [T п ₂ – t(1-2); T п ₄ – t(1-4); T п ₅ – t(1-5)] = min [10-3; 16-7; 5-5] = 0 1-2 1-4 1-5 Если задать дату исходного события, то можно получить календарные даты наступления каждого события. Пусть дата i₀будет 1.01.2001г. Будем считать, что все дни – рабочие. (Если учитывать праздничные и выходные дни, то их надо удалить из рассматриваемой шкалы). Тогда результаты расчета можно свести в таблицу 1.3. Таблица 1.3. Временные параметры и резервы времени событий

Код события i	Ранний срок наступления события Т р i	Поздний срок наступления события Т п i	Резерв времени события R (i)
1	0	0	0
	1.01.2001.	1.01.2001.
2	3	10	7
	3.01.2001.	10.01.2001.
5	5	5	0
	5.01.2001.	5.01.2001.
4	13	16	3
	13.01.2001.	16.01.2001.
3	9	16	5
	9.01.2001.	16.01.2001.
7	8	8	0
	8.01.201.	08.01.2001.
6	18	18	0
	18.01.2001.	18.01.2001.
8	25	25	0
	25.01.2001.	25.01.201.

Алгоритм Форда дает возможность рассмотреть некоторые теоретические положения, которые мы сформулируем в виде теорем (без доказательств) и которые будем Теорема 1.Длина критического пути в сетевой модели равна величине Т п _io: т.е. Ткр = t[L_{maxпредш}(i_n)] =T p _in=T п _in. (1.4) Теорема 2.Длина максимального пути, следующего за некоторой вершинойi, равна разности Ткр и соответствующей величины Т п _i: т.е. t[L_maxслед(i)] = Ткр – Т п _i(1.5) Теорема 3.Если некоторая величинаiпринадлежит критическому пути, то величины Т р _iи Т п _i равны между собой: т.е. iЄLкр => Т р _i=T п _iТеорема 4. Если событие принадлежит критическому пути, то резерв данного события равен 0: т.е. i Є Lкр => R(i) = 0 Обратимся к таблице 1.3. События 1, 5, 7, 6, 8 принадлежат критическому пути

Источник

1.3.5. Пример построения и расчета сетевой модели

Исходные данные варианта лабораторной работы включают название и продолжительность каждой работы (табл. 1.1), а также описание упорядочения работ.

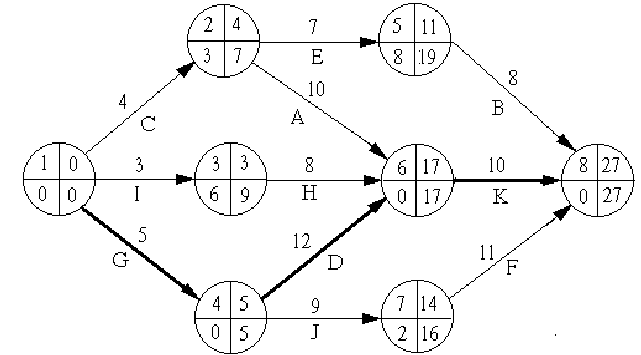
1. Работы C, I, Gявляются исходными работами проекта, которые могут выполняться одновременно.
2. Работы E иAследуют за работойC.
3. Работа Hследует за работойI.
4. Работы D иJследуют за работойG.
5. Работа Bследует за работойE.
6. Работа Kследует за работамиAиD, но не может начаться прежде, чем не завершится работаH.
7. Работа Fследует за работойJ.

На рис.1.4 представлена сетевая модель, соответствующая данному упорядочению работ. Каждому событию присвоен номер, что позволяет в дальнейшем использовать не названия работ, а их коды (см. табл. 1.2). Численные значения временных параметров событий сети вписаны в соответствующие секторы вершин сетевого графика, а временные параметры работ сети представлены в табл. 1.3. Таблица 1.2 Описание сетевой модели с помощью кодирования работ

Номера событий		Код работы	Продолжительность
начального	конечного	работы
1	2	(1,2)	4
1	3	(1,3)	3
1	4	(1,4)	5
2	5	(2,5)	7
2	6	(2,6)	10
3	6	(3,6)	8
4	6	(4,6)	12
4	7	(4,7)	9
5	8	(5,8)	8
6	8	(6,8)	10
7	8	(7,8)	11

Рис.1.4. Сетевая модель Таблица 1.3 Временные параметры работ

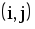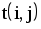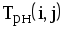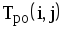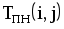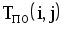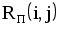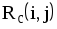1,2	4	0	4	3	7	3	0
1,3	3	0	3	6	9	6	0
1,4	5	0	5	0	5	0	0
2,5	7	4	11	12	19	8	0
2,6	10	4	14	7	17	3	3
3,6	8	3	11	9	17	6	6
4,6	12	5	17	5	17	0	0
4,7	9	5	14	7	16	2	0
5,8	8	11	19	19	27	8	8
6,8	10	17	27	17	27	0	0
7,8	11	14	25	16	27	2	2

1.4. Контрольные вопросы

1.4.1. Зачетный минимум

1. Определение события, виды событий, практические примеры событий, обозначение событий на графике, временные параметры событий.
2. Определение работы, классификация работ с приведением соответствующих практических примеров, обозначение работ на графике, временные параметры работ.
3. Правила построения сетевых графиков.
4. Определение пути в сетевом графике, виды путей, важность определения критического пути.
5. Умение вычислять временные параметры событий и работ.

1.4.2. Дополнительные вопросы

1. Почему при расчете раннего срока свершения события iвыбираютмаксимальнуюиз сумм ?
2. Почему при расчете позднего срока свершения события iвыбираютминимальнуюиз разностей ?
3. Какова взаимосвязь полного и свободного резервов работы?
4. Как можно найти критических путь в сетевой модели, без непосредственного суммирования длительностей работ?

Часть 2. ОПТИМИЗАЦИЯ СЕТЕВЫХ МОДЕЛЕЙ ПО КРИТЕРИЮ «МИНИМУМ ИСПОЛНИТЕЛЕЙ» 2.1. ЦЕЛЬ РАБОТЫ Знакомство с методикой и приобретение навыков проведения оптимизации сетевых моделей по критерию «Минимум исполнителей». 2.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Согласно номеру своего варианта получите данные о количество исполнителей, занятых на каждой работе сетевой модели, и ограничение по численности Nодновременно занятых в работе исполнителей. 2. Постройте в отчете графики привязки и загрузки, используя нормальные длительности работ сети — 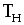(см. п.2.3.1), и покажите их преподавателю. 3. Проверьте правильность построения графиков привязки и загрузки с помощью компьютера, в случае необходимости выявите и устраните ошибки. 4. Используя компьютерную программу, проведите уменьшение численности исполнителей, одновременно занятых на работах сети, до требуемого уровня N. 5. Отчет по лабораторной работе должен содержать:

• номер варианта;
• исходные данные варианта;
• графики привязки и загрузки до проведения оптимизации загрузки;
• графики привязки и загрузки после проведения оптимизации загрузки (возможно использование пунктирных линий на первоначально построенных графиках для отображение изменений в привязке работ и загрузке сети, вызванных сдвигами работ);
• коды работ, сдвинутых в процессе оптимизации, и время их сдвига.

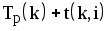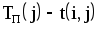Источник