6.2. Расчет сетевых моделей
Исходные данные для расчета сетевой модели. Наиболее важным параметром является время выполнения работы, поскольку с ним взаимосвязаны такие характеристики как объемы и способы работ, денежные и трудовые затраты, расход материалов и др. В СПУ рекомендуется оценку продолжительности операций поручить исполнителю, при этом без взаимосвязи с общими сроками по программе. Каждая работа может быть оценена с различной степенью уверенности. При этом продолжительность работы рассматривается как случайная величина, зависящая от большого числа факторов и представляющая собой ассиметричную функцию распределения (чаще всего в виде бетта-распределения).
Надо помнить, что оценки — не календарные сроки выполнения работ.
Расчетные параметры сетевой модели. Расчетные параметры сети повышают качество принимаемых решений при планировании и управлении реальными процессами.
Расчетные параметры можно отнести либо к событию, либо к работе.
Параметры, характеризующие работы, такие как ранний срок начала работы, ранний срок окончания работы, поздний срок начала работы, поздний срок окончания работы и полный, свободный первый частный, второй частный резервы времени на работе
К параметрам, характеризующим события, относятся следующие.
— ранний срок свершения события Тр(m);
— поздний срок свершения события Тn(m);
— резерв времени свершения события R(m).
Тр (m) – определяется продолжительностью самого длинного пути ведущего от исходного события в данное. Для его нахождения необходимо ко всем ранним срокам свершения предшествующих событий, начиная с исходного, прибавить соответствующие продолжительности работ и из полученных сумм взять наибольшую. При этом для исходного события ранний срок его свершения равен нулю, т.е. Тр(m) = 0.
Ранний срок свершения завершающего события Тр(N) определяется продолжительностью выполнения всего проекта. Путь от исходного события до завершающего, определяющий Тр(N), называется критическим путем. Их может быть несколько. Может быть и так, что удлинение некритического пути изменит ситуацию и критический путь пройдет по-иному. Укорачивание критического пути может привести к тому же. Удлинение критического пути сдерживает все работы и увеличивает продолжительность реализации всего проекта.
Тn(m) – определяется как разность между продолжительностью критического пути и продолжительностью самого длинного пути, ведущего от данного события в завершающее.
Для расчета Тn(m) необходимо из всех поздних сроков свершения последующих событий вычесть соответствующие продолжительности работ и из полученных разностей взять наименьшую. Расчет поздних сроков свершения событий начинается последовательно от завершающего события, для которого поздний срок его свершения принимается равным раннему сроку завершающего события, т.е.Тn(N) = Тр (N).
Поздний срок исходного события должен быть равным раннему сроку, т.е. иметь нулевое значение, что является одним из средств проверки правильности расчета сети. Резерв времени свершения события R(m) — это запас времени межу ранним и поздним сроком свершения данного события. Для каждого события R(m) определяется как разность между поздним сроком свершения и ранним сроком его свершения:
R(m) = Тn(m) – Тр(m).
Если при расчете приняли, что срок свершения завершающего события равен раннему сроку его свершения, то резерв времени завершающего события будет равен нулю, т.е. R(I) = 0. Более того, для всех событий лежащих на критическом пути резерв времени по событию равен нулю. Для остальных событий сети их резерв будет иметь положительную величину. Данное положение может быть использовано при организации работ по проекту, т.к. увеличение продолжительности работ при положительном значении резерва по событию не скажется на положении критического пути. И наоборот, увеличение продолжительности работ свыше положительного резерва времени по событию может изменить направление критического пути.
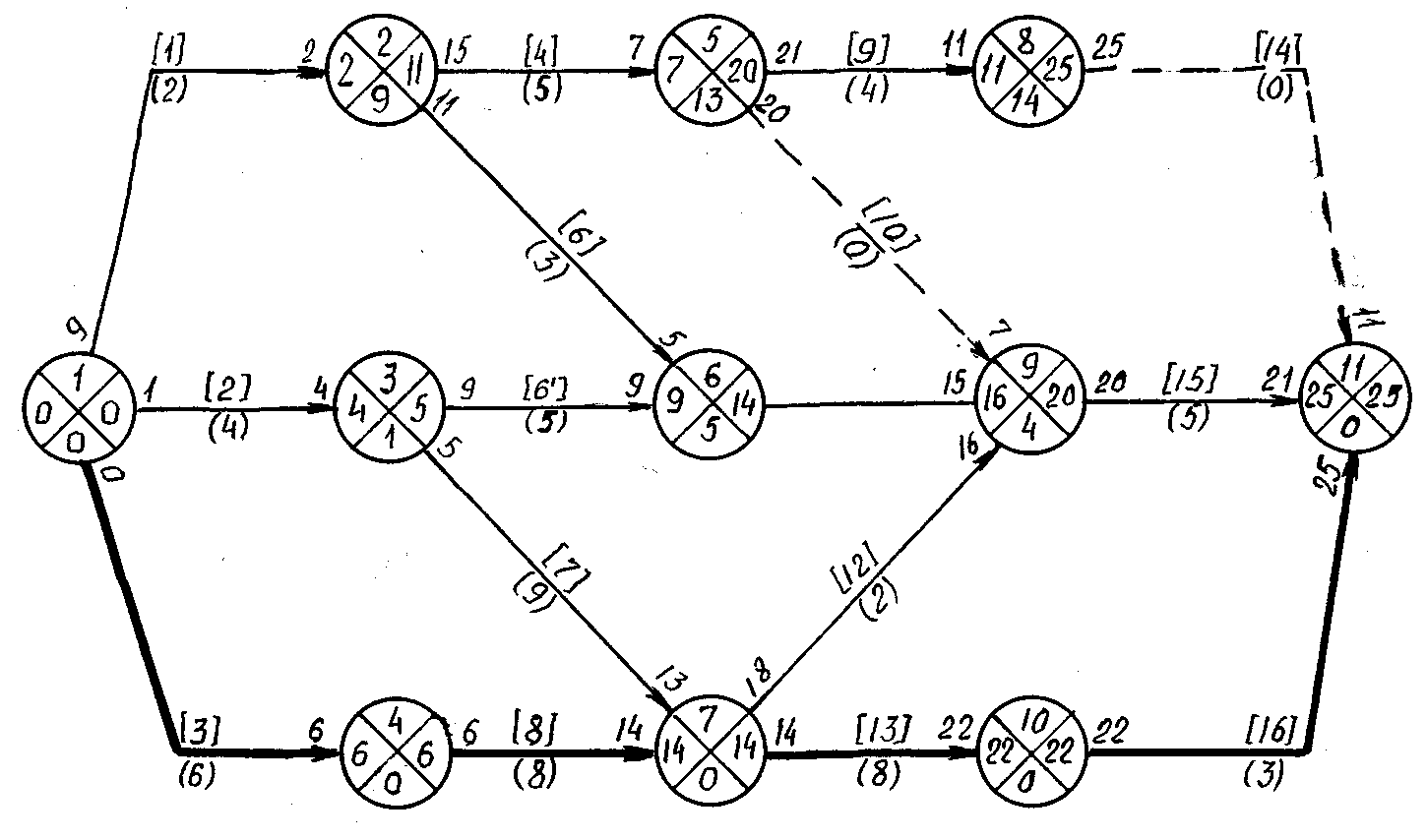
Расчет сетевой модели на графе. В методе расчета непосредственно на сети кружки событий делаются несколько большими с таким расчетом, чтобы в их секторах можно было вписать цифровые данные. Рис.7.1.
Рис. 6.1. Параметры сетевой модели, используемые при расчете сети на графе
Рис. 6.2. Сетевая модель с результатами расчета на графе
Расчет параметров сети осуществляется в следующем порядке.(Рис.7.2.)
1. Расчет раннего срока свершения событий в сети. Он осуществляется в направлении от исходного события в завершающее событие, переходя последовательно от одного события к другому. При этом ранний срок свершения исходного события принимаем равным нулю, т.е. Тр(1) = 0.
а). Ранний срок свершения событий Тр(m) определяется по максимальному значению раннего окончания всех ему предшествующих работ и записывается в левом секторе соответствующего кружка.
б). Раннее окончание работы равно сумме раннего начала соответствующей работы и продолжительности самой работы. Значение раннего окончания работы записывается над стрелкой у ее конца. Раннее начало работы равно раннему сроку свершению предшествующего события. Оно записывается внизу у начала стрелки-работы.
2. Расчет позднего срока свершения событий в сети. Он осуществляется в направлении от завершающего события к исходному событию, переходя последовательно от одного события к другому. При этом поздний срок свершения завершающего события принимаем равным раннему сроку свершения завершающего события, т.е. Тn(N) = Тр(N)
а). Поздний срок свершения события Тn(m) определяется по наименьшему значению позднего начала всех для него последующих работ и записывается в правом секторе кружка.
б). Позднее начало работы равно разности позднего ее окончания и продолжительности самой работы. Значение позднего начала работы записывается над стрелкой у ее начала. Позднее начало работы равно позднему сроку свершения предшествующего ей события и записывается под стрелкой-работой у ее конца.
3. Расчет резерва времени по событию. Значение резерва времени по событию R(m) для всех событий определяется по формуле:
R(m) = Тn(m) – Тр(m)
4. Определение критического пути.
Если Тn(N) = Тр(N), то критический путь пройдет через события, для которых резерв времени равен нулю, т.е. R(m) = 0. Остальные расчетные параметры, при необходимости, определяются по соответствующим формулам и сводятся в таблицу или выносятся на сеть.
Задания по формированию навыков
составления и расчета сетевых моделей для индивидуальной и групповой работы выдаются руководителем практических занятий в виде чертежного изображения системы разработки.
Вопросы для самоконтроля знаний
Пояснить состав работ и событий в сетевой модели
Назвать содержание цикла масштабного представления сети
Назвать отличия сетевой модели от линейного графика Ганта
Пояснить смысл вероятностной оценки продолжительности работ
Указать состав кода работы и события
Привести расчетные параметры, характеризующие работу
Пояснить сущность критического пути в сетевой модели
Привести расчетные параметры, характеризующие событие
Привести основные правила построения сетевой модели
Пояснить порядок расчета сетевой модели на графе
Термины и понятия для запоминания
Путь в сетевой модели, критический путь
Ранний и поздний срок свершения события
Раннее и позднее окончание работы
Исходное и завершающее события
Раннее и позднее начало работы
Резерв времени свершения по событию
1. Иванцов В.М. Методология научной и инженерной деятельности: Учебное пособие / Гос. образоват. учреждение «ГУЦМиЗ». – Красноярск, 2005.
2. Горохов В.Г. Знать, чтобы делать: История инженерной профессии и ее роль в современной культуре. — М.: Знание, 1987.
3. Дьюи Д. Психология и педагогика мышления. Пер. с англ. Н.М. Никольской. – М.: Совершенство, 1997.
4. Пойа Д. Как решать задачу. Пер. с англ. — М.: Учпедгиз, 1959.
5. Халперн Д. Психология критического мышления – СПб.: «Питер», 2000.
6. Альтшуллер Г.С. Найти идею: Введение в теорию решения изобретательских задач. — Новосибирск, Наука, 1986.
7. Попов В.Л. Проектирование строительства подземных сооружений: Учебник для вузов. -2-е изд., перераб. и доп. — М.: Недра, 1989.
8. Быков В.П. Методическое обеспечение САПР в машиностроении. — Л.: Машиностроение. Ленинград. Отделение, 1989.
9. Половинкин А.И. Основы инженерного творчества. — М.: Наука, 1983.
10. Шенк Х. Теория инженерного эксперимента. — М.: Металлургия, 1986.
11. Ганс Селье. От мечты к открытию: Как стать ученым. — М., 1987.
12. Кови Стивен Р. Семь навыков высокоэффективных людей. Возврат к Этике Характера/ Пер. с англ. – М.: АСТ, 1998. – 2-е изд. («Познай себя»).
13. Грачев Н.Н. Психология инженерного труда: Учеб. Пособие. – М. Высш. шк., 1998.
14. Даль В.И. Толковый словарь живого великорусского языка: в 4 тт. – СПб. 1996.
Тема 1.Методология и наш характер: истоки личной эффективности……….
Тема 2.Развитие методологических навыков критического мышления………………
Тема 3.Формирование методологической подготовки и сопровождения
Тема 4.Освоение метода анализа размерностей
с организацией правдоподобных рассуждений «от конца к началу»………….
Тема 5.Разработка методики экспериментального исследования
Тема 6.Составление и расчет сетевой модели организации горных работ……………
Задачи сетевого планирования
На этой странице вы найдете решенные типовые задания из контрольных по сетевому планированию — разделу экономико-математических методов и моделей.
В рамках изучения сетевого анализа студенты обычно учатся: строить график сети по табличному или словесному описанию проекта (и наоборот), находить ранние и поздние сроки начала и окончания работ, резервы, критический путь и минимальное времеия завершения проекта. Более сложные задания подразумевают различные варианты корректировки и оптимизации сетевого графика (с увеличением времени и уменьшением затрат, или наоборот, с уменьшением времени и увеличением расходов), задачи распределения ресурсов. Изучаются различные графические способы отображения как сетевого графика (см. задачи ниже), так и других диаграмм для проекта (диаграмма Ганта, линейный график).
Примеры решений задач по сетевому планированию онлайн
Задача 1. Для заданной сетевой модели некоторого комплекса работ определить время и критический путь.
Задача 2. Издатель имеет контракт с автором на издание его книги. Ниже представлена последовательность (упрощенная) процессов, приводящая к реализации проекта издания книги. Необходимо разработать сеть для этого проекта.
Задача 3. 1. По заданному перечню работ, построить сетевой график.
2. Определить продолжительности полных путей графика.
3. Определить и выделить критический путь.
4. Определить резерв времени каждого пути.
5. Определить коэффициенты напряженности пути.
6. Определить ранние и поздние сроки начала и окончания работы.
7. Определить полный резерв времени каждой работы.
Задача 4. Рассчитать параметры сетевого графика (см. таблицу работ в файле).
Задача 5. На сетевом графике найти ранние и поздние сроки наступления событий, определить критический путь и резервы времени каждого события.
Задача 6. Построить сетевой график. Решить задачу оптимального распределения ресурсов по работам при постоянных интенсивностях. Наличие ресурса R=10. Работы не допускают перерыва в их выполнении.
Задача 7. По данным варианта требуется:
1) построить сетевую модель;
2) определить критические пути модели;
3) провести максимально возможное уменьшение сроков выполнения проекта при минимально возможных дополнительных затратах