Расчет сетевых моделей графическим методом

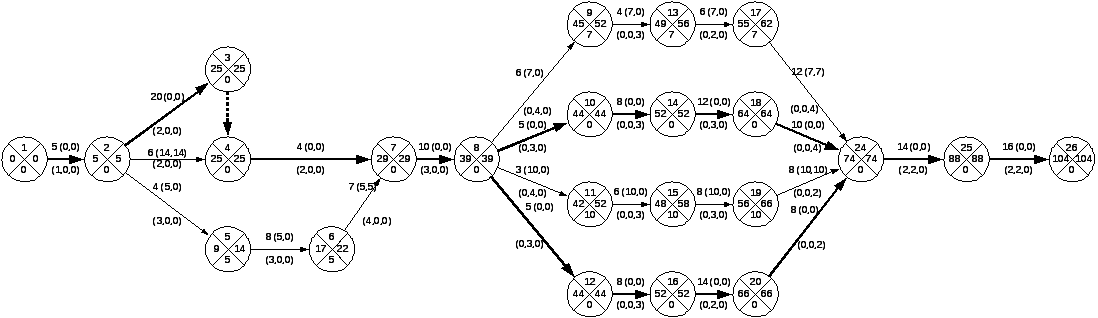
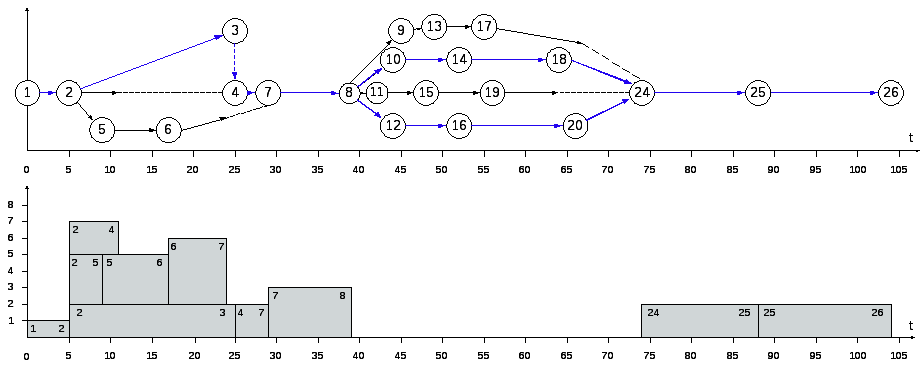
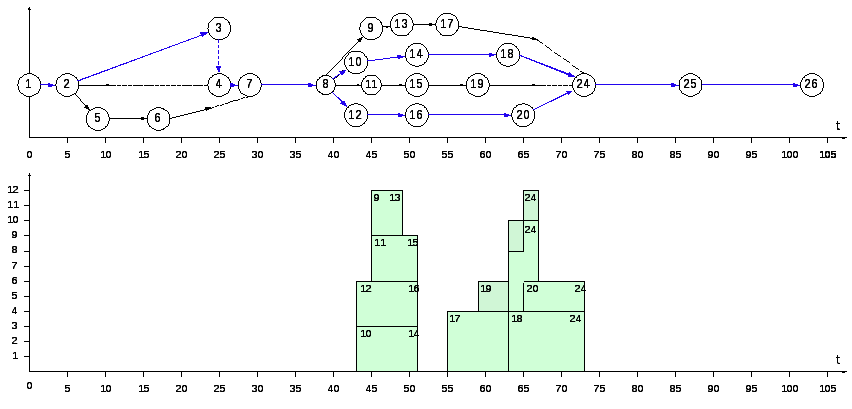
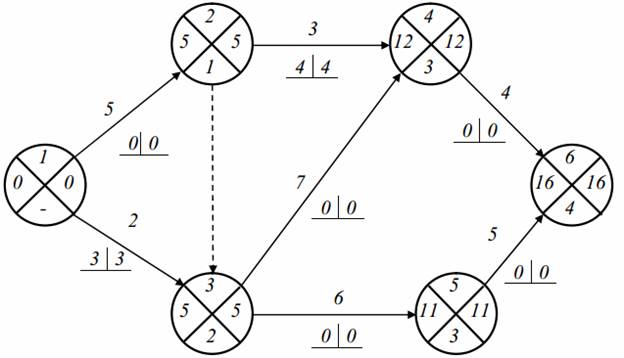
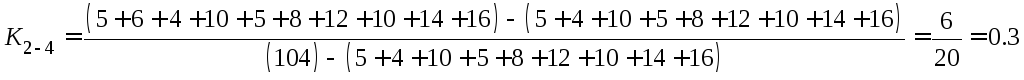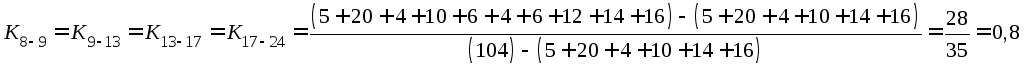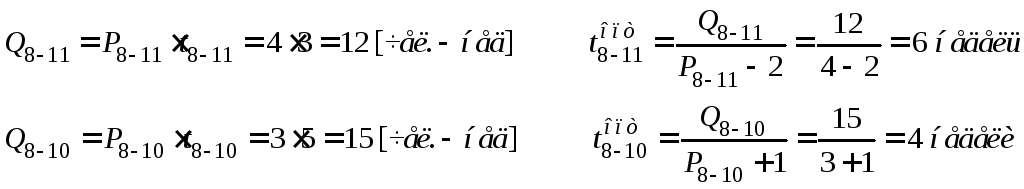Результаты расчета сетевой модели графическим методом

Для больших сетевых моделей целесообразно использовать табличный метод расчета, который позволяет определить параметры сети непосредственно в таблице по определенным правилам. Для сети, изображенной на рис.4, расчет параметров приведен в таблице З.

Расчет параметров сетевой модели табличным методом

Кол-во предшествующих работ работе i,j

Кол-во последующих работ за работой i,j

Правила для заполнения таблицы.

1) Графа 1 заполняется на основе сетевой модели или перечня работ, расположенных в порядке их выполнения.

2) Графа 2 (количество предшествующих работ работе i,j) заполняется следующим образом:

а) для работ, выходящих из исходного события количество предшествующих работ равно 0;

б) для остальных работ количество предшествующих работ определяется по числу работ, имеющих в коде второй цифрой ту, с которой начинается данная работа.

Для работ (0,1), (0,2), (0,3) количество предшествующих работ равно 0.

Для работы (1,4) в графе 1 суммируем количество работ код, которых оканчивается на 1. Это работа (0,1), следовательно, работе (1,4) предшествует одна работа.

Для работы (2,3) в графе 1 суммируем количество работ код, которых оканчивается на 2. Это работа (0,2), следовательно, работе (2,3) предшествует одна работа.

Для работы (2,4) в графе 1 суммируем количество работ код, которых оканчивается на 2. Это работа (0,2), следовательно, работе (2,4) предшествует одна работа.

Для работы (3,4) в графе 1 суммируем количество работ код, которых оканчивается на 3. Это работы (0,3), (2,3), следовательно, работе (3,4) предшествует две работы.

3) Графа 3 (количество последующих работ за работой i,j) определяется по числу работ, имеющих в коде первой цифрой ту, которой заканчивается данная работа (j), если работ начинающихся цифрой j нет, то число последующих работ за работой i,j равно 0.

Для работы (0,1) в графе 1 суммируем количество работ код, которых начинается на цифру 1 . Это работа (1,4), следовательно, за работой (0,1) следует одна работа.

Для работы (0,2) в графе 1 суммируем количество работ код, которых начинается на цифру 2 . Это работы (2,3), (2,4), следовательно, за работой (0,2) следуют две работы.

Для работы (0,3) в графе 1 суммируем количество работ код, которых начинается на цифру 3. Это работа (3,4), следовательно, за работой (0,3) следует одна работа.

Для работы (1,4) в графе 1 нет работ, начинающихся с цифры 4, следовательно количества последующих работ за работой (1,4) нет.

Для работы (2,3) в графе 1 суммируем количество работ код, которых начинается на цифру 3. Это работа (3,4), следовательно, за работой (2,3) следует одна работа.

Для работы (2,4) в графе 1 нет работ, начинающихся с цифры 4, следовательно количества последующих работ за работой (2,4) нет.

Для работы (3,4) в графе 1 нет работ, начинающихся с цифры 4, следовательно количества последующих работ за работой (3,4) нет.

4) Графа 4 заполняется на основе сетевой модели или перечня работ с временными оценками.

5) Графы 5 и 6 заполняются вместе.

Графа 5 (раннее начало работы) определяется путем выбора максимального из сроков раннего окончания предшествующих работ (графа 6). Раннее начало работ, выходящих из исходного события, равно 0 (Трн₀₁ = 0, Трн₀₂ = 0, Трн₀₃ = 0).

Раннее окончание работа (графа 6) определяется суммой раннего срока начала работы (графа 4) и продолжительностью данной работы (графа 3)

6) Графа 8 (позднее окончание работы) заполняется снизу вверх. Для этого полученное максимальное значение в графе 6 заносится в графу 8 для соответствующей работы.

Чтобы определить значение позднего окончания работы для остальных работ необходимо:

а) определить количество последующих работ за рассматриваемой работой (если последующих работ нет, то позднее окончание данной работы принимается равным максимальному значению из графы 6);

б) для последующих работ из графы 8 вычесть графу 4 и выбрать минимальное значение;

в) минимальное значение записать в графу 8 для рассматриваемой работы.

Для рассматриваемого примера максимальное значение в графе 6 равно 14 для работы (3,4). Это число записываем в графу 8 для соответствующей работы.

Для работы (2,4) последующих работ нет, поэтому позднее окончание работы (2,4) равно максимальному значению Тпо₂₄ = 14.

За работой (2,3) следует одна работа (3,4), поэтому Тпо₂₃ = Тпо₃₄ – t₃₄ = 14 – 8 = 6.

Для работы (1,4) последующих работ нет, поэтому позднее окончание работы (1,4) равно максимальному значению Тпо₁₄= 14.

За работой (0,3) следует одна работа (3,4), поэтому Тпо₀₃ = Тпо₃₄ – t₃₄ = 14 – 8 = 6.

За работой (0,2) следуют две работы (2,3) и (2,4), поэтому для определения позднего срока окончания работы (0,2) выбирается минимальное значение из двух величин

За работой (0,1) следует одна работа (1,4), поэтому Тпо₀₁ = Тпо₁₄ – t₁₄ = 14 – 1 = 13

7) Графа 7 (позднее начало работы) находится вычитанием из данных графы 8 данных графы 4 для соответствующих работ.

8) Графа 9 (полный резерв времени работы) определяется как разность между данными графы 8 и графы 6 для соответствующих работ.

9) Графа 11 (резерв времени j-го события) определяется следующим образом. В графе 8 отыскивается позднее окончание работы, заканчивающееся событием j. В графе 5 отыскивается раннее начало работы, начинающееся событием j. Разность этих, величин есть искомый резерв времени события j. Если работ начинающихся событием j нет (графа 5), то резерв времени события j равен 0.

Для работы (0,1) в графе 8 находим позднее окончание работы (0,1), равное 13. В графе 5 находим раннее начало работы, начинающееся событием 1 (работа (1,4)), равное 1. Разность 13 – 1 = 12 есть искомая величина, которая вносится в графу 10 для события 1.

Для работы (0,2) в графе 8 находим позднее окончание работы (0,2) равное 3. В графе 5 находим раннее начало работы, начинающееся событием 2 (работы (2,3), (2,4)), равное 3. Разность 3 – 3 = 0 есть искомая величина, которая вносится в графу 10 для события 2.

Для работы (0,3) в графе 8 находим позднее окончание работы (0,3) равное 6. В графе 5 находим раннее начало работы, начинающееся событием 3 (работа (3,4)) равное 6. Разность 6 – 6 = 0 есть искомая величина, которая вносится в графу 10 для события 3.

Для работ (1,4), (2,4), (3,4) последующих работ начинающихся событием 4 нет, следовательно, резерв времени события 4 равен 0.

10) Графа 10 (свободный резерв времени работы i,j) определяется вычитанием из значений графы 9 значений графы 11 для соответствующей работы.

11) Определяются работы критического пути, код которых заносится в графу 12.

На критическом пути лежат работы, у которых полный резерв времени равен 0 (графа 9). Это работы (0,2), (2,3), (3,4).

Источник

Графический метод расчета параметров сетевого графика

Рассчитать параметры сетевой модели графическим (секторным) методом можно через калькулятор.

Помимо него существуют следующие способы расчета: табличный метод, метод потенциалов.

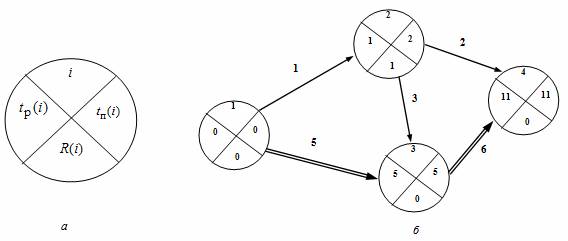
Пример . Определим параметры для событий и критический путь на графике. На практике получил широкое распространение четырехсекторный способ расчета ранних и поздних сроков свершения событий. При этом способе кружок сетевого графика, обозначающий событие, делится на четыре сектора (рис. 2, а). В верхнем ставится номер события i, в левом – наиболее раннее из возможных время свершения события t_p(i), в правом – наиболее позднее из допустимых время свершения события t_п(i), в нижнем – резерв времени данного события R(i).

Рисунок 2 — Графический способ расчета параметров: а) обозначения в вершине графика; б) сетевой график.

Раннее время свершения события t_p(i) определяется продолжительностью максимального пути max(t) до (i), предшествующего событию i: t_p(i)=max(t) до (i).
Послойно, переходя от исходного события до конечного, определим t_p(i). Всегда для начального события t_p(1)=0.
Для события 3 (рис., б) – t_p(3)=max=5; для события 4 – t_p(4)=max=11.
Длина критического пути L_кр=11. Послойно, переходя от конечного события до начального, определим t_п(i). Всегда для конечного события t_п(4)=t(L_кр)=11. Позднее время свершения события t_п(i) определяется временем достаточным для выполнения работ, следующих за этим событием, т.е. зная продолжительность максимального из последующих за событием i путей max(t) после (i) и продолжительность критического пути t(L_кр), можно найти t_п(i)= t(L_кр)-max(t) после (i).
Для события 2 – t_п(3)=11-max=2.
Для критического пути время раннего свершения события t_p(i) равно времени позднего свершения этого события t_п(i), т.е. t_p(i)= t_п(i). Зная ранние и поздние сроки свершения событий сетевого графика, легко выявить резерв времени каждого из них R(i)= t_п(i)- t_p(i).
Резерв времени события показывает максимально допустимое время, на которое можно отодвинуть момент его свершения, не вызывая увеличения критического пути. События критического пути резерва времени не имеют.
Связь параметров сетевого графика для событий и работ показана в таблице.

Таблица — Расчет параметров работ

Время	Начало i → j Окончание
Раннее	tрн(ij)= tp(i)	tро(ij)= tp(i)+tij
Позднее	tпн(ij)= tп(j)-tij	tпо(ij)= tп(j)

Резерв времени для работы R(ij) определяется по формуле: R(ij)= t_п(j)- t_р(i)-t_ij.

Источник

Этап 3. Расчет параметров сетевой модели графическим методом; определение критического пути и его продолжительности.

• Ранний срок свершения события ;
• Поздний срок свершения события ;
• Резерв времени события ;
• Полный резерв времени события ;
• Свободный резерв времени события .

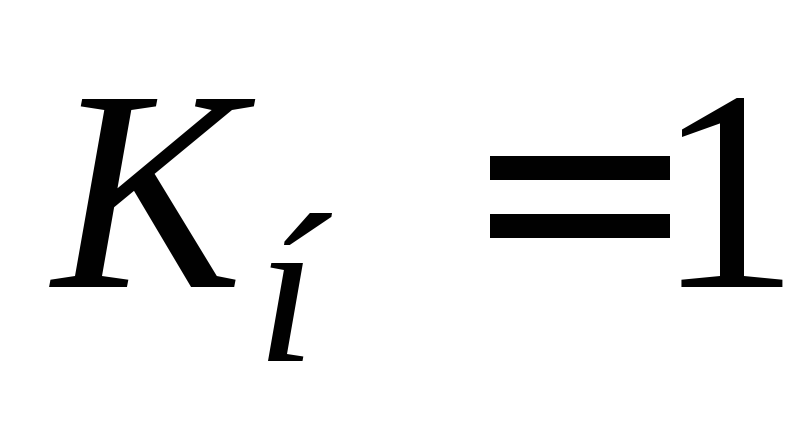
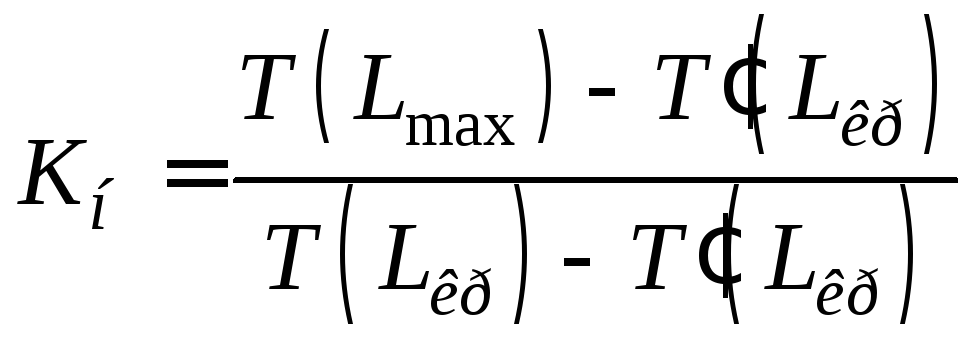
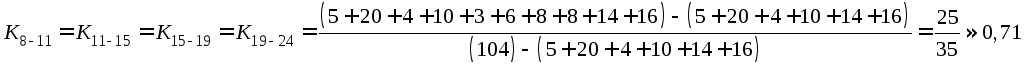
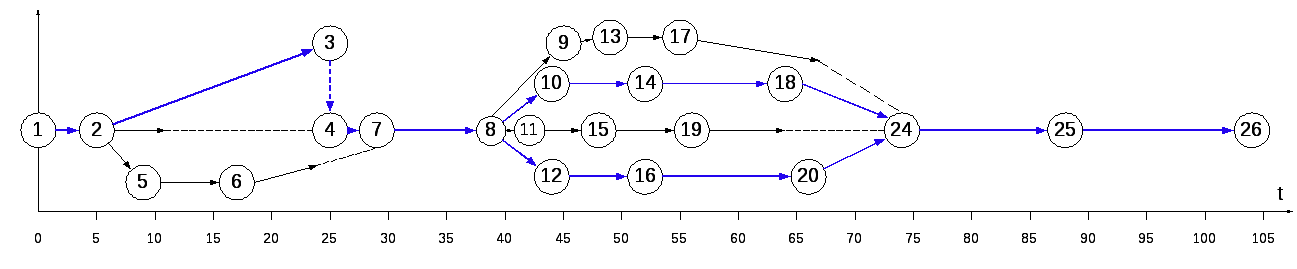
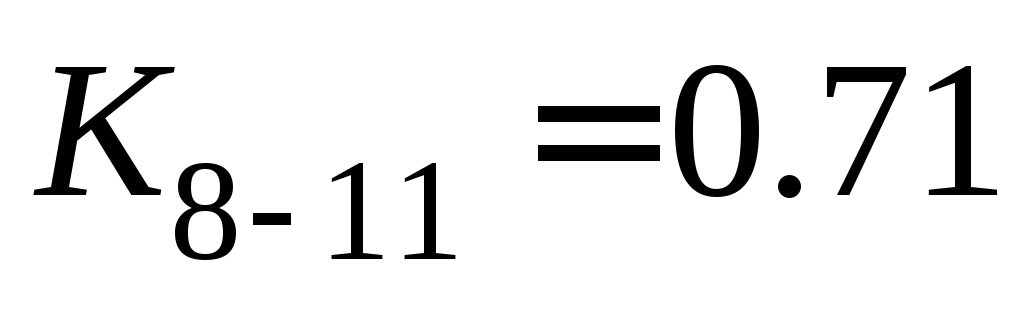
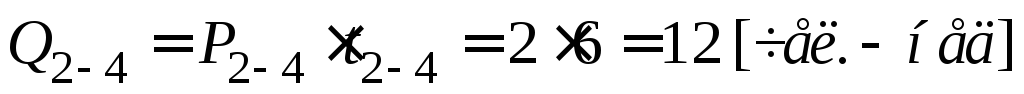
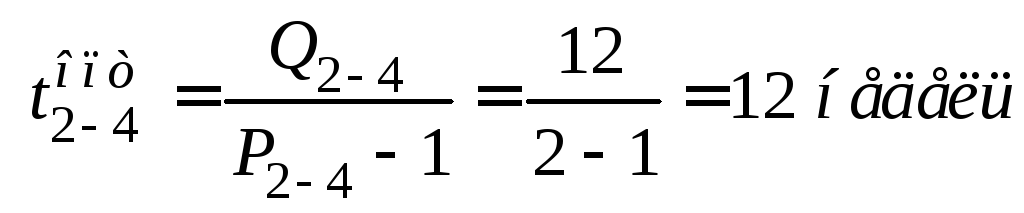
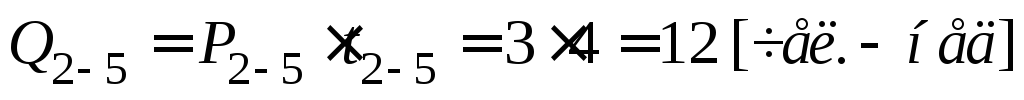
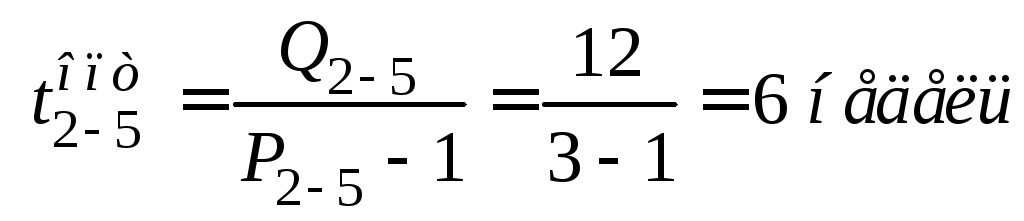
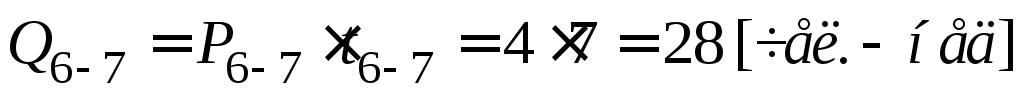
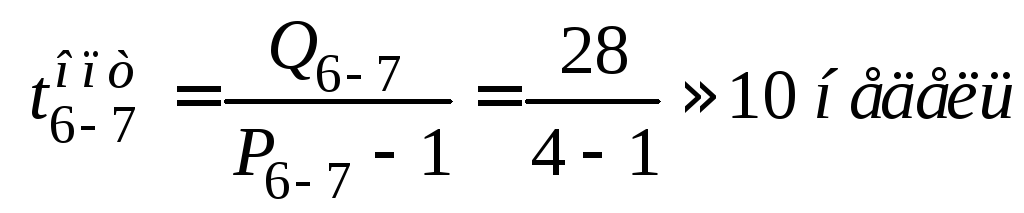
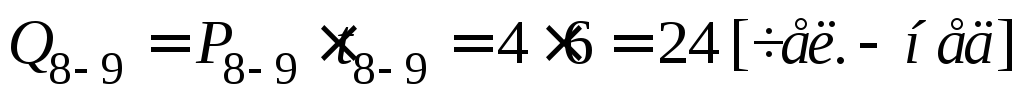
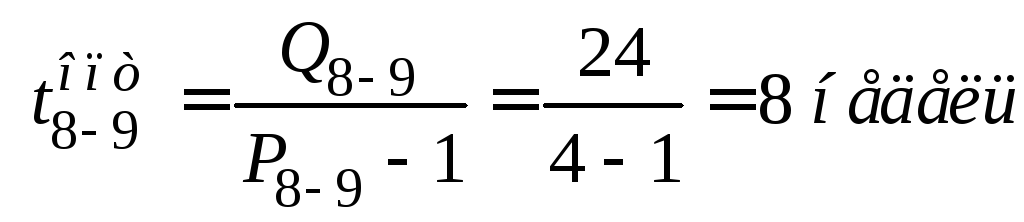
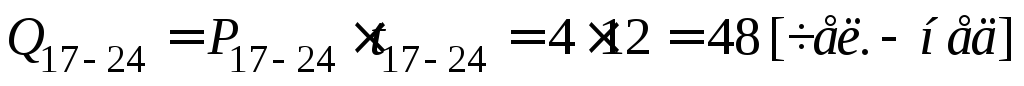
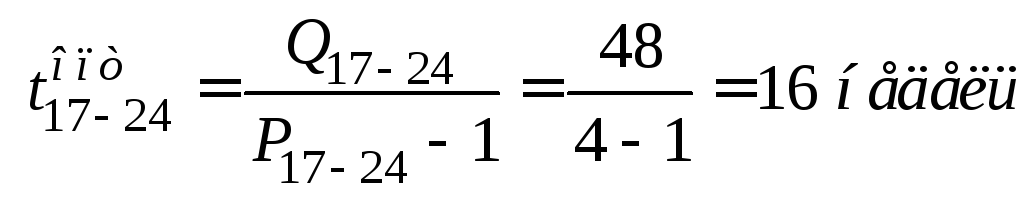
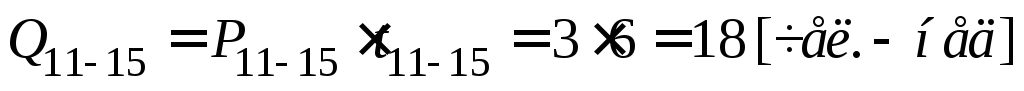
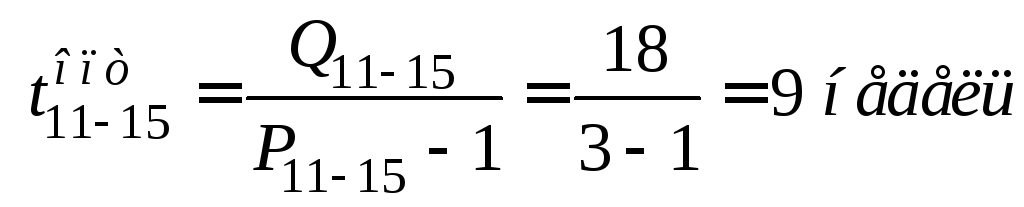
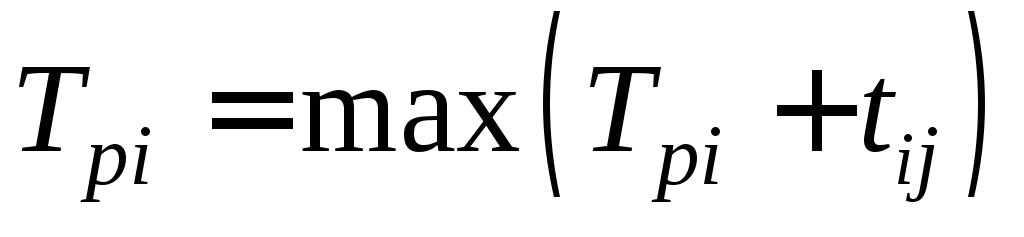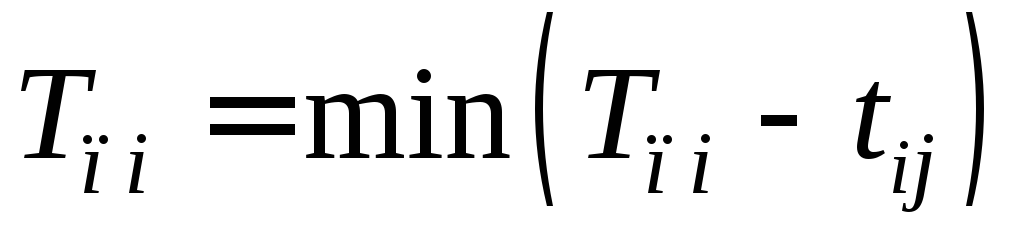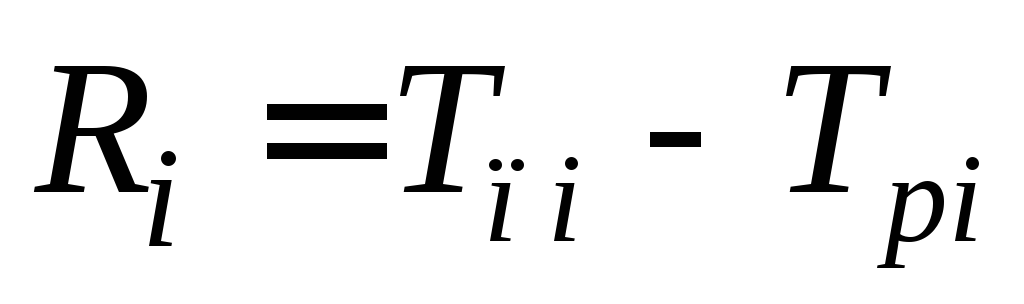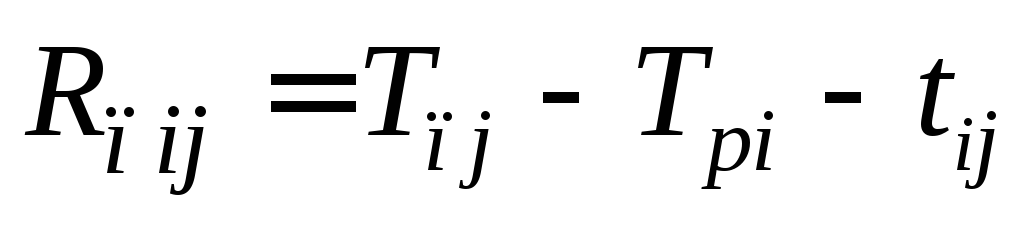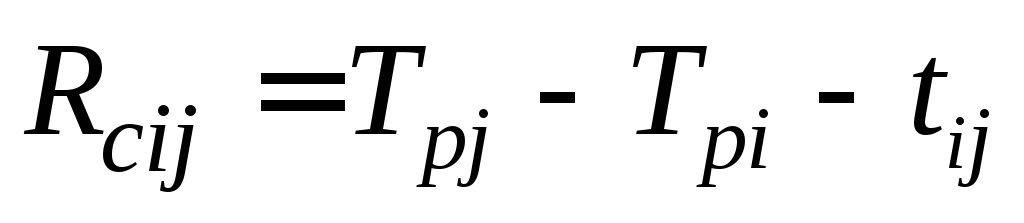Рис 3. Результат расчета параметров сетевой модели графическим методом. Критический путь: 1-2-3-4-7-8-10-14-18-24-25-26, 1-2-3-4-7-8-12-16-20-24-25-26. Длина критического пути T(Lкр) = 104. Этап 4. Расчет коэффициентов напряженности работ. Коэффициенты напряженности работ, находящихся на критическом пути: Коэффициенты напряженности для остальных участков сетевого графика вычисляются по формуле . Работы 8-9, 9-13, 13-17, 17-24 являются работами подкритического пути. Этап 5. Построение сетевой модели выполнения комплекса работ в шкале времени.Рис 4. Сетевой график в шкале времени. Этап 6. Построение графиков загрузки исполнителей по каждой профессии (отдельно) в шкале времени (на одном листе с сетевым графиком).Рис 5. Сетевой график в шкале времени и график загрузки ведущих инженеров. Рис 6. Сетевой график в шкале времени и график загрузки старших инженеров. Рис 7. Сетевой график в шкале времени и график загрузки инженеров. Этап 7. Оптимизация сетевой модели по времени с помощью сокращения продолжительности критического пути Т_кр, т.е. длительности цикла выполнения комплекса работ, на одну — две единицы времени. Для оптимизации выбрана работа 8-11 с коэффициентом напряженности . Переведем одного старшего инженера с работы 8-11 на работу критического пути 8-10 и одного старшего инженера на работу критического пути 8-12. Таким образом, продолжительность критического пути сократилась на 1 неделю и составляет теперь 103 недели. Этап 8. Отображение результатов оптимизации на сетевом графике в шкале времени.Рис 8. Сетевой график выполнения комплекса работ в шкале времени после оптимизации по времени. Этап 9. Построение графика загрузки исполнителей по каждой профессии (отдельно) в шкале времени после оптимизации (на одном листе с сетевым графиком).Рис 9. Сетевой график выполнения комплекса работ в шкале времени и график загрузки ведущих инженеров после оптимизации по времени. Рис 10. Сетевой график выполнения комплекса работ в шкале времени и график загрузки старших инженеров после оптимизации по времени. Рис 11. Сетевой график выполнения комплекса работ в шкале времени и график загрузки инженеров после оптимизации по времени. Этап 10. Оптимизация сетевой модели по численности исполнителей и их загрузке; отображение результатов оптимизации на сетевом графике в шкале времени. 1) Численность ведущих инженеров будет оптимизирована за счет работ 2-4, 2-5, 6-7, так как наибольшая нагрузка ведущих инженеров наблюдается во время выполнения данных работ. Объём работы 2-4: Сократим численность до 1 человека. Объём работы 2-5: Сократим численность до 2 человек. Объём работы 6-7: Сократим численность до 3 человек. 2) Загрузка старших инженеров максимальна на участке 39-43. Резерв времени позволяет провести оптимизацию работы 8-9. Объём работы 8-9: Сократим численность до 3 человек. 3) Загрузка инженеров максимальна на участках 45-49 и 65-67. Резерв времени позволяет провести оптимизацию на работах 17-24 и 11-15. Объём работы 17-24: Сократим численность до 3 человек. Объём работы 11-15: Сократим численность до 2 человек. В результате оптимизации сетевой модели по численности количество ведущих инженеров сократилось на 3 человек, количество старших инженеров – на 1 человека, количество инженеров – на 2 человек. К тому же, появился новый критический путь.

Источник