Методы расчета временных параметров и критического пути сетевой модели проекта
Если размеры сетевого графика невелики, то его временные параметры и критический путь могут быть найдены путем непосредственного рассмотрения графика вершина за вершиной, работа за работой. Но, естественно, по мере увеличения масштабов модели вероятность появления ошибки в расчетах будет возрастать в геометрической прогрессии. Поэтому, даже при небольших размерах модели целесообразно воспользоваться одним из наиболее подходящих алгоритмических методов расчета, позволяющих подойти к этой задаче формально.
Самыми распространенными методами расчета временных параметров сетевой модели являются табличный и матричный. Поэтому, даже если исходная информация по сетевой модели представлена в виде сетевого графика или временной диаграммы, приступая к анализу, ее следует привести к табличной либо матричной форме.
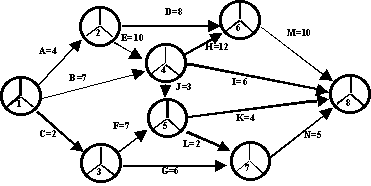
В качестве примера будем рассматривать модель, заданную изначально сетевым графиком, приведенным на рис. 6.
Рисунок 6. Пример сетевого графика для иллюстрации методов расчета временных параметров
Как табличный, так и матричный метод расчета временных параметров сетевой модели основывается на следующих соотношениях, вытекающих из определений временных параметров. Для удобства понимания индекс работы, как правило, состоит из двух букв, например, [ij], первая из которых соответствует индексу начального события работы, а вторая – индексу конечного события работы. С учетом этого замечания:
- Раннее время начала работы [ij] совпадает с ранним временем наступления события [i], т.е. ESTij = EET [i].
- Позднее время окончания работы [ij] совпадает с поздним временем наступления события [j], т.е. LFTij = LET [j].
- Раннее время окончания работы [ij]:
- Позднее время начала работы [ij]: LSTij = LFTij – tij.
- Раннее время наступления события [j] совпадает с самым поздним (максимальным) ранним временем окончания из всех тех работ, для которых данное событие является конечным, т.е. EET[j] = max , где [rj], [nj], . [mj] – индексы работ, для которых событие [j] является конечным.
- Позднее время наступления события [j] совпадает с самым ранним (минимальным) поздним временем начала из всех тех работ, для которых данное событие является начальным, т.е. LET[j] = min < LSTjr, LSTjn, . LSTjm>, где [jr], [jn], . [jm] – индексы работ, для которых событие [j] является начальным.
- Для исходного и заключительного события сетевой модели справедливо: EET[s] = LET[s]
- Но если для исходного события принимается, как правило, момент времени, равный 0, то для заключительного события он появляется в результате расчетов и по нему можно судить о продолжительности критического пути. Итак, для заключительного события справедливо: EET[f] = LET[f] = TK, где TK – продолжительность критического пути.
- Полный резерв времени выполнения работы [ij]: TFij = LЕT[j] – EET[i] – tij.
- Свободный резерв времени выполнения работы [ij]: FFij = EЕT[j] – EET[i] – tij.
- Независимый резерв времени выполнения работы [i]: IFi = EЕT[j] – LET[i] – tij.
Расчет временных параметров сетевой модели проектируемого производственного процесса
После определения ожидаемой продолжительности работ приступают к расчету временных параметров сетевого графика. К параметрам сетевого графика относятся:
- продолжительность критического пути – t(Lкр);
- ожидаемая продолжительность работы — tожij (i, j — соответственно номера начального и конечного события для данной работы; i — предшествующее событие; j — последующее);
- раннее начало работы — самое раннее время, когда работа может
быть начата – tрнij;
- раннее окончание работы — время завершения работы, если она начата в ранний срок — tроij;
- позднее начало работы — время, не вызывающее увеличения срока реализации производственного процесса — tпнij;
- позднее окончание работы — время, при котором общая длительность производственного цикла не изменяется — tпоij;
- ранний срок наступления события – tр;
- поздний срок наступления события – tп;
- резерв времени события j – Rj;
- полный резерв времени работы ij — Rпij;
- свободный резерв времени работы ij — Rсвij.
Основным параметром сетевого графика является критический путь. Критический путь— это наиболее протяженная во времени цепочка работ, идущих от исходного к завершающему событию. Критическими также называют все события, лежащие на этом пути. Изменение продолжительности любой критической работы соответственно изменяет (сокращает или удлиняет) срок наступления завершающего события, т.е. время достижения конечной цели производственного процесса. Другим важнейшим параметром сетевой модели является резерв временисвершения событий. Резерв времени— это такой промежуток времени, на который может быть отсрочено наступление события без нарушения сроков завершения процесса в целом. Резерв времени события определяется как разность между поздним и ранним сроками наступления события. Полный резерв времени работы(Rпij) — показывает на сколько можно увеличить время выполнения данной работы при условии, что срок выполнения комплекса работ не изменится. Свободным резервом можно пользоваться для предотвращения случайностей, которые могут возникнуть в ходе производственного процесса. Если планировать выполнение работ по ранним срокам их начала и окончания, то всегда будет возможность перейти на позднее начало и окончание работ. Работы, лежащие на критическом пути, также как и критические события, резервов времени не имеют. Для расчета параметров сетевой модели (сетевого графика) существуют несколько методов, основными из которых являются: 1. Графический метод — вычисление параметров непосредственно на сетевом графике.
- Табличный метод — заключается в последовательном заполнении таблицы параметров сети по определенным правилам.
Вычисления параметров графическим методом (непосредственно на сетевом графике) применяется в тех случаях, когда число событий невелико (до 15-20 событий). Для этого каждый кружок, изображающий событие, разделяется на четыре сектора. Верхний сектор отводится для номера события, левый — для указания вычисляемых ранних сроков наступления событий, правый — для указания поздних сроков наступления событий, нижний сектор — для указания резервов времени событий. В дальнейшем соблюдается следующий порядок расчета основных параметров. 1. Ранний и поздний сроки свершения исходного события принимаются равными нулю: 2. Ранний срок свершения любого конечного события (tрj) определяется максимальной суммой раннего срока свершения начального события работы ij и продолжительности этой работы: 3. Поздний срок завершающего события всегда равен его раннему сроку. 4.Поздний срок предшествующего i-го события определяется минимальной разностью между поздним сроком свершения конечного события работы ij и продолжительностью этой работы: 5. Определяют резервы времени событий (Ri): 6. На сетевую модель наносится критический путь, определяемый как последовательность работ, соединяющих события с нулевыми резервами времени.
| № п/п | Наимено вание работы | Код работы | Оценка продолжитель ности | Ожидаемая продолжительность работы 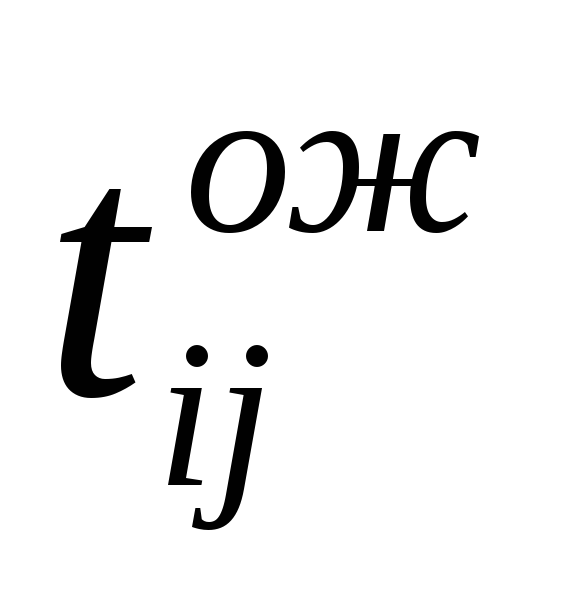 |  с учетом Кп с учетом Кп | |
| Максим | Миним | |||||
| 1 | 1-2 | 8 | 5 | 6,2 | 7 | |
| 2 | 1-3 | 10 | 6 | 7,6 | 8 | |
| 3 | 1-5 | 7 | 3 | 4,6 | 5 | |
| 4 | 2-4 | 11 | 7 | 8,6 | 9 | |
| 5 | 3-4 | 8 | 4 | 5,6 | 6 | |
| 6 | 3-6 | 7 | 4 | 5,2 | 6 | |
| 7 | 4-8 | 8 | 5 | 6,2 | 7 | |
| 8 | 5-7 | 8 | 5 | 6,2 | 7 | |
| 9 | 6-8 | 7 | 4 | 5,2 | 6 | |
| 10 | 7-8 | 14 | 11 | 12,2 | 13 | |
| 11 | 8-9 | 26 | 15 | 19,4 | 20 | |
При больших размерах сетевой модели целесообразно использовать табличный метод расчета, который позволяет определить ее параметры непосредственно в таблице. Временные параметры сетевой модели производственного процесса
| Код работы | Ожидаемая продолжительность работы  | Ранний срок свершения события | Поздний срок свершения события | Резерв Rj | ||
| tрi раннее начало | tрj раннее окончание | tпi позднее начало | tпj позднее окончание | |||
| 1-2 | 7 | |||||
| 1-3 | 8 | |||||
| 1-5 | 5 | |||||
| 2-4 | 9 | |||||
| 3-4 | 6 | |||||
| 3-6 | 6 | |||||
| 4-8 | 7 | |||||
| 5-7 | 7 | |||||
| 6-8 | 6 | |||||
| 7-8 | 13 | |||||
| 8-9 | 20 | |||||
Методы расчета временных параметров и критического пути сетевой модели проекта
Если размеры сетевого графика невелики, то его временные параметры и критический путь могут быть найдены путем непосредственного рассмотрения графика вершина за вершиной, работа за работой. Но, естественно, по мере увеличения масштабов модели вероятность появления ошибки в расчетах будет возрастать в геометрической прогрессии. Поэтому, даже при небольших размерах модели целесообразно воспользоваться одним из наиболее подходящих алгоритмических методов расчета, позволяющих подойти к этой задаче формально.
Самыми распространенными методами расчета временных параметров сетевой модели являются табличный и матричный. Поэтому, даже если исходная информация по сетевой модели представлена в виде сетевого графика или временной диаграммы, приступая к анализу, ее следует привести к табличной либо матричной форме.
В качестве примера будем рассматривать модель, заданную изначально сетевым графиком, приведенным на рис. 6.
Рисунок 6. Пример сетевого графика для иллюстрации методов расчета временных параметров
Как табличный, так и матричный метод расчета временных параметров сетевой модели основывается на следующих соотношениях, вытекающих из определений временных параметров. Для удобства понимания индекс работы, как правило, состоит из двух букв, например, [ij], первая из которых соответствует индексу начального события работы, а вторая – индексу конечного события работы. С учетом этого замечания:
- Раннее время начала работы [ij] совпадает с ранним временем наступления события [i], т.е. ESTij = EET [i].
- Позднее время окончания работы [ij] совпадает с поздним временем наступления события [j], т.е. LFTij = LET [j].
- Раннее время окончания работы [ij]: EFTij = ESTij + tij.
- Позднее время начала работы [ij]: LSTij = LFTij – tij.
- Раннее время наступления события [j] совпадает с самым поздним (максимальным) ранним временем окончания из всех тех работ, для которых данное событие является конечным, т.е. EET[j] = max , где [rj], [nj], . [mj] – индексы работ, для которых событие [j] является конечным.
- Позднее время наступления события [j] совпадает с самым ранним (минимальным) поздним временем начала из всех тех работ, для которых данное событие является начальным, т.е. LET[j] = min < LSTjr, LSTjn, . LSTjm>, где [jr], [jn], . [jm] – индексы работ, для которых событие [j] является начальным.
- Для исходного и заключительного события сетевой модели справедливо: EET[s] = LET[s]
- Но если для исходного события принимается, как правило, момент времени, равный 0, то для заключительного события он появляется в результате расчетов и по нему можно судить о продолжительности критического пути. Итак, для заключительного события справедливо: EET[f] = LET[f] = TK, где TK – продолжительность критического пути.
- Полный резерв времени выполнения работы [ij]: TFij = LЕT[j] – EET[i] – tij.
- Свободный резерв времени выполнения работы [ij]: FFij = EЕT[j] – EET[i] – tij.
- Независимый резерв времени выполнения работы [i]: IFi = EЕT[j] – LET[i] – tij.