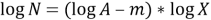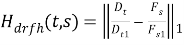Анализ метода стратегии оптимизации распределения информационно-вычислительных ресурсов в кластерах
Смирнов, М. В. Анализ метода стратегии оптимизации распределения информационно-вычислительных ресурсов в кластерах / М. В. Смирнов, К. П. Климченко, С. О. Потапов. — Текст : непосредственный // Молодой ученый. — 2022. — № 22 (417). — С. 28-32. — URL: https://moluch.ru/archive/417/92434/ (дата обращения: 13.07.2023).
В статье рассматривается проблема хранения и обработки растущих информационных потоков, решаемая в предлагаемой перспективе с помощью оптимизации существующих стратегий распределения вычислительных ресурсов.
Ключевые слова: распределение вычислительных ресурсов, вычислительные кластеры, задачи оптимизации.
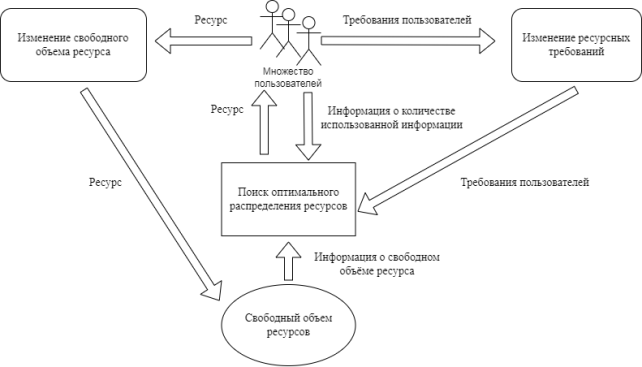
Количество информации в интернете постоянно растёт, примерно по 50 % в год, следовательно, и информации, которую необходимо хранить, обрабатывать и передавать, тоже становится больше. На момент 2018 года весь объём хранимых данных в интернете насчитывал 33 зеттабайта, сейчас же объём данных занимает около 70 зеттабайт, а на 2025 по расчётам различных учёных, предположительный объём данных будет составлять 175 зеттабайт. Такое количество информации способны обрабатывать только кластерные системы. Кластер подразумевает под собой два или более компьютеров (узлов, объединённых при помощи сетевых технологий на базе шинной архитектуры или коммутатора и являющиеся для пользователя единым информационно-вычислительным ресурсом. Из-за большого объёма количество информации просто кластера недостаточно, и кластеры объединяют в целые кластерные системы [5]. Кластеры выполняют задачи не только обработки информации, но и хранения, а также выполняют функции по поиску информации. Из-за большого спектра выполняемых задач кластерными системами, главной проблемой становится задача по управлению распределением информационно-вычислительных ресурсов в РСОИ [3]. РСОИ — это распределённые системы обработки информации и их главной задачей становится выбор наиболее устойчивой, эффективной и надёжной стратегии распределения информационно-вычислительных ресурсов для реализации разделяемого коллективного режима доступа к ресурсам. В условиях постоянного роста количества информации и запросов пользователей [4] на первый план выходит потребность в оптимальном использовании ограниченных ресурсов РСОИ. Задача оптимального распределения ресурсов заключается в выборе наилучшего варианта использования ограниченного ресурса таким образом, чтобы потребности пользователей были удовлетворены в полном объеме, а количество простаивающего ресурса стремилось к нулю. Следовательно, задачу распределения ресурсов можно свести к нескольким параметрам: свободный объём ресурсов и ресурсные требования пользователей. А в самой задаче нам необходимо учитывать процесс изменения данных параметров и решать задачу оптимального распределения свободных ресурсов [2]. Если представить данную задачу в виде схемы, то она будет выглядеть так (рис. 1).
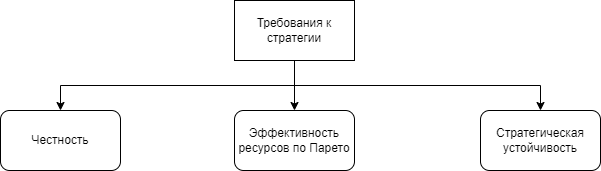
На основе представленной схемы можно понять, что эффективность алгоритма заключается в эффективности планирования распределения ресурсов. Данных методов, способов и стратегий распределения вычислительных ресурсов множество и каждый из них работает по собственному алгоритму. В данной статье рассмотрим основные стратегии. Стратегия распределения информационных и вычислительных ресурсов — это комплекс управленческих решений о типе канала, его структуре и масштабах, а также контроле и управлении структурными элементами канала. Канал распределения –совокупность пользователей, включенных в процесс обмена ресурсами, обеспечивающий доступность для конечных потребителей. Что должна делать стратегия? Ее важнейшая функция — решить, задачу какого из пользователей запустить. У нее есть множество различных вычислений, которые заказали пользователи, и ей надо понять, какую задачу из этих вычислений или операций надо запустить. Также стратегии необходимо понять, чего хотят пользователи. Очевидно, что каждый из пользователей запуская свою задачу на вычисление или обработку информации, желает каких-то гарантий — желает, чтобы его задача завершилась и как можно скорее. Поэтому стратегиям оптимального распределения ресурсов выдвигают ряд требований, основанных на концепции стратегического управления Венсила-Лагранжа, основные из которых представлены на схеме ниже (рис. 2).
Рис. 2. Требования к стратегиям
Требование «Честность» минимально исполняется в стратегиях, основанных на приоритете времени обращения. В то время, как ресурсы занимаются пользователем, например, допустившим ошибку, которая увеличила время вычислений, другие пользователи находятся в режиме ожидания. «Эффективность ресурсов по Парето». В экономике по «закону Парето [1]» можно вычислить зависимость между величиной дохода и количеством получающих его лиц по формуле (1):
Где N — число людей в обществе с доходами, не меньше, чем X; A и m — параметры данного распределения. Но для данного случая этот параметр предполагает использование ресурсов, не допуская их простаивания. Если существует запрос пользователя на исполнение задачи, при существующих свободных ресурсах, то ресурсы должны быть выделены. «Стратегическая устойчивость» формализуется исходя из стратегии, для которой это требование применяется. Пользователь может запросить больше ресурсов, чем того требует задача. Стратегия должна создать максимально невыгодные условия для привлечения избыточного количества ресурсов. Одной из стратегий, удовлетворяющих данным требованиям, является DRF (Dominant Resource Fairness). Она основана на понятии доминантного ресурса, то есть, на ресурсе, наибольшую долю которого потребляет пользователь. Например, для пользователя, которому выделено 1/5 CPU и 1/8 оперативной памяти кластера, то доминантным ресурсом для этого пользователя является CPU. Доминантная доля пользователя — доля потребления пользователем его доминантного ресурса. В данном примере 1/5 CPU является доминантной долей пользователя. Одна из проблем заключается в определении доминантной доли. При использовании одного ресурса берётся количество этого ресурса и делится на суммарный ресурс в кластере. При множестве ресурсов вычисляется доля потребления ресурсов конкретной операции, то есть одно число, просто как долю максимального ресурса в данной операции.
Стратегия DRF соответствует требованию честность, если для любой операции верно, что доля ресурсов, которые она потребила или потребляет при некотором количестве итераций больше либо равна ее весу. «Эффективность по Парето» соблюдается с помощью перебора операций, выбирая ту, у которой отношение веса операции к реальному текущему потреблению ресурсов больше. Сохранение «стратегической устойчивости» также осуществляется стратегией. Если операция запросила больше доминантного ресурса, то это число начнет увеличиваться быстрее, чем раньше. За счет такого сильного увеличения, этого ресурса выделится меньше. Одна из проблем стратегии — возможность сговора. Сговор происходит между пользователями с равным весом операции с помощью ресурса, у которого суммарные требования больше всего. Чем больше суммарные требования, тем большему количеству пользователей необходим этот ресурс. Вторая проблема — отсутствие внутренней иерархии задач. Пользователь хочет иметь возможность внутри выделенного процента кластера распределить ресурсы. Например, внутри выделенных 15 % кластера отдать на одну задачу 30 % ресурсов, а на вторую 70 %, исходя из взглядов пользователя на важность данных задач. Один из способов решения этой проблемы — min satisfaction HierarchyDRF. В данном случае при выборе, какой задаче дать ресурс, рассматривается не только доминантный ресурс всего пула, но и для каждого узла в поддереве тоже посчитывается отношение. То есть, в данном случае, внимание уделяется на отношение и в этом узле, и в его детях. При таком действие алгоритма он предоставляет как минимум обещанную долю ресурсов. Вместо запуска данной задачи на случайном сервере есть возможность выбрать сервер с наименьшим значением данной эвристической функции по формуле (2):
Где t — идентификатор задачи; s — идентификатор сервера; Dt — вектор запроса ресурсов (demand) задачи t; Fs — вектор свободных ресурсов на сервере s; Dt1 и Fs1 — первые компоненты соответствующих векторов; ∥·∥1-норма, т. е. сумма компонент вектора. Недостатком данной эвристики является то, что он влияет на планирование только в тех случаях, когда есть выбор, на каком сервере запустить задачу, что в реальности не всегда возможно из-за высокой нагрузки на кластер. Когда на кластере задача заканчивает своё выполнение и освобождает ресурсы, планировщик должен запустить новые задачи и задействовать освободившиеся ресурсы с минимальной задержкой, чтобы избежать простаивания ресурсов.
Но практика показывает, планировщик, как правило, не имеет широкого выбора серверов, на которых можно запустить задачу, что делает метод менее эффективным.
В данной работе рассмотрена задача оптимального распределения ресурсов на одной из стратегий. Несмотря на соответствие основным требованиям к стратегии, DRF имеет свои недостатки, которые невозможно игнорировать. А конкретно, возможность сговора и отсутствие внутренней иерархии задач. Благодаря внедрению min satisfaction HierarchyDRF эффективность алгоритма выросла на 5–10 %. Несмотря на отсутствие широкого выбора серверов для запуска задач из-за нагрузки на кластер. Тем не менее, в работе остались вопросы, требующие дополнительного исследования. Во-первых, требуется в информационных технологиях в управлении определить необходимые и достаточные условия существования и единственности решения рассмотренной задачи оптимизации по обобщенному критерию. Во-вторых, необходимо исследовать задачу оптимизации для дискретного ресурса. В-третьих, детальнее изучить проблему сговора между пользователями. Несмотря на кажущуюся простоту описания требований, остаётся неизвестным существование стратегии решения.
- Пулькин, И. С. Статистические свойства показателя распределения Парето / И. С. Пулькин, А. В. Татаринцев // Cloud of Science. — 2020. — Т. 7. — № 3. — С. 498–509. — EDN HZAWKC.
- Ворожцов, А. С. Динамическое распределение вычислительных ресурсов центров обработки данных / А. С. Ворожцов, Н. В. Тутова, А. В. Тутов // T-Comm: Телекоммуникации и транспорт. — 2016. — Т. 10. — № 7. — С. 47–51. — EDN WINJQL.
- Козлов, С. В. Оптимальное распределение информационно-вычислительных ресурсов на основе двухуровневого критерия / С. В. Козлов, Ю. П. Остриков, А. Л. Суханов // Управление большими системами: сборник трудов. — 2014. — № 48. — С. 71–84. — EDN THZLJN.
- Болодурина, И. П. Алгоритмы комплексной оптимизации потребления вычислительных ресурсов в облачной системе дистанционного обучения / И. П. Болодурина, Д. И. Парфенов // Вестник Оренбургского государственного университета. — 2013. — № 9(158). — С. 177–184. — EDN RLEABL.
- Метод обработки данных с учетом взаимного расположения информационных блоков в масштабе вычислительного кластера / Е. А. Кулешова, А. Л. Марухленко, В. П. Добрица [и др.] // Вестник Воронежского государственного университета. Серия: Системный анализ и информационные технологии. — 2021. — № 1. — С. 87–97. — DOI 10.17308/sait.2021.1/3373. — EDN RUMDWE.
Основные термины (генерируются автоматически): ресурс, CPU, DRF, задача, пользователь, доминантный ресурс, стратегия, кластер, оптимальное распределение ресурсов, требование.