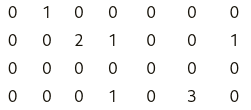Разреженная матрица сетевая модель данных

Разреженные матрицы: как ученые ускорили машинное обучение на GPU

В начале декабря исследователи из OpenAI представили библиотеку инструментов, которая поможет ускорить обучение нейронных сетей на GPU от Nvidia за счет использования разреженных матриц. О том, с какими трудностями сталкиваются разработчики нейронных сетей и в чем основная идея решения от OpenAI, расскажем далее.

Трудности тренировки крупных нейронных сетей на GPU

Графические процессоры (GPU) лучше подходят для машинного обучения, чем центральные процессоры (CPU). Технические особенности помогают GPU выполнять одновременно множество матричных операций, которые используются для обучения нейронных сетей.

Чтобы добиться схожего результата на центральном процессоре, придется выстроить инфраструктуру из нескольких кластеров CPU, что очень дорого. Система Google для тренировки нейросетей на CPU стоила порядка 5 млрд долларов. Сегодня ученые из Стэнфорда построили систему с аналогичной вычислительной мощностью на GPU всего за 33 тыс. долларов.

Однако здесь есть трудности: использовать весь потенциал GPU на ресурсоемких задачах не так просто. Для обработки данные должны храниться в памяти GPU, однако её объем невелик, что затрудняет тренировку крупных моделей. Например, модель VGG-16 требует около 14 ГБ, в то время как объем памяти Nvidia Titan X составляет 12 ГБ. И эту карту Nvidia позиционирует как один из самых мощных GPU для глубокого обучения.

Как верно заметил EvilGenius18 в комментариях, 7 декабря компания Nvidia представила новую карту Titan V на архитектуре Volta. Она обладает вычислительной мощностью 110 TFLOPS на задачах глубокого обучения, что в 9 раз больше, чем у предшественницы.

При этом для эффективной тренировки крупных моделей нейронных сетей используют различные подходы. Один из них — обработка данных на графическом процессоре последовательными партиями, когда CPU выступает временным контейнером. Минус такого подхода — расходование ресурсов на перенос данных.

Возможно одновременное использование нескольких графических процессоров, но количество GPU на одном компьютере ограничено, поэтому требуется высокоскоростное соединение между вычислительными системами. Межкомпьютерный канал связи сказывается на скорости обучения, поскольку машины в таком случае тратят больше времени на «общение», чем на вычисления.

Есть и еще одно решение, которое применяется в машинном обучении для оптимизации, — разреженные матрицы. Это матрицы, которые в основном содержат нулевые элементы. Преимущество заключается в том, что нули в матричных операциях воспринимаются как пустые компоненты. Поэтому такие матрицы расходуют меньше памяти графического процессора. Это ускоряет процедуру машинного обучения, что важно для больших моделей.

Но есть проблема: решения Nvidia, главного поставщика GPU, не поддерживают работу с разреженными матрицами. Но в OpenAI нашли выход из этой ситуации.

Решение от OpenAI

Команда OpenAI разработала программное обеспечение, которое моделирует работу крошечных ядер, способных взаимодействовать с такими матрицами. Ядра опробовали на обучении сетей, анализирующих обзоры на сайтах Amazon и IMDB. Как сообщает команда, уровень ошибок в работе со сводом данных IMDB был снижен с 5,91% до 5,01%.

Ядра реализованы с использованием CUDA, программно-аппаратной архитектуры параллельных вычислений от Nvidia. Но модель OpenAI пока доступна только для TensorFlow. Скотт Грей (Scott Gray), член команды Open AI, сказал, что решение может быть распространено на другие архитектуры, кроме Google TPU2. Компания Nvidia уже знает о работе OpenAI и готова оптимизировать свои системы.

Альтернативные проекты

Концепция разреженных матриц получила свое воплощение в компиляторе с открытым исходным кодом под названием Taco. О проекте, над которым работает команда ученых из Массачусетского технологического института в партнерстве с Adobe Research, стало известно в ноябре. Разработчики искали способ автоматизировать процесс обработки чисел в разреженных матрицах. И использовали для этого тензоры.

О своих разработках в области машинного обучения в декабре отчиталась и компания IBM. Решение ИТ-гиганта — DuHL — предлагает новый метод переноса данных с CPU на GPU. Основная задача технологии — определить, какая информация наиболее важна для алгоритма обучения, и передать её сети в правильном порядке. Исследования показали, что новый подход на основе DuHL в 10 раз быстрее по сравнению с классическим методом последовательной передачи данных между процессорами. Следующая цель компании — предложить DuHL как услугу в облаке.

Но в IBM не первыми придумали переносить GPU-вычисления в облако. Подобные проекты, работающие в том числе по модели IaaS, уже известны. Изначально услугу vGPU предоставляла компания Nvidia. Сейчас этим занимаются и AMD, и Intel.

Об OpenAI

OpenAI — это некоммерческая исследовательская организация, основанная главой Tesla Илоном Маском. Она ставит своей задачей продвижение и развитие искусственного интеллекта на благо человечества. Организация плотно сотрудничает с другими учреждениями и исследователями, предоставляя открытый доступ к своим разработкам.

P.S. Еще несколько материалов из нашего корпоративного блога:

Источник

Введение в разреженные матрицы (sparse matrix)

В одной из статей по Apache Spark я говорил о разреженных (sparse) матрицах, но не вдавался в подробности. Многих сбивают с толку эти разреженные матрицы, поскольку формат их хранения отличается от плотных матриц. Тем не менее, разреженные матрицы очень часто используются в Data Science, поскольку их хранение менее затратное. Сегодня мы шаг за шагом рассмотрим переход от плотных матриц к разреженным, начав со списка координат (COOrdinate list) и закончив сжатым хранением строкой (CSR) и столбцом (CSC).

Локальные векторы: плотные и разреженные

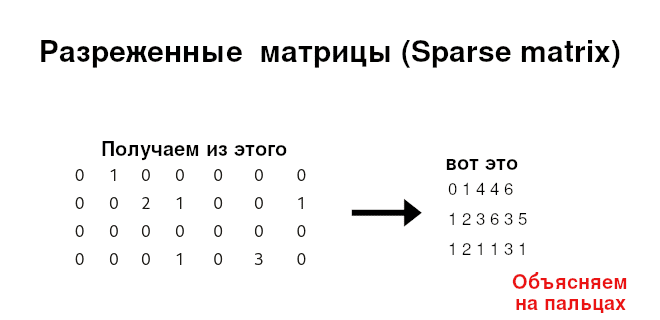
Допустим, что у нас имеется матрица (см. рисунок ниже). При беглом взгляде осознаем, что в ней много нулей (возможно, это матрица c категориальными значениями) А что если бы это была матрица 1000×1000? А матрица 100000×500000 со всеми этими нулями? Нет смысла хранить матрицу, где большая часть элементов – это нули. Поэтому пришли к так называемым разреженным матриц (sparse matrix).

Разреженные матрицы представляют в различных форматах:

• координатный список (Coordinate List),
• сжатое хранение строкой (Compressed Sparse Row),
• сжатое хранение столбцом (Compressed Sparse Column),
• список списков (List of lists),
• словарь ключей (Dict of keys)

Мы расскажем о первых трех, так как они встречаются чаще.

Список координат (Coordinate List)

Возможно, самый очевидный формат хранения разреженных матриц является список координат. Такой формат представляет собой триплет (строка, столбец, значение) . При этом, хранятся только ненулевые значения. Например, матрицу выше можно записать следующим образом:

В этом формате еще хранится размерность матрицы. Подразумевается, что не записанные значения являются нулями.

Улучшаем, применив правило row-major order

Мы можем еще улучшить список координат. Давайте вместо того чтобы хранить каждый индекс строки, будем хранить количество ненулевых значений на каждой строке. Вот, что случится, после применения данного правила:

Подобное правило примененное к строкам называется порядок по строкам (row-major mode). Ничто не мешает применить его к столбцам, тогда это будет порядок по столбцам (column-major order) [1].

Как можно заметить, теперь мы храним меньше данных: в данном примере меньше на два элемента по сравнению с оригинальным списком координат.

А что насчет компьютера? Получается, что он хранит три массива и размерность разреженной матрицы. Тогда как извлечь отдельные строки (поскольку это row-major order) из нее? Алгоритм извлечения p-й строки достаточно прост. Допустим, нам нужна 3-я строка (не забываем про счет с 0), т.е. последняя строка (0,0,0,1,0,3,0) , тогда требуется:

1. Определить количество n ненулевых элементов выше p-й строки. Выполнить эту процедуру путем суммирования элементов в векторе Не-0 в строке вплоть до p-й строки. Для 3-й строки получается 1 + 3 + 0 = 4, значит количество ненулевых элементов выше 3-й строки равно 4.
2. Определить количество k элементов в p-й строке. Это значение равно p-му элементу вектора Не-0 в строке . Для 3-е строки это значение равно 2.
3. Дойти до элемента n + 1 векторов Столбец и Значение . В нашем случае это 4 + 1 = 5.
4. Взять k пар элементов векторов Столбец и Значение . В нашем случае это пары (3, 1) и (5, 3) .
5. Вернуть вектор размера N (где N – это количество строк) с заполненными соответствующими парами, а остальные элементы заполняются нулями. В нашем случае это a[3] = 1 и a[5] = 3 , а все остальное — это нули.

Сжатое хранение строкой (Compressed Sparse Row, CSR)

А что если мы захотим извлечь строку 2-ю, потом 1-ю, потом снова 2-ю и т.д. Исходя из алгоритма, происходит суммирование элементов вектора Не-0 в строке каждый раз при извлечение очередной строки. Так, может быть, сразу и заменим вектор Не-0 в строке на кумулятивную сумму количества ненулевых элементов в строке и назовем новый вектор Кумулята Не-0 в строке . Тогда получится такой результат:

И вот снова требуется получить p-ю строку, например, 3-ю. Тогда алгоритм ее получения будет следующим:

1. Определить количество ненулевых элементов выше p-й строки. Это просто (p — 1)-й элемент вектора Кумулята Не-0 в строке . Для 3-й строки — это 4.
2. Определить количество ненулевых элементов в строке p. Это количество равно разнице между p-м и (p-1)-м элементами вектора Кумулята Не-0 в строке . Для 3-й строки эта разница между 3-м и 2-м элементами, т.е. 6 — 4 = 2.
3. Шаги 3, 4, 5 такие же, как и выше.

В первом шаге нужно добавить условие при извлечении 0-ю строки: Если требуется 0-я строка, вернуть 0 — поскольку выше этой строки ничего нет.

Такой формат хранения называется сжатое хранение строкой (Compressed Sparse Row, CSR).

Сжатое хранение столбцом (Compressed Sparse Column, CSC)

В задачах машинного обучения (machine learning) наиболее распространенной практикой является извлечение столбцов (признаков) нежели строк. С точки зрения математики строки и столбцы матрицы эквивалентны, поэтому правила выше можно применять к столбцам. Такая форма представления называться сжатое хранение столбцом (Compressed Sparse Column, CSC).

Если мы будем считать кумуляту по столбцам, т.е. по правилу порядка по столбцам (column-major order), то получим следующее:

При извлечении столбца считаем то, что левее и правее необходимого. И также возвращается 0 на первом шаге алгоритма при извлечении 0-го столбца.

Еще больше подробностей о векторах, матрицах и других структурах данных с примерами из Data Science вы узнаете на специализированном курсе по машинному обучению «PYML: Введение в машинное обучение на Python» в лицензированном учебном центре обучения и повышения квалификации разработчиков, менеджеров, архитекторов, инженеров, администраторов, Data Scientist’ов и аналитиков Big Data в Москве.

Источник