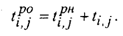Решение сетевой модели графика

3. Пример решения задачи методом сетевого планирования и управления

3.1.Постановка задачи и построение сетевого графика

Издатель имеет контракт с автором на издание его книги. Ниже представлена последовательность (упрощенная) процессов, приводящая к реализации проекта издания книги. Необходимо разработать сеть для этого проекта.

А: Прочтение рукописи редактором

В: Пробная верстка отдельных страниц книги

С: Разработка обложки книги

Е: Просмотр автором редакторских правок и сверстанных страниц

F: Верстка книги (создание макета книги)

G: Проверка автором макета книги

H: Проверка автором иллюстраций

I: Подготовка печатных форм

J:Печать и брошюровка книги

На рис.3.1 показана сеть, представляющая взаимосвязь процессов данного проекта. Фиктивный процесс (2, 3) введен для того, чтобы «развести» конкурирующие процессы А и В. Номера узлов сети возрастают в направлении выполнения проектов.

3.2.Расчет параметров сетевого графика

Определение полных путей и нахождение критического пути.

Найдем полные пути и их продолжительности:

1 путь: 1-2-3-4-6-7-8-9, его продолжительность: 3+0+2+2+2+2+4=15

2 путь: 1-3-4-6-7-8-9, его продолжительность: 2+2+2+2+2+4=14

3 путь: 1-5-7-8-9, его продолжительность: 3+1+2+4=10

4 путь: 1-8-9, его продолжительность: 4+4=8

Критическимв данном случае будет путь 1-2-3-4-6-7-8-9, т.к. его продолжительность максимальна и равна 15. Lкр = 1-2-3-4-6-7-8-9,t(Lкр) = 15.

Для каждого события определим ранний и поздний срок свершения события.

Ранний срок свершения события– это максимальный из путей, предшествующий этому событию.

Поздний срок свершения свершения события Тп(i) определяется разностью между Ткр и длинной максимального из последующих путей.

Резерв времени события равен разности раннего и позднего срока свершения события: R(i) = Тп(i)-Тр(i)

Определяем ранние и поздние сроки начала и окончания работ:

Определяем ранний срок начала работ:

Трн( i, j) = Тр(i)

Определяем ранний срок окончания работ:

Тро( i, j) = Тр(i) + Тij

Тро(8, 9) = Тр(8) + Т89 = 11+4 = 15

Определяем поздний срок начала работ:

Тпн(i, j) = Тп(j) – Тij

Тпн(1, 5) = Тп(5) – Т 15= 13-3 = 10

Тпн(1, 8) = Тп(8) – Т18 = 16-4 = 12

Тпн(4, 6) = Тп(6) – Т 46= 12-2 = 10

Тпн(6, 7) = Тп(7) – Т67 = 14-2 = 12

Тпн(5, 7) = Тп(7) – Т57 = 14-1 = 13

Тпн(7, 8) = Тп(8) – Т 78= 16-2 = 14

Тпн(8, 9) = Тп(9) – Т89 = 20-4 = 16

Определяем поздний срок окончания работ:

Тпо(i, j) = Тп(j)

Определяем полный резерв времени работ:

R(i, j) = Tп(j) – Tp(i) – Tij

R(1, 2) = Тп(2) – Тр(1) – Т12 = 8-0-3 = 5

R(1, 3) = Тп(3) – Тр(1) – Т13 = 8-0-2 = 6

R(1, 5) = Тп(5) – Тр(1) – Т15 =13-0-3 = 10

R(1, 8) = Тп(8) – Тр(1) – Т18 =16-0-4 =12

R(2, 3) = Тп(3) – Тр(2) – Т23 = 8-3-0 = 5

R(3, 4) = Тп(4) – Тр(3) – Т34 =10-3-2 = 5

R(4, 6) = Тп(6) – Тр(4) – Т46 =12-5-2 = 5

R(6, 7) = Тп(7) – Тр(6) – Т67 =14-7-2 = 5

R(5, 7) = Тп(7) – Тр(5) – Т57 =14-3-1 = 10

R(7, 8) = Тп(8) – Тр(7) – Т78 =16-9-2 = 5

R(8, 9) = Тп(9) – Тр(8) – Т89 =20-11-4 = 5

Источник

Задачи сетевого планирования

На этой странице вы найдете решенные типовые задания из контрольных по сетевому планированию — разделу экономико-математических методов и моделей.

В рамках изучения сетевого анализа студенты обычно учатся: строить график сети по табличному или словесному описанию проекта (и наоборот), находить ранние и поздние сроки начала и окончания работ, резервы, критический путь и минимальное времеия завершения проекта. Более сложные задания подразумевают различные варианты корректировки и оптимизации сетевого графика (с увеличением времени и уменьшением затрат, или наоборот, с уменьшением времени и увеличением расходов), задачи распределения ресурсов. Изучаются различные графические способы отображения как сетевого графика (см. задачи ниже), так и других диаграмм для проекта (диаграмма Ганта, линейный график).

Примеры решений задач по сетевому планированию онлайн

Задача 1. Для заданной сетевой модели некоторого комплекса работ определить время и критический путь.

Задача 2. Издатель имеет контракт с автором на издание его книги. Ниже представлена последовательность (упрощенная) процессов, приводящая к реализации проекта издания книги. Необходимо разработать сеть для этого проекта.

Задача 3. 1. По заданному перечню работ, построить сетевой график.
2. Определить продолжительности полных путей графика.
3. Определить и выделить критический путь.
4. Определить резерв времени каждого пути.
5. Определить коэффициенты напряженности пути.
6. Определить ранние и поздние сроки начала и окончания работы.
7. Определить полный резерв времени каждой работы.

Задача 4. Рассчитать параметры сетевого графика (см. таблицу работ в файле).

Задача 5. На сетевом графике найти ранние и поздние сроки наступления событий, определить критический путь и резервы времени каждого события.

Задача 6. Построить сетевой график. Решить задачу оптимального распределения ресурсов по работам при постоянных интенсивностях. Наличие ресурса R=10. Работы не допускают перерыва в их выполнении.

Задача 7. По данным варианта требуется:
1) построить сетевую модель;
2) определить критические пути модели;
3) провести максимально возможное уменьшение сроков выполнения проекта при минимально возможных дополнительных затратах

Источник

Пример построения сетевого графика

Используя полученные данные, мы можем найти основные характеристики сетевой модели табличным методом, критический путь и его продолжительность.
Таблица – Табличный метод расчета сетевого графика.

КПР	Код работы (i,j)	Продолжительность работы t(i, j)	Ранние сроки		Поздние сроки		Резервы времени
			tрн(i,j)	tро(i,j)	tпн(i,j)	tпо(i,j)	Rп	Rc
1	2	3	4	5	6	7	8	9
0	1,2	7	0	7	0	7	0	0
0	1,4	4	0	4	17	21	17	8
0	1,5	3	0	3	19	22	19	0
1	2,3	3	7	10	7	10	0	0
1	2,8	13	7	20	19	32	12	12
1	3,4	2	10	12	19	21	9	0
1	3,6	13	10	23	10	23	0	0
2	4,7	5	12	17	21	26	9	0
1	5,7	4	3	7	22	26	19	10
1	6,8	9	23	32	23	32	0	0
2	7,8	6	17	23	26	32	9	9

Таким образом, работы критического пути (1,2),(2,3),(3,6),(6,8). Продолжительность критического пути Т_кр=32.

Рисунок — Масштабный график сетевой модели
Для оценки вероятности выполнения всего комплекса работ за 30 дней нам необходима следующая формула: P(t_кр где Z=(Т-Т_кр)/S_кр
Z- нормативное отклонение случайной величины, S_кр – среднеквадратическое отклонение, вычисляемое как корень квадратный из дисперсии продолжительности критического пути. Соответствие между Z и Ф(Z) представлено в таблице.
Таблица — Таблица стандартного нормального распределения.

Z	F(Z)	Z	F(Z)	Z	F(Z)
0	0.0000	1.0	0.6827	2.0	0.9643
0.1	0.0797	1.1	0.7287	2.1	0.9722
0.2	0.1585	1.2	0.7699	2.2	0.9786
0.3	0.2358	1.3	0.8064	2.3	0.9836
0.4	0.3108	1.4	0.8385	2.4	0.9876
0.5	0.3829	1.5	0.8664	2.5	0.9907
0.6	0.4515	1.6	0.8904	2.6	0.9931
0.7	0.5161	1.7	0.9104	2.7	0.9949
0.8	0.5763	1.8	0.9281	2.8	0.9963
0.9	0.6319	1.9	0.9545	2.9	0.9973

Критический путь проходит по работам (1,2)(2,3)(3,6)(3,8).
Дисперсия критического пути:
S 2 ­(L_кр)= S 2 (1,2)+ S 2 (2,3)+ S 2 (3,6)+S 2 (6,8)=1+0,25+4+1=6,25
S(L_кр)=2,5
p(t_кр<30)=0,5+0,5Ф((30-32)/2,5)=0,5-0,5Ф(0,8) = 0,5-0,5*0,5763=0,5-0,28815=0,213
Вероятность того, что весь комплекс работ будет выполнен не более чем за 30 дней, составляет 21,3%.
Для определения максимально возможного срока выполнения всего комплекса работ с надежностью 95% будем использовать следующую формулу: T=Т_кр+Z*S_кр Для решения поставленной задачи найдем значение аргумента Z, которое соответствует заданной вероятности 95% (значению графы Ф(Z) 0,9545*100% в таблице 5 соответствует Z=1,9).
T=32+1,9*2,5=36,8
Максимальный срок выполнения всего комплекса работ при заданном уровне вероятности 95% составляет всего 36,8 дня.

Источник

7.8. Расчет сетевых моделей непосредственно на графике

Метод расчёта сетевых моделей непосредственно на её графиче­ском представлении используется в том случае, когда количество со­бытий в сетевой модели небольшое.

Пусть имеется та же сетевая модель, которую мы рассчитали табличным методом:

Для расчета сетевой модели непосредственно на графике, каж­дое событие делят на четыре сектора (А, Б, В, Г), в которых указывают следующие данные:

Б — раннее начало работ, выходящих из рассматриваемого события;

В — позднее окончание работ, входящих в рассматривае­мое событие;

Г- номер события, из которого к данному идет максимальный путь.

Алгоритм расчета

1. Расчет ранних начал работ осуществляется на графической модели слева направо. Данные расчета записываются в секторе Б.

1.1. Раннее начало работ, выходящих из исходного события, равно нулю. Номер события, из которого к данному идет максималь­ный путь, также равен нулю, т. к. предшествующего события нет.

1.2. Для каждого следующего события в его секторе Б записы­вают раннее начало работ, выходящих из него. Если в рассматривае­мое событие входит одна работа, то это значение равно раннему на­чалу входящей работы плюс ее продолжительность:

Если же в рассматриваемое событие входят несколько работ, то раннее начало выходящих из него работ равно максимальному из окончаний всех входящих в него работ:

Например, для события 2 в его секторе Б записывают 2, т. к. max (0 + 2) = 2. Для события 3 записывают 5, т. к.: мах(2 + 3; 0 +4) = 5.

2. Одновременно в секторе Г рассматриваемого события запи­сывают номер события, из которого к данному событию идет макси­мальный путь. Например, для события 2 максимальный путь идет из события 1, а для события 3 — из события 2.

3. Расчет поздних окончаний работ выполняют, начиная из за­вершающего события до начального.

3.1. Для завершающего события j (в нашем случае j = 7) позднее окончание входящих в него работ равно максимальному значению из ранних окончаний всех входящих в событие j работ:

Здесь maxj читается так: максимальное значение из входящих в событие j работ. В нашем случае, позднее окончание работ, входящих з событие7 = 7, равно:

для работы 6 — 7 : 14 + 1 = 15;

3.2. Позднее окончание работ, выходящих из других событий, оп­ределяется следующим образом:

а) если из рассматриваемого события выходит одна работа, то позднее окончание всех входящих в это событие работ равно поздне­му окончанию выходящей из него работы минус ее продолжитель­ность:

Например, для события № 6 позднее окончание работ 2-6 и 5-6 эавно 17-1 = 16;

б) если же из рассматриваемого события выходит несколько ра­бот, то позднее окончание всех входящих в данное событие работ эавно минимальному из значений разности позднего окончания выхо­дящих работ и их продолжительности:

Например, для события № 4 позднее окончание работы 1- 4 -авно min(13 — 2; 17 — 9) = 8.

4. Критический путь по направлению к исходному событию называет номер события, из которого к рассматриваемому событию см. значение сектора Г рассматриваемого события) идет максималь­ный путь. Если рассматривать путь от завершающего события, то он роходит через те события /, в которых раннее начало выходящих из его работ и позднее окончание входящих в него работ (секторыБиВ -обытий) равны:

5. Общий резерв времени каждой работы, как уже указывалось выше, равен:

Так как значение tf°-, при использовании этого метода, не опре­деляется, то его необходимо заменить на

Например, для работы 2 — 5: R2-5 = 13-2-6 = 5.

6. Частный резерв времени, как было показано ранее, равен разности между ранним началом последующих работ и ранним окон­чанием рассматриваемой работы:

Заменив, как в случае определения общего резерва, , получим окончательную формулу расчёта частного резерва времени рассматриваемым методом:

Например, для работы 2-6: =14-2-5 = 7.

Источник