Ступин Андрей Анатольевич
Анализ сетевого графика, опирающийся на результаты расчетов, включает оценку целесообразности структуры графика, загрузки исполнителей работ на всех этапах выполнения проекта, возможности смещения начала работ некритической зоны и, наконец, оценку вероятности наступления события в заданный срок.
Одним из первых шагов анализа построенного графика является пересмотр топологии сети, который заключается не только в контроле правильности построения графика, но и в установлении целесообразности детализации работ и структуры сети. При этом наряду с установлением лишних работ и проверкой целесообразности установленного уровня детализации должен быть рассмотрен вопрос о возможности параллельного выполнения работ исходя из особенностей планируемого процесса и имеющегося количества работников.
Вторым этапом анализа может быть классификация и группирование работ по величинам резервов (полных и свободных). При этом следует подчеркнуть, что далеко не всегда величина полного резерва может достаточно точно характеризовать, насколько напряженным является выполнение той или иной работы некритической зоны. Все зависит от того, на какую последовательность работ распространяется вычисленный резерв, какова величина (протяженность) этой последовательности. Иными словами, важно не только абсолютное, но и относительное значение резерва работы или отрезка пути.
Определить степень трудности выполнения в срок каждой группы работ некритического пути можно с помощью коэффициентов напряженности работ.
Коэффициент напряженности работ — это отношение продолжительности отрезка наибольшего из некритических путей, проходящих через данную работу, к продолжительности несовпадающего отрезка критического пути, проходящего через эту работу.
Если сопадающую с критическим путем величину отрезка пути обозначить как
длину критического пути —
а протя-
женность максимального из некритических путей, проходящих через данную работу, —то коэффициент напряженности работы
(11,11)
Формулу можно выразить через резерв времени:
(1112)
Чем выше коэффициент напряженности, тем сложнее выполнить данную работу в установленные сроки. И наоборот, чем меньше коэффициент напряженности, тем большими относительными резервами обладает данный путь в сети.
Расчет коэффициентов напряженности позволяет заново проанализировать топологию сети в отношении выравнивания коэффициентов напряженности путей. По полученным таким образом коэффициентам напряженности все работы распределяются по зонам: критическая, подкритичесая и резервная.
Критическая зона сетевого графика — это совокупность путей, включая критический, абсолютные значения резервов времени которых меньше заданной величины, то естьблизкие к единице.
Резервная зона — это совокупность работ, имеющих значение значительно меньше единицы.
Следующим этапом анализа является расчет вероятностных характеристик сетевых моделей.
Расчет вероятности наступления завершающего события в заданный срок оказывается особенно необходимым, когда установ-пенный директивный срок Та оказывается меньше расчетного срока Тк. Если предположить, что срок окончания работ является случайной нормально распределенной величиной, то вероятность выпол- ! нения работ в директивный срок
(11.13)
Вначале определяем значение и, а затем по таблице приложения 4 функции Лапласа— вероятность выполнения работ в директивный срок.
Здесь — дисперсия г’-й работы критического пути; п — число работ критического пути.
Для величины
устанавливаются вполне определенные пределы, именуемые границами допустимого риска. По данным практики выполнения работ по графикам, при 
можно утверждать, что на работах критического пути имеются избыточные ресурсы, следовательно, общая продолжительность работ может быть сокращена. При
опасность срыва заданного срока выполнения работ очень велика и необходимо повторное планирование с перераспределением ресурсов.
Оптимизация сетевого графика представляет собой процесс улучшения организации выполнения комплекса работ с учетом установленного срока и использования ресурсов. Она осуществляется за счет:
а) перераспределения ресурсов как временных, так и других;
б) интенсификация выполнения работ критического пути;
в) изменений в характере комплекса работ.
При минимизации времени выполнения работ общий срок выполнения следует сокращать в первую очередь за счет изменения продолжительности критических работ. Выделение дополнительных ресурсов для критических работ, естественно, представляется более привлекательным, чем их интенсификация.
Отработанная сетевая модель выполнения работ далее может быть преобразована в календарный график.
Коэффициент напряженности работ.
Анализ сетевого графика начинается с анализа структуры сети, включающего контроль построения сетевого графика, устранение целесообразности выбора работ, степени их расчленения. Затем проводится классификация и группировка работ по выявлению резервов, с тем, чтобы определить степень трудности выполнения в срок каждой группы работ. Величина полного резерва времени не всегда может достаточно точно характеризовать, насколько напряженным является выполнение той или иной работы некритического пути. Все зависит от того, на какую последовательность работ распространяется вычисленный резерв, какова продолжительность этой последовательности. Определить степень трудности выполнения в срок каждой группы работ некритического пути можно с помощью коэффициента напряженности работ. Коэффициентом напряженностиКНработы(i,j) называют отношение продолжительности несовпадающих (заключенных между одними и теми же событиями) отрезков пути, одним из которых является путь максимальной продолжительности, проходящий через данную работу, а другим – критический путь: КН(i,j)=
(12) где: 
— продолжительность максимального пути, проходящего через работу (i, j); 
— продолжительность отрезка рассматриваемого пути, совпадающего с критическим путем; 
— продолжительность (длина) критического пути. Находим коэффициент напряженности работы (1;2): Максимальный путь, проходящий через работу (1;2) – это путь 0→1→2→10→11→12→13→14→15. Продолжительность: 1+1+2+3+3+30+10+5=55. Продолжительность отрезка пути, совпадающего с критическим путем: 3+3+30+10+5=51. Подставим найденные значения в формулу: Кн(1;2)= 
Находим коэффициент напряженности работы (3;6): Максимальный путь, проходящий через работу (3;6) – это путь 0→3→6→11→12→13→14→15. Продолжительность: 4+5+1+3+30+10+5=58. Продолжительность отрезка пути, совпадающего с критическим путем: 3+30+10+5=48. Подставим найденные значения в формулу: Кн(3;6)= 
Находим коэффициент напряженности работы (4;7): Максимальный путь, проходящий через работу (4;7) – это путь 0→4→7→9→12→13→14→15. Продолжительность: 3+2+5+2+30+10+5=57. Продолжительность отрезка пути, совпадающего с критическим путем: 30+10+5=45. Подставим найденные значения в формулу: Кн(4;7)= 
Коэффициент напряженности КН(i, j) может изменяться в пределах от 0 (для работ, у которых отрезки максимального из путей, не совпадающие с критическим путем, состоят из фиктивных работ нулевой продолжительности) до 1 (для работ критического пути). Чем ближе к 1 коэффициент напряженности, тем сложнее выполнять данную работу в установленные сроки, а чем ближе он к нулю, тем большим относительным резервом обладает максимальный путь, проходящий через данную работу. Работы могут обладать одинаковыми полными резервами, но разной степенью напряженности. И наоборот, различным полным резервам могут соответствовать одинаковые коэффициенты напряженности. Из формулы (13) видно, что величина коэффициента напряженности зависит от RП и 
. Чем полный резерв времени RП больше выполнения некоторой работы и 
, (то есть чем меньше
—
— отрезок времени максимального пути, проходящего через эту работу и не совпадающего с критическим путем), тем больше будет дробь, стоящая в правой части формулы (13), и тем меньше коэффициент напряженности этой работы, тем легче будет ее выполнить. В общем случае указанная дробь определяет удельный вес полных резервов времени работ в продолжительности отрезков максимальных путей, не совпадающих с критическим путем. Чем больше этот удельный вес, тем меньше коэффициент напряженности. Выделяют следующие зоны: -критическая: Кн(i;j)>0,8 -подкритическая: 0,60,8 (0,4) попадает в критическую зону, так как Кн(0,3)=0,9>0,8 (3,6) попадает в критическую зону, так как Кн(3,6)=0,9>0,8 (4,7) попадает в критическую зону, так как Кн(4.7)=0,9>0,8 (2,10) попадает в резервную зону, так как Кн(2,10)=0,50,8 (7,8) попадает в критическую зону, так как Кн(7,8)=0,9>0,8 (7,9) попадает в критическую зону, так как Кн(7,9)=0,9>0,8 (8,9) попадает в критическую зону, так как Кн(8,9)=0,9>0,8 (9,12) попадает в критическую зону, так как Кн(9,12)=0,9>0,8 ЗАКЛЮЧЕНИЕ: Искусство экономико-математического моделирования состоит в выполнении двух противоречивых между собой требований:
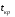
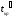
- с одной стороны, заменить сложный экономический объект его математической моделью для облегчения проводимых исследований;
- с другой стороны, обеспечить адекватность математической модели моделируемому экономическому объекту.
В данной курсовой работе был построен сетевой график по предприятию «ЗАО Авто-агрегат центр» г. Наб. Челны, проведен его анализ, и произведена оптимизация сетевого графика. Рациональность данных методик заключается в том, что они позволяют найти критический путь сетевого графика. При построении сетевого график был определен критический путь проекта, составляющий 59 дня. Произведено решение двух основных задач сетевого планирования: задачу анализа оптимальности уже готового сетевого графика и задачу его оптимизации по длительности. Заключение анализа сетевого графика состоит в том, чтобы выявить резервы времени работ, не лежащих на критическом пути, и направить их на работы, лимитирующие срок завершения комплекса работ. Результатом этого является сокращение продолжительности критического пути. Сетевое планирование при реализации сложных проектов увеличивает эффективность работ и способствует уменьшению затрат. Решение экономических задач с помощью метода математического моделирования позволяет осуществлять эффективное управление как отдельными производственными процессами на уровне прогнозирования и планирования экономических ситуаций и принятия на основе этого управленческих решений, так и всей экономикой в целом.
Для продолжения скачивания необходимо пройти капчу: