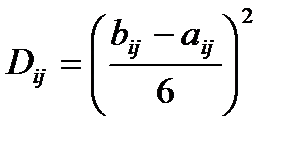Формы представления сетевой модели.
В курсе «Математические методы и модели в таможенном деле» рассматриваются математические методы и модели, позволяющие решать различные задачи, встречающиеся в таможенном деле. Методы сетевого планирования и управления позволяют осуществлять оптимальное планирование сложного комплекса работ: формировать различные виды их представления в виде моделей, осуществлять расчет характеристик и оптимизацию комплекса работ.
Здесь же изложены вероятностные модели сложных систем и модели массового обслуживания. Рассматриваются различные математические модели систем массового обслуживания и методы решения задач на их основе. Представлены системы управления запасами, разбираются алгоритмы решения задач управления запасами. Изложена сущность игровых задач.
МЕТОДЫ И МОДЕЛИ СЕТЕВОГО ПЛАНИРОВАНИЯ И УПРАВЛЕНИЯ
При управлении разработками сложных программ и системами возникает задача рационального планирования и координации большого комплекса различных работ (операций, действий).
Характерным для сложных комплексов связанных между собой работ является то, что отдельные работы не могут быть выполнены независимо друг от друга, выполнение ряда работ не может быть начато раньше, чем завершены другие.
Системы сетевого планирования и управления (СПУ) обеспечивают системный подход к решению вопросов организации управления, то есть рассмотрение всего комплекса работ как единого неразрывного комплекса взаимосвязанных работ, направленных на достижение общей конечной цели. Логико-математическое описание, формирование планов и управляющих воздействий осуществляются на базе использования особого класса моделей, называемых сетевыми моделями.
Ориентированный граф, в котором существует лишь одна вершина, не имеющая входящих дуг, и лишь одна вершина, не имеющая выходящих дуг, называется сетью. Сеть, моделирующая комплекс работ, называется его сетевой моделью или сетевым графиком. Дуги, соединяющие вершины графа, ориентированы в направлении достижения результата при осуществлении комплекса работ.
Наиболее распространен способ представления моделируемого комплекса работ в понятиях работ и событий.
Понятие «работа» имеет следующие значения:
– «действительная работа» – процесс, требующий затрат времени и ресурсов;
– «фиктивная работа» – логическая связь между двумя или несколькими работами, указывающая на то, что начало одной работы зависит от результатов другой. Фиктивная работа не требует затрат времени и ресурсов, продолжительность ее равна нулю.
На сетевых моделях работам соответствуют дуги, причем действительные работы изображаются сплошными линиями, а фиктивные – пунктирными.
Понятие «событие» означает факт получения результата вследствие завершения одной или нескольких работ. Каждая работа заключена между двумя событиями, так как с события, завершающего одну или несколько работ, начинаются другие работы. Событие может наступить только тогда, когда окончатся все предшествующие ему работы.
Событие, с которого начинается выполнение всех работ комплекса, называется исходным. Исходное событие не имеет предшествующих ему работ и событий.
Событие, которым заканчивается весь комплекс работ, называется завершающим. Завершающее событие не имеет последующих работ и событий.
Событие, непосредственно предшествующее работе (с которого начинается работа), называется начальным, а непосредственно следующее за ней (которым заканчивается работа) – конечным.
На сетевой модели событиям соответствуют вершины графа.
Любая последовательность работ в сетевой модели, в которой конечное событие одной работы совпадает с начальным событием следующей за ней работы, называется путем. Путь от исходного события до завершающего называется полным путем.
Каждой дуге сетевой модели приписывают число, которое называется длиной дуги. Соответственно длиной пути называется сумма длин последовательности дуг, составляющих данный путь. Длина дуги выражает время, необходимое для выполнения работы, представленной данной дугой. Поэтому длина пути (или продолжительность пути) есть суммарная продолжительность работ, составляющих данный путь.
Начальная информация, необходимая для построения сетевой модели, должна содержать перечень всех работ и последовательность их выполнения, то есть отношения непосредственного предшествования между работами комплекса.
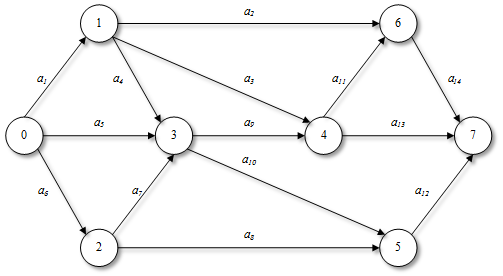
Пусть информация о комплексе работ задана табл.1, в которой работы условно обозначены символами а 1, a 2, …. Из таблицы видно, что работы а 1, а 5, а 6 не имеют предшествующих, поэтому в сетевой модели дуги, соответствующие этим работам, будут выходить из исходного события комплекса. Работы а 12, a 13, a 14 не предшествуют никаким другим работам, и поэтому дуги, соответствующие этим работам, будут входить в завершающее событие комплекса. Конечное событие работы а 1 является начальным событием для работ a 2, a 2, a 2; конечное событие для работы a 2 является начальным для работы a 14 и так далее. Сетевой график комплекса изображен на рис. 1.
Работы (дуги) на сетевых графиках обозначают символами (i, j), где i – номер начального события работы, а j – номер конечного события. События должны быть пронумерованы так, чтобы для любой работы (в том числе и фиктивной) всегда i < j. Для получения такой нумерации применяется метод разделения событий на ранги. Сущность метода заключается в следующем.
Исходному событию присваивается нулевой ранг. Вычеркнув все дуги, выходящие из исходного, получим несколько (или, по крайней мере, одно) событий без входных дуг. Этим событиям присваивается первый ранг. Вычеркнув все дуги, выходящие из событий первого ранга, снова получим события без входящих дуг, которым присваивается второй ранг. Вычеркнув далее все дуги, выходящие из событий второго ранга, получим события без входящих дуг, которым присваивается третий ранг, и так далее.
Легко видеть, что событие любого ранга связано с событием предшествующего ранга одной дугой. Следовательно, событие k- го ранга обязательно связано с исходным событием путем, состоящим из k дуг; хотя, кроме того, событие k- горанга может быть соединено с исходным событием и путем, состоящим из меньшего числа дуг. Так, например, событие 6 на сетевом графике рис. 1 связано с исходным событием тремя путями: 1) путем, состоящим из дуг (0, 1), (1, 6); 2) путем, состоящим из дуг (0, 3), (3, 4), (4, 6) и 3) путем, состоящим из дуг (0, 1), (1, 3), (3, 4), (4, 6). Ранг события 6 равен 4, так как последний путь содержит максимальное число дуг, равное 4.
Таблица 1 Комплекс работа
| Работа | Каким работам непосредственно предшествует |
| а1 | а2, а3, а4 |
| а2 | а14 |
| а3 | а11, а13 |
| а4 | а9, а10 |
| а5 | а9, а10 |
| а6 | а7, а8 |
| а7 | а9, а10 |
| а8 | а12 |
| а9 | а11, а13 |
| а10 | а12 |
| а11 | а14 |
| а12 | — |
| а13 | — |
| а14 | — |
Событию присваивается ранг k, если максимальное число дуг пути, соединяющего его с исходным равно k.
После распределения всех событий по рангам нумерация осуществляется следующим образом. Исходное событие нулевого ранга получает номер 0. Событиям первого ранга в произвольном порядке присваивают номера 1, 2, …, n 1, где п 1 – число событий первого ранга; события второго ранга получают номера n 1+1, n 1+2. n 1+ n 2 где п 2 – число событий второго ранга, и так далее.
Так как события одного ранга между собой не соединены, а события меньшего ранга имеют меньший номер, то для любой дуги (i, j) всегда i < j.
Рассмотренный метод нумерации событий называют методом последовательного вычеркивания дуг.
Заметим, что нумерация событий, при которой для любой дуги (i, j) всегда i < j, обязательна при машинных методах расчета параметров сетевых моделей.
В зависимости от задач управления в системах СПУ применяют различные типы сетевых моделей, отличающиеся составом информации о комплексе работ. Среди них можно выделить два основных типа: модели с учетом только временных характеристик (ограничения на ресурсы не накладываются) и модели с учетом временных и ресурсных характеристик.
Модели первого типа не являются оптимизационными. Но, несмотря на это, их применение в системах СПУ позволяет эффективно решать существенные проблемы управления, а именно – найти минимальное время, в течение которого может быть выполнен весь комплекс, и определить календарные сроки начала и окончания каждой работы комплекса, обеспечивающие выполнение всего комплекса в найденное минимальное время.
Модели второго типа относятся к задачам распределения ресурсов. Эти задачи являются оптимизационными и встречаются в разных постановках. В зависимости от принятого критерия оптимальности и характера ограничений их можно разбить на две основные группы:
– задачи минимизации сроков наступления завершающего события при соблюдении заданных ограничений на использование ресурсов;
– задачи оптимизации некоторого показателя качества использования ресурсов при заданных сроках выполнения комплекса. К этой группе относится, в частности, задача минимизации ресурсов при заданном времени выполнения комплекса.
Основной временной характеристикой комплекса работ и каждой отдельной работы является их продолжительность. Оценки продолжительности выполнения отдельных работ могут быть детерминированными и вероятностными. В первом случае сетевая модель называется детерминированной, во втором – вероятностной.
Сетевые модели могут быть также смешанными, поскольку для некоторых работ могут существовать детерминированные оценки, а для некоторых вероятностные.
Продолжительность работы (i, j) обозначают через tij. Оценка величины tij может производиться:
– по действующим нормативам;
– по накопленным данным с достаточно высоким процентом повторяемости работ;
– методом экспертных оценок;
– на основе вероятностных оценок.
На основании статистических данных установлено, что распределение случайной величины tij определяется так называемым бета-распределением. Это распределение имеет место в тех случаях, когда случайная величина зависит от большого числа случайных факторов, оказывающих незначительное влияние, и от нескольких существенно влияющих факторов.
В системах СПУ используются три вероятностные оценки:
aij – минимальное время, необходимое для выполнения работы при наиболее благоприятных условиях;
bij – максимальное время, необходимое для выполнения работы при наименее благоприятных условиях;
mij – наиболее вероятное время выполнения работы при нормальных, наиболее часто встречающихся условиях.
Все эти оценки даются ответственными исполнителями или экспертами.
Величины aij,bij и mij используются для вычисления ожидаемого значения продолжительности работы t̅ij, представляющего собой математическое ожидание случайной величины tij, и дисперсии Dij. Полученные значения t̅ij и Dij являются характеристиками случайной величины tij, распределенной по закону бета-распределения.
В системах СПУ наиболее широко применяются следующие расчетные формулы указанных параметров:
(1)
(2)
(3)
(4)
По степени охвата работ различают первичные, частные и комплексные сетевые модели.
Первичные сетевые модели представляют собой детализированные изображения частей комплекса и составляются ответственными исполнителями работ. Частные сетевые модели строятся на основе первичных. Сшивание частной модели заключается в объединении первичных моделей в общую модель, завершающее событие (события) которой соответствует заданной частной цели (целям). Для сшивания частной модели необходимо строго установить идентичность граничных событий в первичных сетевых моделях.
Комплексная (сводная) сетевая модель охватывает все работы комплекса. Сшивание комплексной модели производится аналогично сшиванию частных моделей.
На высоких уровнях управления неудобно пользоваться детализированными сетевыми моделями, поэтому производится их укрупнение. При укрупнении модели должны соблюдаться следующие правила:
– участок модели (группа взаимосвязанных работ) может быть заменен одной укрупненной работой, если этот участок имеет одно исходное и одно завершающее событие. Продолжительность такой укрупненной работы равна продолжительности критического пути данной группы работ;
– нельзя вводить в укрупненную модель события, которых нет в детализированной модели;
– исходное и завершающее события в детализированной и укрупненной моделях должны иметь одинаковый смысл;
– объединять в одну работу следует только такие группы работ, которые закреплены за одним ответственным исполнителем.
Формы представления сетевой модели.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: