5.1. ОСНОВЫ ТЕОРИИ ГРАФОВ И СЕТЕВЫЕ МОДЕЛИ
5.1.1. Общие замечания, основные понятия и определения
Графы представляют собой наиболее абстрактную струк туру, с которой приходится сталкиваться в курсах математиче ской логики, дискретной математики, теории сетей связи. Любая система, предполагающая наличие дискретных состояний или узлов и переходов между ними, может быть описана графом. Характерным примером этого является построение ориентиро ванного графа для эквивалентных схем моделей макроуровня в п. 2.2.4 раздела 2 настоящего пособия. Граф — это совокупность вершин (узлов) и связывающих их ребер (ветвей). Графы отображаются на плоскости набором точек и соединяющих их линий или векторов. При этом ветви могут отображаться и кривыми линиями, а их длина не играет никакой роли. Граф называется ориентированным (или оргра фом ), если некоторые ребра имеют определенное направление. Это означает, что в орграфе некоторая вершина может быть со единена с другой вершиной, а обратного соединения нет. Ребра орграфа называются дугами. Смежные вершины графа — вершины, инцидентные одно му и тому же ребру (принадлежащие одному ребру). Ребро гра фа определяется парой вершин. Два ребра, инцидентные одной и той же вершине (у которых есть общая вершина), также назы ваются смежными (или соседними).
поток вдоль каждой дуги ограничен. В этом разделе формули руются основные принципы и излагается метод решения ука занного класса сетевых задач.
5.1.2. Решение задачи о максимальном потоке
Задача максимального потока формулируется следующим образом. Пусть каждой дуге (п„ nj) сети G = (1 V, А) поставлено в со ответствие некоторое неотрицательное вещественное число сц, называемое пропускной способностью дуги. Выделим на сети два узла: пх и п,, которые назовем источником и стоком соот ветственно. Тогда потоком величины F из л, в п, называется функция х, отображающая А на множество неотрицательных
| вещественных чисел и удовлетворяющая условиям: | |||
| F, если л( = л. | |||
| X | X *, • 0, если и, * и,,и,, | (5.1) | |
| (flf.MyJe/f | (л,,лу)еД» | -F , если л( = и, | |
| Ху | (5.2) | ||
где А* — множество дуг с начальным узлом л„ а А~ — множест во дуг с конечным узлом nt. Величина х,у называется потоком по Дуге («,,/)- Уравнение (5.1) показывает, что суммарный поток из каж дого промежуточного узла равен 0, а суммарный поток в сток равен F. Из уравнения (5.2) следует, что поток по каждой дуге не превышает ее пропускной способности. Максимальным по током из лд в п, назовем такую функцию х, удовлетворяющую представленным уравнениям, для которой величина F макси мальна. Пример потока в сети дан на рис. 5.2, на котором первое число, поставленное в соответствие каждой дуге — ее пропуск
ная способность, а второе — поток по дуге. Жирными линиями выделены насыщенные дуги, т.е. те, поток по которым равен их пропускной способности. Рис. 5.2. Поток в сети (величиной F = 5) Физически поток можно представить как количество ус ловного «груза», перевозимого из вершины с номером / в вер шину с номером у, а суммарный поток F — как количество груза, перевозимого из источника в сток. Введем следующие обозначения: пусть Р и Q — два под множества множества узлов N сети G = (N, А), тогда (Р, Q) обо значает множество всех дуг с начальным узлом в Р и конечным в Q. Обозначим также:
| x (P ,Q )= ‘£ x 0 , | (5-3) |
| п,еР | |
| njeQ | |
| с ( Л 0 = 2 > * | (5.4) |
| п,еР | |
| njcQ |
Разобьем теперь N на два непересекающихся множества: Р, содержащее источник пх, и дополнительное к нему Р , содер жащее сток п,. Разрезом сети G, отделяющим источник от стока, назовем множество дуг (Р, Р ), т.е. множество дуг, на чальные вершины которых принадлежат множеству Р, а конеч ные — множеству Р
Очевидно, что, убрав из G все дуги, принадлежащие неко торому разрезу, мы полностью изолируем источник от стока. Например, жирная пунктирная линия на рис. 3 изображает раз рез, отделяющий ns от и,; здесь Р = <пи п2, Щ, п4>, ? = и(Р, Р )= <(л,, и5), (и3, п5), (л4, л6)>. Заметим, что дуга (л5, щ) принадлежит к ( Р , Р), но не к (Р, Р ), поскольку ее начало от носится к множеству Р Величину с (Р, Р ) назовем пропускной способностью разреза (Р, Р ). Так, разрез на рис. 5.2 имеет пропускную спо
| собность 9. Просуммируем теперь уравнения | (5.1) для всех |
| п, е Р. Проведя сокращения, получим: | |
| F = x(P ,P )-x(P ,P ). | (5.5) |
| Так как все JC ^-> 0, то х(Р, Р ) > 0; из (5.3) и (5.4) следует | |
| также, что х(Р, Р ) < с(Р, Р ), следовательно, | |
| F | (5.6) |
Иными словами, соотношение (5.6) утверждает, что для произвольного потока и произвольного разреза величина потока всегда не больше пропускной способности разреза. Этот резуль тат довольно очевиден, но он имеет важное следствие. Если мы найдем такой поток х и такой разрез (Р, Р ), что F = с(Р , Р ), то мы можем быть уверены, что поток х максимален, а разрез
Каждой дуге (и„ и,) е А в сети G'( х) соответствует: 1. Нормальная дуга (и„ и7), если в G Хц < су и xJt = 0 (или (п„ nj) £ А). 2. Обращенная дуга (и,, л,), если в Gx,j >0. Очевидно, что при условии неотрицательности потоков вто рому условию соответствуют все дуги сети, т.е. обращенная дуга должна быть поставлена в соответствие каждой исходной дуге. Зададим следующие пропускные способности дуг присое диненной сети G'(x). Для каждой нормальной дуги (и„ nj) поло жим с’ у=|Хц — Су\, а для каждой обращенной дуги (и7, «,) Заметим, что по построению каждой дуге сети G'(x) соответст вует определенная дуга из G, имеющая те же конечные узлы. Ориентация этих дуг совпадает, если дуга из G'(x) нормальная, и противоположна, если дуга из G'(x) обращенная. На рис. 5.3 показана сеть, присоединенная к потоку в сети рис. 5.2. На рис. 5.3 обращенные дуги изображены пунктирными линиями, числа на дугах показывают их пропускные способности. Предположим теперь, что на сети G'(x) существует некий путь (г из иЛв и, и пусть Д — минимум с’у, взятый по множеству дуг этого пути. Тогда путь р определяет цепь у из ид в п, на се ти G. (Каждой нормальной дуге р соответствует прямая дуга у, а каждой обращенной дуге р соответствует обратная дуга у).
Увеличим теперь в G (исходной сети) поток х на величину Д в каждой прямой дуге цепи у и уменьшим его на ту же величи ну в каждой обратной дуге этой цепи. Понятно, что увеличение можно производить только для дуг, которые не являются насы щенными. Легко видеть, что при этом не будут нарушены огра ничения (5.2), суммарный поток из каждого промежуточного узла останется равным нулю, а поток из источника в сток увели чится на А. Следовательно, мы получим в исходной сети новый поток х’ величины F + Д; так, например, присоединенная сеть
| (рис. 5.4) содержит путь | |
| Ц = («ь из), (из, п2), ( п 2, п5), (и5, п6), | (5.7) |
| для которого А = 2. Соответствующая модификация | потока |
(см. рис. 5.2) (F = 5) приведет нас к новому потоку величины 7, изображенному на рис. 5.4. Рис. 5.4. Поток в сети величины 7 (максимальный поток) Предположим теперь, что сеть G'(x) не содержит ни одно го пути из ns в Н/. Пусть Р — подмножество М, состоящее из ns и всех узлов, достижимых из ял, т.е. лежащих на путях, исходя щих из пя. Тогда ns е Р и nt е Р , (Р, Р ) является разрезом G, отделяющим пх от nt. На каждой дуге (я/, nj) е(Р, Р) поток должен быть нулевым. Иначе G'(x) содержала бы обращенную Дугу (н/, л,), делающую узел п7е Р достижимым из ns. Анало гично каждая дуга (w„ nj) е (i5, Р ) должна быть насыщенной, иначе G'(x) содержала бы нормальную дугу (л„ nj), делающую
| узел и, € Р достижимым из ns. Следовательно, х | ( Р , Р,) =О, |
| л:(Р, Р ) = с(Р, Р ), откуда имеем | |
| F = х(Р, Р) — JC (P, Р) = с(Р, Р ) . | (5.8) |
Таким образом, как следует из (5.4) и (5.6), х — макси мальный поток, а (Р, Р ) — разрез G минимальной пропускной способности. На рис 5.5 изображена присоединенная сеть G'(x), где*- поток в сети рис. 5.4. На рис 5.5 нет пути из источника к стоку и Р = < п 1 , из>, Р = — Пунктирная линия на рис. 5.5 показывает соответствующий разрез
| (Р, Р ) = | (5.9) |
с пропускной способностью 7, равной величине потока. Рис. 5.5. Присоединенная сеть при найденном максимальном потоке Итак, мы доказали следующие утверждения: 1. Поток в сети G максимален тогда и только тогда , ко гда присоединенная сеть G'(x) не содержит ни одного пути из источника в сток . 2. Теорему о максимальном потоке и минимальном разре зе: для любой сети максимальная величина потока от источни ка к стоку равна минимальной пропускной способности разреза , отделяющего источник от стока.
Сети. Сетевые модели представления информации
В этом проглядывается талант исследователя охватить значительные районы явлений с помощью немногочисленных допущений, представить разносторонние совокупности предметов и процессов в сжатой, компактной форме.
Граф называется взвешенным или сетью, если каждому его ребру поставлено в соответствие некоторое число (вес). Взвешенными графами могут быть схемы в электронике, электрические схемы, карты автомобильных и железных дорог и др. Например, на картах автодорог вершины являются населенными пунктами, ребра — дорогами, а весом — числа, равные расстоянию между населенными пунктами.
В строительстве сетевые графы применяются для наглядного изображения некоторого комплекса работ или производственных процессов. Ребрам графа могут соответствовать числа, означающие длину, уклон, запланированное время и другие характеристики.
Например, последовательность работ для монтажа каркаса здания изображена в виде графа (рис. 2.20).
Числами обозначены технологические операции:
3 — завоз металлоконструкций;
4 — монтаж подъемного крана;
На рис. 2.21 изображен сетевой граф некоторого комплекса раб в виде взвешенного графа с указанием времени, затраченного выполнение этой работы (в минутах).
В основе процесса планирования лежит некоторый сценарл представляющий собой сеть, состоящую из вершин — пошагового описания действий и дуг — отношений между ними. Такой дает возможность, сравнивая альтернативы, планировать действия для достижения поставленной цели.
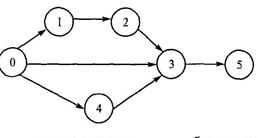 |
| Рис. 2.20. Диаграмма последовательности работ при строительстве здания |
Сети широко используются в качестве моделей для представления знаний в интеллектуальных системах. Сетевая модель представления информации основана на том, что любые знания можно рассматривать как множества объектов (понятий) и связи между ними (отношения).
Понятия-объекты и другие элементы предметной области могут быть графически изображены в виде вершин, а отношения между ними — в виде дуг, связывающих эти вершины. Такое физическое представление информации (знаний) в интеллектуальных системах носит название семантических сетей. Они являются универсальным средством для представления знаний в интеллектуальных системах. Понятия, входящие в сети, можно описать с помощью фрейма. Фреймом называется минимально возможное описание сущности некоторого явления, объекта, события процесса. Состоит фрейм из набора стандартных единиц — слотов, содержащих определенный минимум информации о его содержании и назначении. Семантическая сеть в виде некоторой ее совокупности фреймов нуждается в указании отношения междуеевершинами, что тоже возможно осуществить в виде слота. Семантические сети широко применяются в информатике, например, для операций поиска по образцу, где в виде сетей представляется база данных. Результат такого поиска можно изобразить графом. Используются сети и для графической иллюстрации системы отношений базы данных.
Широко применяются сети для графического изображения различных логических схем в теории автоматов, например схемы с памятью, у которых каждый узел F(i) — функция алгебры логики (см., например, рис. 4.17, 4.18).
Для формального описания совокупности процессов, протекающих одновременно, используют сети Петри. Они представляют собой ориентированные графы, состоящие из вершин двух видов: некоторых позиций и переходов, причем позиции изображают кружочками, а переходы — «планками» (рис. 2.22). Сети Петри предназначены для описания действия дискретных процессов во времени. Такие сети дают возможность моделировать ситуации протекания параллельных процессов, прослеживать возможные варианты их взаимодействия, выявлять нежелательные ситуации. Также в виде сетей изображаются схемы устройств, например радиоприемника или телевизора.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: