Сетевая модель график критический путь

Критический путь

Путь – любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующий за ней работы.
Полный путь L – любой путь, начало которого совпадает с исходным событием сети, а конец – с завершающим.
Наиболее продолжительный полный путь в сетевом графике называется критическим. Критическими также называются работы и события расположенные на этом пути. Работы этого пути определяют общий цикл завершения всего комплекса работ, планируемых при помощи сетевого графика. И для сокращения продолжительности проекта необходимо в первую очередь сокращать продолжительность работ, лежащих на критическом пути.

1. Составить экономическое содержание задачи и перечислить перечень работ.
2. Построить сетевой график и определить критический путь.
3. Рассчитать параметры сетевого графика и поздние сроки поступления событий, резервы времени.

Работа (i,j)	Количество предшествующих работ	Продолжительность tij	Ранние сроки: начало tij Р.Н.	Ранние сроки: окончание tij Р.О.	Поздние сроки: начало tij П.Н.	Поздние сроки:окончание tij П.О.	Резервы времени: полный tij П	Резервы времени: свободный tij С.В.	Резервы времени: событий Rj
(1,2)	0	3	0	3	1	4	1	0	1
(1,3)	0	6	0	6	0	6	0	0	0
(1,4)	0	4	0	4	9	13	9	9	0
(2,3)	1	2	3	5	4	6	1	1	0
(2,5)	1	5	3	8	12	17	9	2	7
(3,4)	2	7	6	13	6	13	0	0	0
(3,5)	2	4	6	10	13	17	7	0	7
(3,6)	2	4	6	10	15	19	9	9	0
(4,6)	2	6	13	19	13	19	0	0	0
(5,6)	2	2	10	12	17	19	7	7	0

Критический путь: (1,3)(3,4)(4,6)
Продолжительность критического пути: 19 Перейти к онлайн решению своей задачи Пример . Рассчитать параметры сетевого графика мероприятия по совершенствованию системы управления. Сетевая модель задана таблично. Продолжительность выполнения работ дана в виде минимальной и максимальной оценок. Требуется вычислить табличным методом все основные характеристики работ и событий, найти критический путь и его продолжительность.
Скачать

Источник

4.Сетевой график и его назначение. Полный путь. Критический путь.

Сетевой график — это графическая модель некоторого комплекса взаимосвязанных работ (проекта или производственного процесса).

Дугам графа соответствуют работы, т.е. отдельные операции проекта (дуга на графике изображается стрелкой). Работа имеет продолжительность и может требовать ресурсов. Над дугой может быть указана числовая характеристика работы (например, время ее выполнения).

Вершинам графа соответствуют события (вершина изображается кружком или квадратиком). Событие означает факт окончания всех работ, в него входящих, и начала всех работ, из него исходящих. Пока не выполнены все работы, входящие в событие, не может свершиться само событие и, следовательно, не может быть начата ни одна из работ, выходящих из него. Событие не имеет продолжительности и не требует ресурсов.

Полный путь – это цепочка следующих друг за другом работ, соединяющих исходное и завершающее событие. В примере можно выделить следующие полные пути (они обозначаются номерами событий, через которые проходят):

Критическим называется полный путь, имеющий наибольшую продолжительность во времени. Критических путей на сетевом графике может быть несколько (при этом все они имеют одинаковую продолжительность).

Продолжительность критического пути определяет критический срок проекта tкр. Все остальные (некритические) полные пути выполняются параллельно с критическим путем (цепочкой работ) и завершаются раньше. Критический срок, таким образом, показывает, за какое минимальное время может быть завершен весь проект. Очевидно, что увеличение сроков выполнения проекта больше tкр невыгодно.

Работы, принадлежащие критическому пути, называются критическими. Они не имеют резервов времени. Их несвоевременное выполнение ведет к срыву сроков всего проекта.

В нашем примере определить критический путь легко: нужно перебрать все возможные полные пути, рассчитать продолжительность каждого из них и выбрать наибольший:

Критическим является полный путь μ2, т.к. он имеет наибольшую продолжительность. Критический путь принято выделять на графике жирной линией (рис.2.3.).

Однако, если сетевой график достаточно сложный, перебрать все возможные пути затруднительно. Поэтому используют более формальный подход:

Для каждого события рассчитывают ранний и поздний сроки свершения.

На их основе определяют резервы времени всех событий и работ.

Проводят критический путь по тем работам и событиям, которые не имеют резерва времени.

5 Параметры событий сетевого графика. Параметры работ.

Ранний срок свершения события – это самый ранний момент, к которому завершаются все работы, предшествующие этому событию.

Ранний срок свершения события рассчитывается последовательно для каждого события от исходного к завершающему по следующим формулам:

, т.е. начало проекта принимается за нулевой момент времени;

, если событию j предшествует только одна работа;

, если событию предшествует несколько работ.

Здесь ij – множество работ, заканчивающихся j-м событием (дуги, входящие в вершину j);

–ранний срок свершения события, с которого начинается работа (i,j);

–продолжительность работы (i,j).

Резерв времени события показывает, на какой предельно допустимый срок может задержаться свершение события без нарушения критического срока проекта:

Полный резерв времени работы показывает, на сколько можно увеличить время выполнения этой работы при условии, что срок выполнения всего комплекса работ не изменится.

Резервы работ определяются на основе параметров свершения событий по следующей формуле:

Критические работы резервов времени не имеют, т.е. еще раз убеждаемся в том, что критический путь мы выделили правильно.

Резервы времени работ рассчитываются для организации контроля над выполнением проекта. Кроме того, зная эти резервы, можно оптимизировать срок выполнения проекта. Например, можно забрать ресурсы у тех работ, которые имеют резерв времени (снять часть рабочих с этих работ или урезать их финансирование) и передать их работам, лежащим на критическом пути. Тогда критические работы смогут быть выполнены раньше, что повлечет уменьшение критического срока всего проекта. Поскольку при таком перераспределении ресурсов критический путь может измениться, задача оптимизации критического срока является многоэтапной и может быть решена с использованием компьютера.

Источник

Порядок и правила построения сетевых графиков

Сетевые графики составляются на начальном этапе планирования. Вначале планируемый процесс разбивается на отдельные работы, составляется перечень работ и событий, придумываются их логические связи и последовательность выполнения, работы закрепляются за ответственными исполнителями. С их помощью оценивается длительность каждой работы. Затем составляется (сшивается) сетевой график. После упорядочения сетевого графика рассчитываются параметры событий и работ, определяются резервы времени и критический путь. Проводят анализ и оптимизация сетевого графика, который при необходимости вычерчивается заново с пересчетом параметров событий и работ.

При построении сетевого графика необходимо соблюдать ряд правил:

1) все стрелки сетевого графика имеют общее направление (слева направо);

2) между парой событий может быть изображена только одна работа;

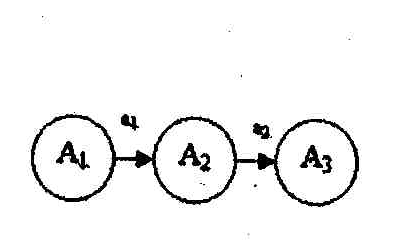
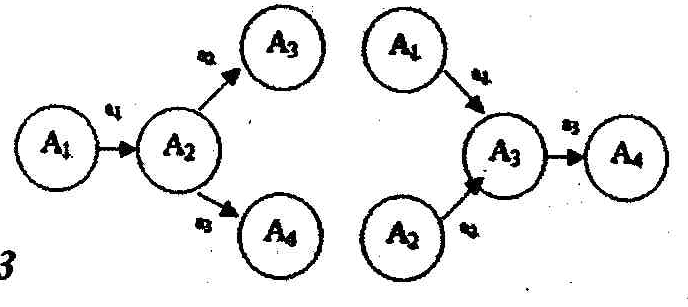
3) используются возможные варианты следования событий и работ (табличная запись и пути перехода приведены на рис. 1);

4) в сетевой модели не должно быть «тупиковых» событий, то есть событий, из которых не выходит ни одна работа, за исключением завершающего события;

5) в сетевом графике не должно быть «хвостовых» событий (кроме исходного), которым не предшествует хотя бы одна работа;

6) все события, кроме исходного и завершающего, должны иметь как входящие, так и выходящие стрелки;

7) если две работы начинаются в одно и то же время, в одном событии и оканчиваются в другом событии, то вводят фиктивное событие и фиктивную работу. При этом одна из параллельных работ замыкается на это фиктивное событие. Фиктивные работы имеют нулевую продолжительность и изображаются на графике пунктирными линиями;

8) в сети не должно быть замкнутых контуров и петель, то есть путей, соединяющих некоторые события с ними же самими.

Упорядочение сетевого графика. Понятие о пути

Предположим, что при составлении некоторого проекта выделено 12 событий – 0,1,2,3,4,5,6,7,8,9,10,11 и 24 связывающие их работы – (0,1), (0,2), (0,3), (1,2), (1,4), (1,5), (2,3), (2,5), (2,7), (3,6), (3,7), (3,10), (4,8), (5,8), (5,7), (6,10), (7,6), (7,8), (7,9), (7,10), (8,9), (9,11), (10,9), (10,11). Необходимо составить и упорядочить сетевой график.

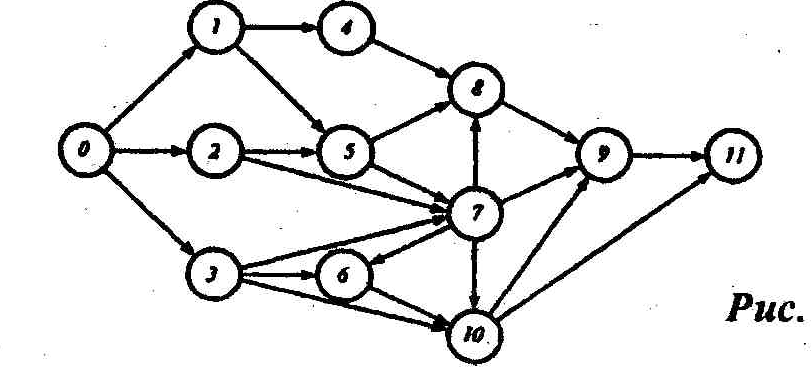
Как следует из перечня работ, исходным событием является событие 0 (ему не предшествуют никакие работы), а завершающим – событие 11 (за ним не следует ни одна работа). Полагая на сетевых графиках изменении времени слева направо, поместим событие 0 в левую часть графика, а событие 11 – в правую часть, разместив между ними промежуточные события в некотором порядке, соответствующем их номерам (рисунок 2). События свяжем работами-стрелками в соответствии с перечнем работ.

Упорядочение сетевого графика заключается в таком расположении событий и работ, при котором для любой работы предшествующее ей событие расположено левее и имеет меньший номер по сравнению с завершающим эту работу событием. Другими словами, в упорядоченном сетевом графике: от событий с меньшими номерами к событиям с большими номерами (рисунок 3).

Одно из важнейших понятий сетевого графика – понятие пути.

Путь – любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы.

Среди различных путей сетевого графика наибольший интерес представляет полный путь L – любой путь, начало которого совпадает с исходным событием сети, а конец – с завершающим.

Наиболее продолжительный полный путь в сетевом графике называется критическим. Критическими называются также работы и события, расположенные на этом пути.

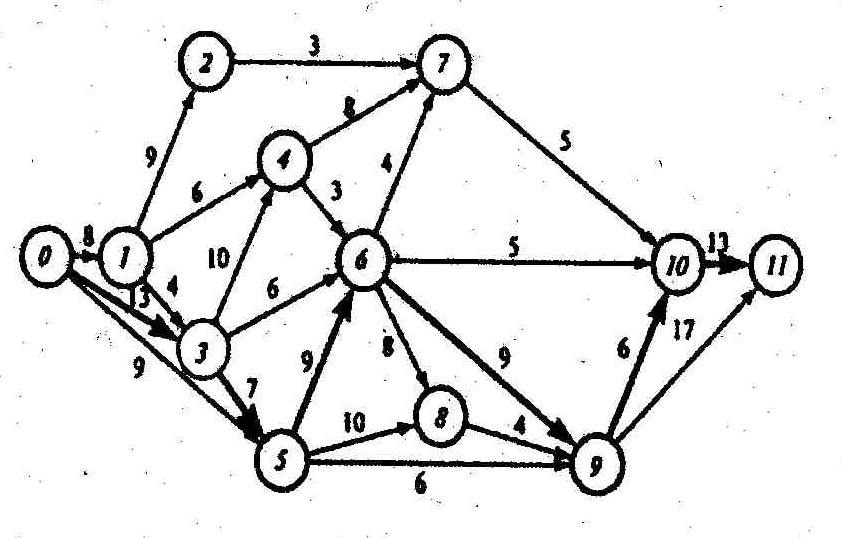
Например, для рассматриваемого нами сетевого графика (рисунок 3) полными путями будут: путь 0→1→2→7→10→11 продолжительностью 8+9+3+5+13=38 суток, путь 0→1→3→4→6→10→11 продолжительностью 8+4+10+3+5+13=43 суток, путь 0→3→5→6→9→10→11 продолжительностью 13+7+9+13+6+13=61 суток и т.д.

Последний путь имеет наибольшую продолжительность (не только среди приведенных четырех полных путей, но и среди всех полных путей, которых в данном случае насчитывается 64), поэтому он и является критическом. Продолжительность критического пути составляет 61 сутки, то есть для проведения комплекса работ понадобятся 61 сутки. Быстрее комплекс выполнить нельзя, так как для достижения завершающего события критический путь надо пройти обязательно.

Для достижения события 11 надо выполнить работу (10,11), то есть достичь события 10; для достижения события 10 надо провести работу (9,10), то есть достичь события 9; для достижения события 9 надо достичь работу (6,9), то есть достичь события 6, и т.д.

Определив критический путь, установили критические события сети 0,3,5,6,9,10,11 и критические работы (0,3), (3,5), (5,6), (6,9), (9,10), (10,11).

Критический путь имеет особое значение в системе СПУ, так как работы этого пути определяют общий цикл завершения всего комплекса работ, планируемых при помощи сетевого графика. И для сокращения продолжительность проекта необходимо в первую очередь сокращать продолжительность работ, лежащих на критическом пути.

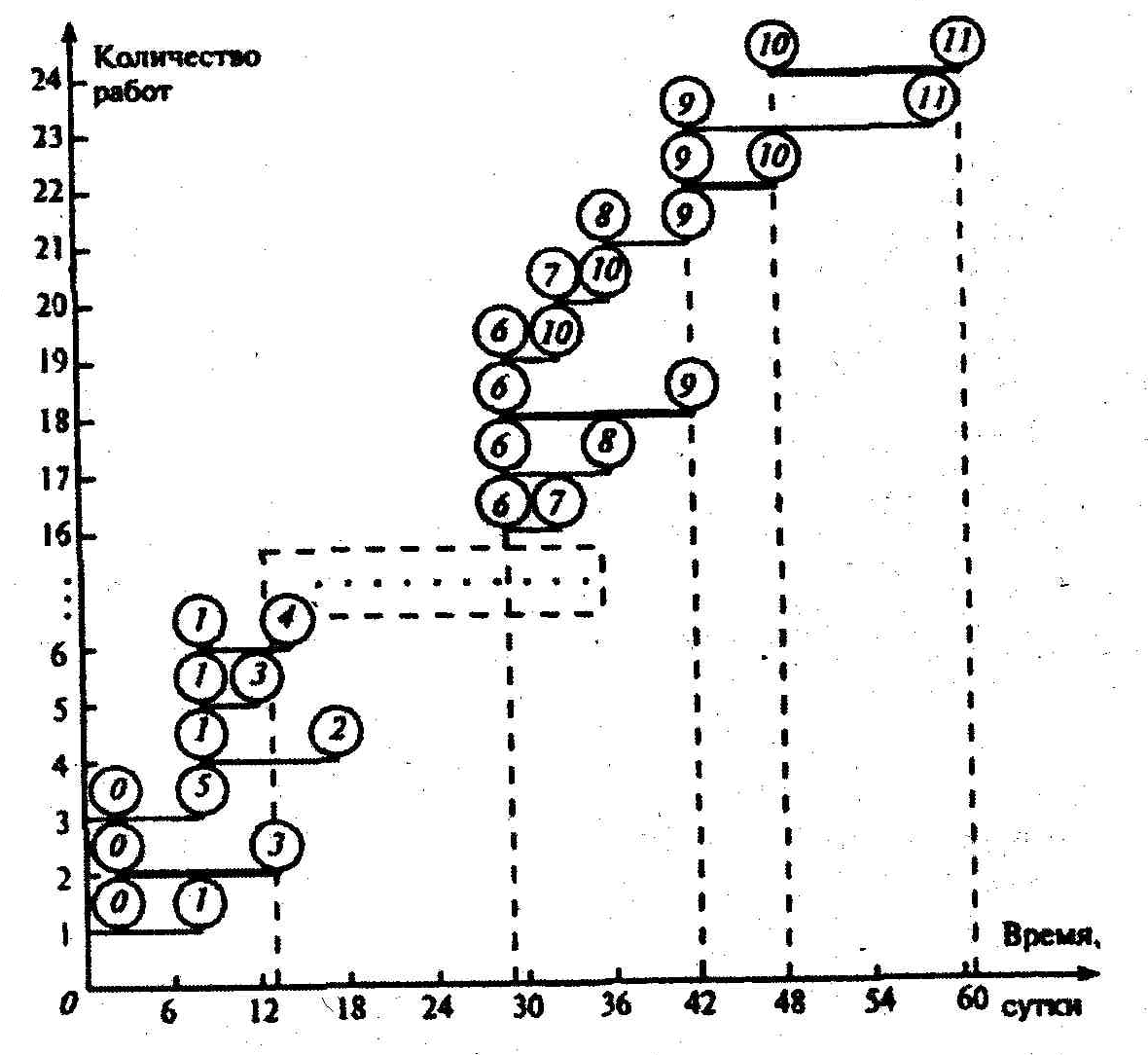
Классический вид сетевого графика – сеть, вычерченная без масштаба времени. Поэтому сетевой график, хотя дает четкое представление о порядке следования работ, но недостаточно нагляден для определения тех работ, которые должны выполняться в каждый данный момент времени. В связи с этим небольшой проект после упорядочения сетевого графика рекомендуется дополнить линейной диаграммой проекта. Такая линейная диаграмма для рассматриваемой сети показана на рисунке 4.

При построении линейной диаграммы каждая работа изображается параллельным оси времени отрезком, длина которого равна продолжительности этой работы. При наличии фиктивной работы нулевой продолжительности (в рассматриваемой сети ее нет) она изображается точкой. События i и j , начало и конец работы (i, j) помещают соответственно в начале и конце отрезка. Отрезки располагают один над другим, снизу вверх в порядке возрастания индекса i , а при одном и том же i – в порядке возрастания индекса j (на рисунке 4 вследствие ограниченности места не показаны работы-отрезки, выходящие из 2-, 3-, 4- и 5-го событий).

По линейной диаграмме проекта можно определить коритическое время, критический путь, а также резервы времени всех работ.

Критическое время комплекса работ равно координате на оси времени самого правого конца всех отрезков диаграммы:

Т_КР=t(11) =61 суток

Для определения критического пути рассматриваются работы-отрезки, конечные события которых совпадают с завершающим событием сети (в примере (9,11) и (10,11). Затем находят отрезок (9,10), правый конец которого лежит на одной вертикали (10) с левым концом одного из рассматриваемых ранее отрезков (10,11). Аналогично определяют и другие работы-отрезки критического пути: (6,9),….(0,3) (на рис. 4 они все выделены жирным шрифтом).

Источник