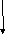Порядок и правила построения сетевых графиков
Сетевые графики составляются на начальном этапе планирования. Вначале планируемый процесс разбивается на отдельные работы, составляется перечень работ и событий, придумываются их логические связи и последовательность выполнения, работы закрепляются за ответственными исполнителями. С их помощью оценивается длительность каждой работы. Затем составляется (сшивается) сетевой график. После упорядочения сетевого графика рассчитываются параметры событий и работ, определяются резервы времени и критический путь. Проводят анализ и оптимизация сетевого графика, который при необходимости вычерчивается заново с пересчетом параметров событий и работ.
При построении сетевого графика необходимо соблюдать ряд правил:
1) все стрелки сетевого графика имеют общее направление (слева направо);
2) между парой событий может быть изображена только одна работа;
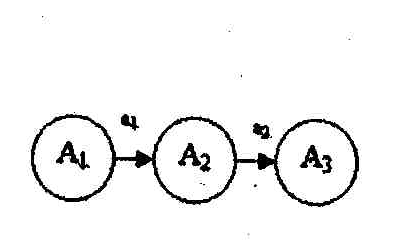
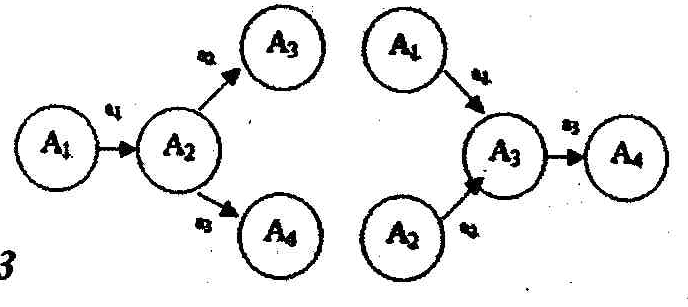
3) используются возможные варианты следования событий и работ (табличная запись и пути перехода приведены на рис. 1);
4) в сетевой модели не должно быть «тупиковых» событий, то есть событий, из которых не выходит ни одна работа, за исключением завершающего события;
5) в сетевом графике не должно быть «хвостовых» событий (кроме исходного), которым не предшествует хотя бы одна работа;
6) все события, кроме исходного и завершающего, должны иметь как входящие, так и выходящие стрелки;
7) если две работы начинаются в одно и то же время, в одном событии и оканчиваются в другом событии, то вводят фиктивное событие и фиктивную работу. При этом одна из параллельных работ замыкается на это фиктивное событие. Фиктивные работы имеют нулевую продолжительность и изображаются на графике пунктирными линиями;
8) в сети не должно быть замкнутых контуров и петель, то есть путей, соединяющих некоторые события с ними же самими.
Упорядочение сетевого графика. Понятие о пути
Предположим, что при составлении некоторого проекта выделено 12 событий – 0,1,2,3,4,5,6,7,8,9,10,11 и 24 связывающие их работы – (0,1), (0,2), (0,3), (1,2), (1,4), (1,5), (2,3), (2,5), (2,7), (3,6), (3,7), (3,10), (4,8), (5,8), (5,7), (6,10), (7,6), (7,8), (7,9), (7,10), (8,9), (9,11), (10,9), (10,11). Необходимо составить и упорядочить сетевой график.
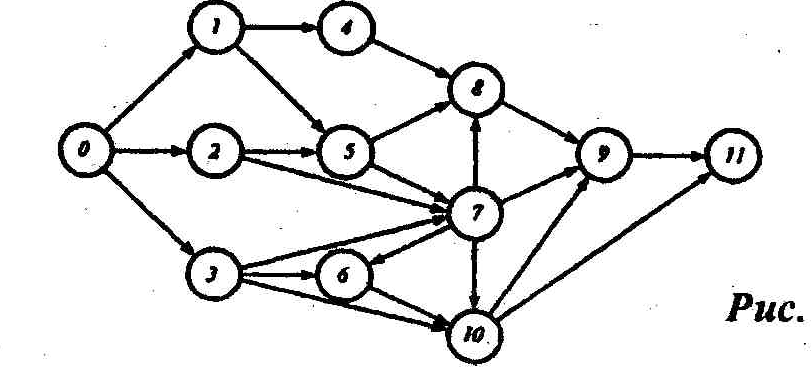
Как следует из перечня работ, исходным событием является событие 0 (ему не предшествуют никакие работы), а завершающим – событие 11 (за ним не следует ни одна работа). Полагая на сетевых графиках изменении времени слева направо, поместим событие 0 в левую часть графика, а событие 11 – в правую часть, разместив между ними промежуточные события в некотором порядке, соответствующем их номерам (рисунок 2). События свяжем работами-стрелками в соответствии с перечнем работ.
Упорядочение сетевого графика заключается в таком расположении событий и работ, при котором для любой работы предшествующее ей событие расположено левее и имеет меньший номер по сравнению с завершающим эту работу событием. Другими словами, в упорядоченном сетевом графике: от событий с меньшими номерами к событиям с большими номерами (рисунок 3).
Одно из важнейших понятий сетевого графика – понятие пути.
Путь – любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы.
Среди различных путей сетевого графика наибольший интерес представляет полный путь L – любой путь, начало которого совпадает с исходным событием сети, а конец – с завершающим.
Наиболее продолжительный полный путь в сетевом графике называется критическим. Критическими называются также работы и события, расположенные на этом пути.
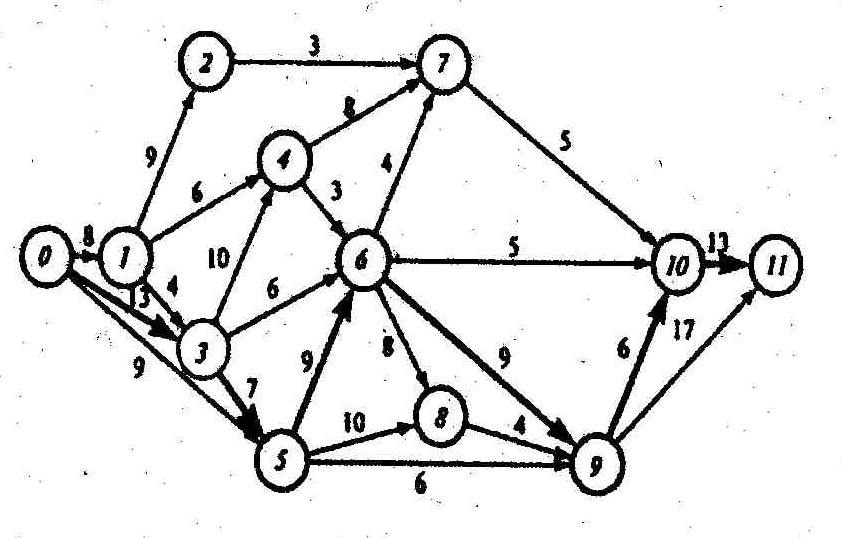
Например, для рассматриваемого нами сетевого графика (рисунок 3) полными путями будут: путь 0→1→2→7→10→11 продолжительностью 8+9+3+5+13=38 суток, путь 0→1→3→4→6→10→11 продолжительностью 8+4+10+3+5+13=43 суток, путь 0→3→5→6→9→10→11 продолжительностью 13+7+9+13+6+13=61 суток и т.д.
Последний путь имеет наибольшую продолжительность (не только среди приведенных четырех полных путей, но и среди всех полных путей, которых в данном случае насчитывается 64), поэтому он и является критическом. Продолжительность критического пути составляет 61 сутки, то есть для проведения комплекса работ понадобятся 61 сутки. Быстрее комплекс выполнить нельзя, так как для достижения завершающего события критический путь надо пройти обязательно.
Для достижения события 11 надо выполнить работу (10,11), то есть достичь события 10; для достижения события 10 надо провести работу (9,10), то есть достичь события 9; для достижения события 9 надо достичь работу (6,9), то есть достичь события 6, и т.д.
Определив критический путь, установили критические события сети 0,3,5,6,9,10,11 и критические работы (0,3), (3,5), (5,6), (6,9), (9,10), (10,11).
Критический путь имеет особое значение в системе СПУ, так как работы этого пути определяют общий цикл завершения всего комплекса работ, планируемых при помощи сетевого графика. И для сокращения продолжительность проекта необходимо в первую очередь сокращать продолжительность работ, лежащих на критическом пути.
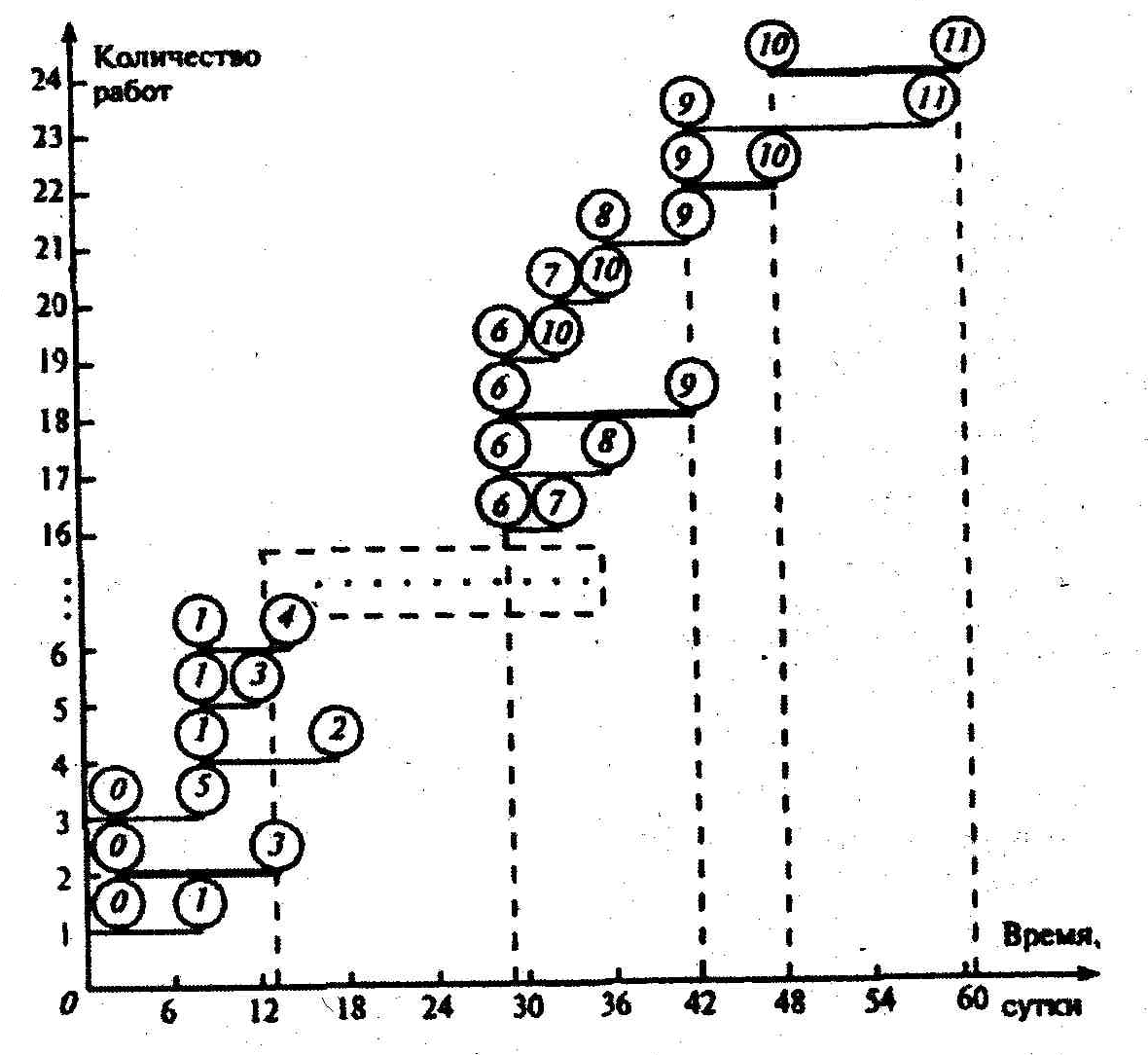
Классический вид сетевого графика – сеть, вычерченная без масштаба времени. Поэтому сетевой график, хотя дает четкое представление о порядке следования работ, но недостаточно нагляден для определения тех работ, которые должны выполняться в каждый данный момент времени. В связи с этим небольшой проект после упорядочения сетевого графика рекомендуется дополнить линейной диаграммой проекта. Такая линейная диаграмма для рассматриваемой сети показана на рисунке 4.
При построении линейной диаграммы каждая работа изображается параллельным оси времени отрезком, длина которого равна продолжительности этой работы. При наличии фиктивной работы нулевой продолжительности (в рассматриваемой сети ее нет) она изображается точкой. События i и j , начало и конец работы (i, j) помещают соответственно в начале и конце отрезка. Отрезки располагают один над другим, снизу вверх в порядке возрастания индекса i , а при одном и том же i – в порядке возрастания индекса j (на рисунке 4 вследствие ограниченности места не показаны работы-отрезки, выходящие из 2-, 3-, 4- и 5-го событий).
По линейной диаграмме проекта можно определить коритическое время, критический путь, а также резервы времени всех работ.
Критическое время комплекса работ равно координате на оси времени самого правого конца всех отрезков диаграммы:
ТКР=t(11) =61 суток
Для определения критического пути рассматриваются работы-отрезки, конечные события которых совпадают с завершающим событием сети (в примере (9,11) и (10,11). Затем находят отрезок (9,10), правый конец которого лежит на одной вертикали (10) с левым концом одного из рассматриваемых ранее отрезков (10,11). Аналогично определяют и другие работы-отрезки критического пути: (6,9),….(0,3) (на рис. 4 они все выделены жирным шрифтом).
9. Параметры, элементы и правила построения сетевых моделей, расчет сетевого графика (показать на примере).
начала одной или нескольких последующих работ(Рис. 2.3.).

Т – к – N рабочего времени, материальных ресурсов, затрат машинного времени.
— — — — — — — — — — — — — Технологическая зависимость — показывает зависимость начала выполнения каких либо последующих работ от окончания одной или нескольких предыдущих.
Позднее окончание работы (а),

—
Рис. 2.3. Схема обозначения основных элементов сетевой модели
Правила построения и расчета сетевой модели
- Направление стрелок следует принимать слева направо
- Форма модели и графика должна быть простой, без лишних пересечений, большинство работ следует изображать горизонтальными линиями
- При выполнении параллельных работ, т.е. если одно событие служит началом двух работ или более, заканчивающихся другим событием, вводится зависимость и дополнительное событие, иначе разные работы будут иметь одинаковый код.
- В графике не должно быть «тупиков», «хвостов» и «циклов». «Тупик» – событие (кроме завершающего), из которого не выходит ни одна работа. «Хвост» – событие (кроме исходного), в которое не входит ни одна работа. «Цикл» – замкнутый контур.
- Разрабатываемая сетевая модель строительства должна отражать абсолютно достоверно все особенности объекта, для чего предварительно необходимо изучить и проанализировать всю проектно-сметную документацию по объекту.
Сетевая модель и график могут разрабатываться в безразмерном (без масштабном) виде, то есть длина стрелок работ не соответствует значению продолжительности. Прежде чем приступать к расчету необходимо: -сетевую модель строительства объекта согласовать со всеми заинтересованными участниками строительства; -определить продолжительность выполнения каждой работы; -уточнить сроки строительства объекта по договору подряда. Параметры сетевого графика Параметры работ и сетевого графика: -номер события; -продолжительность выполнения работ; -раннее начало и раннее окончание работ; -позднее начало и позднее окончание работ; -частный резерв (запас) времени каждой работы; -общий резерв (запас) времени каждой работы; -длина критического пути (в днях) Расчет сетевого графика До начала выполнения расчета сетевого графика необходимо рассчитать продолжительность выполнения каждой работы сетевого графика. Расчет можно осуществлять графическим (секторным- непосредственно на графике) или табличным способом. Расчет графическим способом начинается с определения ранних сроков начала и окончания работ. Следующий шаг – расчет поздних сроков. Расчет поздних сроков осуществляется, начиная от последнего события. При правильном расчете поздних сроков в первом событии в левом и правом секторе должна быть цифра «0». Путь от первого события до последнего с наибольшим значением продолжительности и носит название «критический путь». Кроме этого следует учитывать то, что критический путь проходит через события, у которых в левом и правом секторе цифры одинаковые, а работы не имеют запасов времени. Критический путь – это самый длинный путь от исходного до завершающего события. Это и есть продолжительность строительства объекта. Работы, лежащие на критическом пути, называются критическими, другие работы являются не критическими и обладают запасами времени – частным и общим. На графиках критический путь выделяется двойной или просто более жирной линией. Возможность определения запасов времени по некритическим работам и использования их при корректировке графиков по различным критериям – это главное отличие и достоинство сетевого моделирования по сравнению с линейными графиками и циклограммами. Следующий шаг — расчет запасов времени – частного и общего. Частный резерв времени ( r) – это количество дней, на которое рассматриваемую работу можно растянуть или передвинуть без изменения ее продолжительности, не изменяя раннее начало последующей работы. Общий резерв времени (R) – это количество дней, на которое рассматриваемую работу можно растянуть или передвинуть без изменения ее продолжительности, не изменяя длины критического пути (продолжительности строительства объекта). Рассчитанный сетевой график приведен на рисунке После завершения расчетов необходимо построить график в масштабе времени и оценить его на предмет соответствия определенным критериям оптимальности.