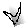1. Сетевая модель и ее основные элементы.
Сетевая модель представляет собой план выполнения некоторого комплекса взаимосвязанных работ (операций), заданного в специфической форме сети, графическое изображение которой, называется сетевым графиком.
Существуют различные типы сетевых графиков (СГ), но наиболее широкое применение получили так называемые вершины и стрелочные графы.
Основными элементами стрелочного графика являются «работа» («операция») и «событие».
1) действительными – процесс, требующий затрат времени и ресурсов;
2) фиктивными – логическая связь между двумя или несколькими работами (событиями), не требующая затрат времени и ресурсов.
Событие – это момент времени, определяющий возможность осуществления начала или окончания данной работы или несколько работ.
2. Построение сетевого графика, отражающего последовательность выполнения операций. Упорядочение событий сетевого графика.
На основе данных таблицы 1.1, отражающих последовательность выполнения операций построим стрелочный сетевой граф.
Под упорядочением событий итогового графа подразумевается нумерация, при которой для любой операции (работы) предшествующее ей событие расположено левее и имеет меньший номер по сравнению с завершающим эту работу событием.
В результате подобной нумерации событий каждая операция получает код (i-j), где i – номер предшествующего операции события, j – номер последующего события.
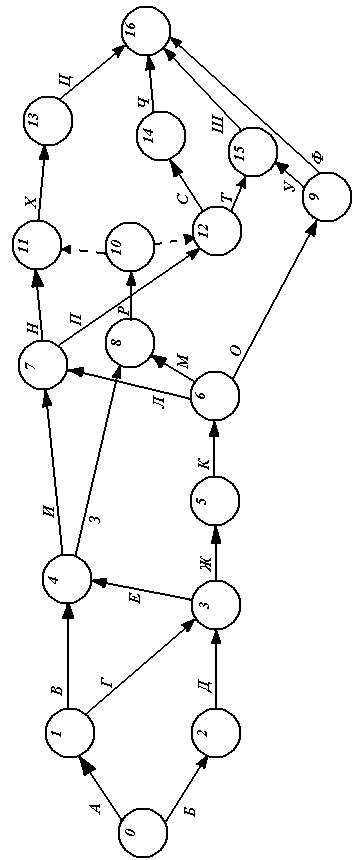
Упорядоченный сетевой график представлен на рисунке 2. 1.
Рис. 2.1. Упорядоченный сетевой график
3. Время выполнения операций.
После того как структура сети точно установлена и изображена графически, необходимо получить оценки продолжительности каждой операции.
Среднее значение – ожидаемая продолжительность операции:
где t0(i—j) – оптимистическая оценка – минимально возможный период, в течение которого может быть выполнена данная операция (продолжительность операции при самых благоприятных условиях);
tнв (i—j) – наиболее вероятная оценка – наилучшая оценка периода времени, в течение которого может быть выполнена данная операция.
tn(i—j) – пессимистическая оценка – максимально возможный период времени, в течение которого может быть выполнена данная операция.
Результаты расчетов, произведенных по формулам, по всем операциям сетевого графа, приведены в таблице 3.1.
Срок выполнения операции, недель
1. Элементы построения сетевых моделей
В основе метода сетевого планирования и управления (СПУ) лежит построение графика, по своему виду напоминающего сеть (переплетение нитей и узелков), поэтому график и получил название сетевого.
Сетевой моделью называется отображение процессов, выполнение которых подчинено достижению одной или нескольких целей, с указанием взаимосвязей между этими процессами.
Сетевым графиком называется график производства работ с установленными расчётом сроками их выполнения. Сетевой график представляет собой графическое изображение сетевой модели с рассчитанными параметрами.
Элементами сетевой модели являются работа, событие и путь:
а) работа – это трудовой процесс, требующий затрат времени и ресурсов.
Название работы является минимальной информацией о работе, содержащейся в сетевой модели (например, отрывка котлована, возведение каркаса, устройство кровли, поставка оборудования и т.д.).
Работа на графике изображается сплошной стрелкой, направленной слева направо с указанием над стрелкой продолжительности работы.
Работа, которая требует лишь затрат времени, называется работа – ожидание. Ожидание на графике изображается пунктирной стрелкой с указанием над стрелкой её продолжительности (например, процесс твердения бетона или ожидание поставки материалов). Эти работы требуют только затрат времени.
Для отображения правильной технологической последовательности между работами применяется зависимость. Ни времени, ни ресурсов «зависимость» не требует. На графике зависимость изображают пунктирной стрелкой, продолжительность которой равна нулю. В литературных источниках зависимость называют фиктивной работой.
Итак, понятие «работа» может иметь три значения:
работа
работа – ожидание
зависимость
б) событие – это итог какой-нибудь деятельности (работы), происходящей мгновенно. Любая работа начинается и заканчивается событием.
Событие не потребляет ни времени, ни трудовых ресурсов, оно обозначает только факт начала и окончания одной или нескольких работ. Событие графически обозначается кружком, внутри которого ставится его номер, или может обозначаться буквами.
Событие, не имеющее непосредственно предшествующих работ, называется исходным, не имеющее непосредственно следующих работ – завершающим. Событие, не являющееся ни исходным, ни завершающим, называется промежуточным.
На рис. 1 событие 1 – исходное, событие 6 – завершающее, события 2, 3, 4, 5 – промежуточные.
Все работы комплекса по отношению друг к другу подразделяются на данную, предшест-вующую и последующую работы. Обозначение работ см. на рис. 2.
в) путь – это непрерывная технологическая последовательность работ от исходного события к завершающему.
На рис. 3 дан сетевой график из восьми работ, одной зависимости и шести событий. На графике можно выделить 7 путей:
1-й путь проходит по событиям 1, 2, 3, 4, 6;
2-й путь проходит по событиям 1, 3, 5, 6;
3-й путь проходит по событиям 1, 2, 4, 6;
4-й путь проходит по событиям 1, 2, 3, 5, 6;
5-й путь проходит по событиям 1, 2, 3, 4, 5, 6;
6-й путь проходит по событиям 1, 2, 4, 5, 6;
7-й путь проходит по событиям 1, 3, 4, 5, 6.
Зная продолжительность каждой работы tij , можно определить продолжительность любого пути сетевого графика.
Продолжительность пути определяется как сумма продолжительностей работ, составляющих этот путь:
Критический путь – это путь, имеющий максимальную продолжительность. Он определяет конечный срок строительства, это самый трудоемкий и неблагоприятный путь.
Подкритический путь – это путь, продолжительность которого близка к продолжительности критического пути.
На рис. 3 длина различных путей от исходного события до завершающего равна:
1-й путь Т1 = 5 + 10 + 14 + 9 = 38;
4-й путь Т4 = 5 + 10 + 2 + 3 = 20;
5-й путь Т5 = 5 + 10 + 0 + 3 = 32;
6-й путь Т6 = 5 + 7 + 0 + 3 = 15;
7-й путь Т7 = 12 + 14 + 0 + 3 = 29.
Первый путь имеет наибольшую продолжительность из всех путей, значит, он является критическим.
Критическим путь назван потому, что, во-первых, из всех путей сетевого графика только он определяет общую продолжительность строительства; во-вторых, он указывает на работы, которые являются ведущими для выполнения заданного комплекса работ. Работы, лежащие на критическом пути, называются критическими.
На рис. 3 критическими работами являются 1-2; 2-3; 3-4; 4-6.
На сетевом графике критический путь выделяют красной двойной или жирной линией.
В сетевом графике может быть несколько критических путей одинаковой продолжительности. Определение продолжительности (длины) критического пути и критических работ – одна из основных задач, решаемых в методе сетевого планирования и управления (СПУ).
Сетевая модель, ее основные элементы
Объектами исследования методами СПУ являются крупные народнохозяйственные комплексы, научные исследования, конструкторская и технологическая подготовка производства новых видов изделий, строительство, реконструкция экономических объектов, капитальный ремонт основных фондов.
СПУ представляет собой совокупность расчетных методов, организационных и контрольных мероприятий по планированию и управлению комплексом работ.
Система СПУ позволяет:
— формировать календарный план реализации комплекса работ;
— выявлять резервы времени, трудовые, материальные и стоимостные ресурсы;
— осуществлять управление комплексом работ с прогнозированием и предупреждением возможных срывов в ходе работ;
— повышать эффективность управления в целом при четком распределении ответственности между руководителями разных уровней и исполнителями работ.
Комплекс работ (комплекс операций, проект) – всякая задача, для выполнения которой осуществляют разнообразные работы. Например, строительство здания, сборка самолета.
1. Составление перечня работ проекта, определение их логических связей и последовательности выполнения, закрепление работ за ответственными исполнителями, оценивание длительностей работ.
2. Реализация проекта в виде сетевого графика.
3. Упорядочение сетевого графика, расчет параметров работ, определение резервов времени и критического пути.
4. Анализ и оптимизация сетевого графика.
5. Составление временного графика реализации проекта.
Сетевая модель, ее основные элементы
Основой СПУ является сетевая модель.
Сетевой моделью называется экономико-математическая модель, отражающая для реализации некоторого проекта комплекс работ и событий, а также их логические и технологические последовательности и связи. Анализ сетевой модели, представленной в графической или табличной форме, позволяет:
— четко выяснить взаимосвязи этапов реализации проекта;
— определить наиболее оптимальный порядок выполнения этих этапов (например, для сокращения сроков выполнения всего комплекса работ).
Значит методы сетевого моделирования относятся к методам принятия оптимальных решений.
Математический аппарат сетевых моделей базируется на теории графов. Граф – это совокупность двух конечных множеств: множества точек, которые называются вершинами, и множества пар вершин, которые называются ребрами. Если рассматриваемые пары вершин являются упорядоченными, т.е. на каждом ребре задается направление, то граф называется ориентированным; в противном случае – неориентированным. Последовательность неповторяющихся ребер, ведущая от некоторой вершины к другой, образует путь. Граф называется связным, если для любых двух его вершин существует путь, их соединяющий; в противном случае граф называется несвязным. В экономике используются два вида графов: дерево и сеть. Дерево представляет собой связный граф без циклов, имеющий исходную вершину (корень) и крайние вершины; пути от исходной вершины к крайним вершинам называются ветвями. Сеть – это ориентированный конечный связный граф, имеющий начальную вершину (источник) и конечную вершину. Таким образом, сетевая модель представляет собой граф вида „ сеть”.
Сетевая модель в графическом изображении называется сетевым графиком. Ее отличительная особенность – четкое определение всех временных взаимосвязей предстоящих работ. Главные элементы сетевой модели – события и работы.
Термин работа используется в СПУ в широком смысле:
— это действительная работа – протяженный во времени процесс проекта, требующий затрат ресурсов (например, сборка изделия);
— это ожидание – протяженный во времени процесс, не требующий затрат труда (например, процесс сушки после покраски);
— это зависимость или фиктивная работа – логическая связь между двумя или несколькими работами (событиями), не требующими затрат труда, материальных ресурсов или времени. Эта связь указывает на тот факт, что возможность выполнения одной работы непосредственно зависит от результатов другой. Ее продолжительность принимается равной нулю (0).
Событие – это момент завершения какого-либо процесса, отражающий отдельный этап выполнения проекта. Событие устанавливает отношение предшествования среди процессов проекта. Оно может свершиться лишь тогда, когда закончатся все работы, ему предшествующие. Последующие работы могут начаться лишь тогда, когда событие свершится. Отсюда, двойственный характер события: для всех непосредственно предшествующих ему работ оно является конечным, а для всех непосредственно следующих за ним – начальным. При этом предполагается, что событие не имеет продолжительности и совершается как бы мгновенно.
В сетевой модели выделяют такие события:
— исходное – не имеет предшествующих работ и событий;
— завершающее – не имеет последующих работ и событий.
События на сетевом графике изображаются кружками (вершинами графа), а работы – стрелками (ориентированными дугами), указывающими связь между работами.
Принято под кодом (i,j) понимать работу, связывающую i -е событие с j -м событием. На рис. 4.1 показан фрагмент сетевого графика.
Рис. 4.1. Пример работ, события и кодирования работ
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: