Сетевая модель информационных систем

Сетевая модель данных

Сетевая модель данных — логическая модель данных, являющаяся расширением иерархического подхода, строгая математическая теория, описывающая структурный аспект, аспект целостности и аспект обработки данных в сетевых базах данных. Сетевая модель представляет собой структуру, у которой любой элемент может быть связан с любым другим элементом.Сетевая база данных состоит из наборов записей, которые связаны между собой так, что записи могут содержать явные ссылки на другие наборы записей. Тем самым наборы записей образуют сеть. Связи между записями могут быть произвольными, и эти связи явно присутствуют и хранятся в базе данных.

Особенности сетевой модели данных.

• Связи в сетевой модели данных осуществляются наборами, которые реализуются с помощью указателей. Сетевая модель данных являются особым витком в развитии иерархической модели данных, их основным отличием является то, что в сетевых моделях данных имеются указатели в обоих направлениях, которые соединяют родственную информацию.
• Сетевая модель данных предполагает наличие в ней произвольного количества записей и наборов в том числе их различных типов.
• Связь между двумя записями может выражаться произвольным количеством наборов.
• В любом наборе может быть только один владелец.
• Тип записи может быть владельцем в одних типах наборов и членом в других типах наборов, а также не входить ни в какой тип наборов.
• Допускается добавление новой записи в качестве экземпляра владельца, если экземпляр-член отсутствует.
• При удалении записи-владельца удаляются соответствующие указатели на экземпляры-члены, но сами записи-члены не уничтожаются (сингулярный набор).

Управление сетевыми данными.

Операции с сетевыми данными можно разделить на две группы: навигационные операции с данными и операции модификации данных.

Навигационные операции с данными

Навигационные операции сетевых баз данных осуществляют переход по связям, определенных в схеме баз данных, в результате таких переходов определяется запись, которую называют текущей.

• Найти конкретную запись в наборе однотипных записей и сделать ее текущей;
• Перейти от записи-владельца к записи-члену в некотором наборе;
• Перейти к следующей записи в некоторой связи;
• Перейти от записи-члена к владельцу по некоторой связи.

Операции модификации данных

Операций модификации сетевых баз данных осуществляют добавление новых записей данных, добавление новых наборов данных, удаление записей данных и наборов записей, модификация агрегатов и элементов данных.

• извлечь текущую запись в буфер прикладной программы для обработки;
• заменить в извлеченной записи значения указанных элементов данных на заданные новые их значения;
• запомнить запись из буфера в БД;
• создать новую запись;
• уничтожить запись;
• включить текущую запись в текущий экземпляр набора;
• исключить текущую запись из текущего экземпляра набора.

Реляционная модель данных

Реляционная модель — совокупность данных, состоящая из набора двумерных таблиц. В теории множеств таблице соответствует термин отношение (relation), физическим представлением которого является таблица, отсюда и название модели – реляционная. Соответственно теория построения баз данных, которая является приложением к задачам обработки данных таких разделов математики, как теория множеств и логика первого порядка. В сравнении с иерархической и сетевой моделью данных, реляционная модель отличается более высоким уровнем абстракции данных. Реляционная модель является удобной и наиболее привычной формой представления данных, так в настоящее время эта модель является фактическим стандартом, на который ориентируются практически все современные коммерческие СУБД. На реляционной модели данных строятся реляционные базы данных.

При табличной организации данных отсутствует иерархия элементов. Строки и столбцы могут быть просмотрены в любом порядке, поэтому высока гибкость выбора любого подмножества элементов в строках и столбцах. Любая таблица в реляционной базе состоит из строк, которые называют записями, и столбцов, которые называют полями. На пересечении строк и столбцов находятся конкретные значения данных. Для каждого поля определяется множество его значений.

В реляционной модели данных применяются разделы реляционной алгебры, откуда и была заимствована соответствующая терминология.В реляционной алгебре поименованный столбец отношения называется атрибутом, а множество всех возможных значений конкретного атрибута – доменом. Строки таблицы со значениями разных атрибутов называют кортежами. Атрибут, значение которого однозначно идентифицирует кортежи, называется ключевым (или просто ключом). Так ключевое поле – это такое поле, значения которого в данной таблице не повторяется. В отличие от иерархической и сетевой моделей данных в реляционной отсутствует понятие группового отношения. Для отражения ассоциаций между кортежами разных отношений используется дублирование их ключей. Сложный ключ выбирается в тех случаях, когда ни одно поле таблицы однозначно не определяет запись.

Записи в таблице хранятся упорядоченными по ключу. Ключ может быть простым, состоящим из одного поля, и сложным, состоящим из нескольких полей. Сложный ключ выбирается в тех случаях, когда ни одно поле таблицы однозначно не определяет запись.

Кроме первичного ключа в таблице могут быть вторичные ключи, называемые еще внешними ключами, или индексами. Индекс – это поле или совокупность полей, чьи значения имеются в нескольких таблицах и которое является первичным ключом в одной из них. Значения индекса могут повторяться в некоторой таблице. Индекс обеспечивает логическую последовательность записей в таблице, а также прямой доступ к записи.

По первичному ключу всегда отыскивается только одна строка, а по вторичному – может отыскиваться группа строк с одинаковыми значениями первичного ключа. Ключи нужны для однозначной идентификации и упорядочения записей таблицы, а индексы для упорядочения и ускорения поиска.

Индексы можно создавать и удалять, оставляя неизменным содержание записей реляционной таблицы. Количество индексов, имена индексов, соответствие индексов полям таблицы определяется при создании схемы таблицы.

Индексы позволяют эффективно реализовать поиск и обработку данных, формируя дополнительные индексные файлы. При корректировке данных автоматически упорядочиваются индексы, изменяется местоположение каждого индекса согласно принятому условию (возрастанию или убыванию значений). Сами же записи реляционной таблицы не перемещаются при удалении или включении новых экземпляров записей, изменении значений их ключевых полей.

С помощью индексов и ключей устанавливаются связи между таблицами. Связь устанавливается путем присвоения значений внешнего ключа одной таблицы значениям первичного ключа другой. Группа связанных таблиц называется схемой данных. Информация о таблицах, их полях, ключах и т.п. называется метаданными.

• Изложение информации в простой и понятной для пользователя форме (таблица).
• Реляционная модель данных основана на строгом математическом аппарате, что позволяет лаконично описывать необходимые операции над данными.
• Независимость данных от изменения в прикладной программе при изменении.
• Позволяет создавать языки манипулирования данными не процедурного типа.
• Для работы с моделью данных нет необходимости полностью знать организацию БД.

• Относительно медленный доступ к данным.
• Трудность в создании БД основанной на реляционной модели.
• Трудность в переводе в таблицу сложных отношений.
• Требуется относительно большой объем памяти.

Источник

3)Сетевые информационные модели

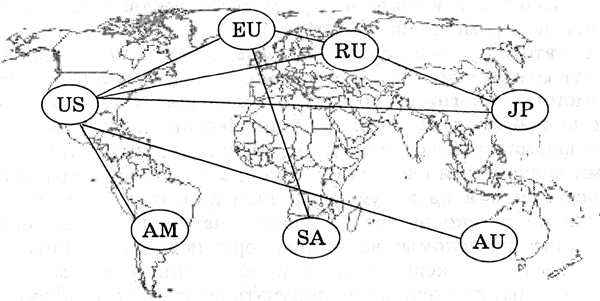
Сетевые информационные модели применяются для отражения систем со сложной структурой, в которых связи между элементами имеют произвольный характер.

Например, различные региональные части глобальной компьютерной сети Интернет (американская, европейская, российская, австралийская и так далее) связаны между собой высокоскоростными линиями связи. При этом одни части (например, американская) имеют прямые связи со всеми региональными частями Интернета, а другие могут обмениваться информацией между собой только через американскую часть (например, российская и австралийская).

Построим граф, который отражает структуру глобальной сети Интернет (рис. 2.7). Вершинами графа являются региональные сети. Связи между вершинами носят двусторонний характер и поэтому изображаются ненаправленными линиями (ребрами), а сам граф поэтому называется неориентированным.

Представленная сетевая информационная модель является статической моделью. С помощью сетевой динамической модели можно, например, описать процесс передачи мяча между игроками в коллективной игре (футболе, баскетболе и так далее).

1) Алгоритм — набор инструкций, описывающих порядок действий исполнителя для достижения результата решения задачи за конечное время. В старой трактовке вместо слова «порядок» использовалось слово «последовательность», но по мере развития параллельности в работе компьютеров слово «последовательность» стали заменять более общим словом «порядок». Это связано с тем, что работа каких-то инструкций алгоритма может быть зависима от других инструкций или результатов их работы. Таким образом, некоторые инструкции должны выполняться строго после завершения работы инструкций, от которых они зависят. Независимые инструкции или инструкции, ставшие независимыми из-за завершения работы инструкций, от которых они зависят, могут выполняться в произвольном порядке, параллельно или одновременно, если это позволяют используемые процессор и операционная система.

Линейный (последовательный) алгоритм — описание действий, которые выполняются однократно в заданном порядке.

Линейными являются алгоритмы отпирания дверей, заваривания чая, приготовления одного бутерброда. Линейный алгоритм применяется при вычислении арифметического выражения, если в нем используются только действия сложения и вычитания.

Циклический алгоритм — описание действий, которые должны по вторяться указанное число раз или пока не выполнено заданное условие. Перечень повторяющихся действий называется телом цикла.

Многие процессы в окружающем мире основаны на многократном повторении одной и той же последовательности действий. Каждый год наступают весна, лето, осень и зима. Жизнь растений в течение года проходит одни и те же циклы. Подсчитывая число полных поворотов минутной или часовой стрелки, человек измеряет время.

Условие — выражение, находящееся между словом «если» и словом «то» и принимающее значение «истина» или «ложь».

Разветвляющийся алгоритм — алгоритм, в котором в зависимости от условия выполняется либо одна, либо другая последовательность действий.

Примеры разветвляющих алгоритмов: если пошел дождь, то надо открыть зонт; если болит горло, то прогулку следует отменить; если билет в кино стоит не больше десяти рублей, то купить билет и занять свое место в зале, иначе (если стоимость билета больше 10 руб.) вернуться домой.

В общем случае схема разветвляющего алгоритма будет выглядеть так: «если условие, то. иначе. ». Такое представление алгоритма получило название полной формы. Неполная форма, в которой действия пропускаются: «если условие, то. ».

Вспомогательный алгоритм — алгоритм, который можно использовать в других алгоритмах, указав только его имя. Например: вы в детстве учились суммировать единицы, затем десятки, чтобы суммировать двузначные числа содержащие единицы вы не учились новому методу суммирования, а воспользовались старыми методами.

Источник