Коэффициент напряженности работ.
Анализ сетевого графика начинается с анализа структуры сети, включающего контроль построения сетевого графика, устранение целесообразности выбора работ, степени их расчленения. Затем проводится классификация и группировка работ по выявлению резервов, с тем, чтобы определить степень трудности выполнения в срок каждой группы работ. Величина полного резерва времени не всегда может достаточно точно характеризовать, насколько напряженным является выполнение той или иной работы некритического пути. Все зависит от того, на какую последовательность работ распространяется вычисленный резерв, какова продолжительность этой последовательности. Определить степень трудности выполнения в срок каждой группы работ некритического пути можно с помощью коэффициента напряженности работ. Коэффициентом напряженностиКНработы(i,j) называют отношение продолжительности несовпадающих (заключенных между одними и теми же событиями) отрезков пути, одним из которых является путь максимальной продолжительности, проходящий через данную работу, а другим – критический путь: КН(i,j)=
(12) где: 
— продолжительность максимального пути, проходящего через работу (i, j); 
— продолжительность отрезка рассматриваемого пути, совпадающего с критическим путем; 
— продолжительность (длина) критического пути. Находим коэффициент напряженности работы (1;2): Максимальный путь, проходящий через работу (1;2) – это путь 0→1→2→10→11→12→13→14→15. Продолжительность: 1+1+2+3+3+30+10+5=55. Продолжительность отрезка пути, совпадающего с критическим путем: 3+3+30+10+5=51. Подставим найденные значения в формулу: Кн(1;2)= 
Находим коэффициент напряженности работы (3;6): Максимальный путь, проходящий через работу (3;6) – это путь 0→3→6→11→12→13→14→15. Продолжительность: 4+5+1+3+30+10+5=58. Продолжительность отрезка пути, совпадающего с критическим путем: 3+30+10+5=48. Подставим найденные значения в формулу: Кн(3;6)= 
Находим коэффициент напряженности работы (4;7): Максимальный путь, проходящий через работу (4;7) – это путь 0→4→7→9→12→13→14→15. Продолжительность: 3+2+5+2+30+10+5=57. Продолжительность отрезка пути, совпадающего с критическим путем: 30+10+5=45. Подставим найденные значения в формулу: Кн(4;7)= 
Коэффициент напряженности КН(i, j) может изменяться в пределах от 0 (для работ, у которых отрезки максимального из путей, не совпадающие с критическим путем, состоят из фиктивных работ нулевой продолжительности) до 1 (для работ критического пути). Чем ближе к 1 коэффициент напряженности, тем сложнее выполнять данную работу в установленные сроки, а чем ближе он к нулю, тем большим относительным резервом обладает максимальный путь, проходящий через данную работу. Работы могут обладать одинаковыми полными резервами, но разной степенью напряженности. И наоборот, различным полным резервам могут соответствовать одинаковые коэффициенты напряженности. Из формулы (13) видно, что величина коэффициента напряженности зависит от RП и 
. Чем полный резерв времени RП больше выполнения некоторой работы и 
, (то есть чем меньше
—
— отрезок времени максимального пути, проходящего через эту работу и не совпадающего с критическим путем), тем больше будет дробь, стоящая в правой части формулы (13), и тем меньше коэффициент напряженности этой работы, тем легче будет ее выполнить. В общем случае указанная дробь определяет удельный вес полных резервов времени работ в продолжительности отрезков максимальных путей, не совпадающих с критическим путем. Чем больше этот удельный вес, тем меньше коэффициент напряженности. Выделяют следующие зоны: -критическая: Кн(i;j)>0,8 -подкритическая: 0,60,8 (0,4) попадает в критическую зону, так как Кн(0,3)=0,9>0,8 (3,6) попадает в критическую зону, так как Кн(3,6)=0,9>0,8 (4,7) попадает в критическую зону, так как Кн(4.7)=0,9>0,8 (2,10) попадает в резервную зону, так как Кн(2,10)=0,50,8 (7,8) попадает в критическую зону, так как Кн(7,8)=0,9>0,8 (7,9) попадает в критическую зону, так как Кн(7,9)=0,9>0,8 (8,9) попадает в критическую зону, так как Кн(8,9)=0,9>0,8 (9,12) попадает в критическую зону, так как Кн(9,12)=0,9>0,8 ЗАКЛЮЧЕНИЕ: Искусство экономико-математического моделирования состоит в выполнении двух противоречивых между собой требований:
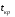
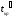
- с одной стороны, заменить сложный экономический объект его математической моделью для облегчения проводимых исследований;
- с другой стороны, обеспечить адекватность математической модели моделируемому экономическому объекту.
В данной курсовой работе был построен сетевой график по предприятию «ЗАО Авто-агрегат центр» г. Наб. Челны, проведен его анализ, и произведена оптимизация сетевого графика. Рациональность данных методик заключается в том, что они позволяют найти критический путь сетевого графика. При построении сетевого график был определен критический путь проекта, составляющий 59 дня. Произведено решение двух основных задач сетевого планирования: задачу анализа оптимальности уже готового сетевого графика и задачу его оптимизации по длительности. Заключение анализа сетевого графика состоит в том, чтобы выявить резервы времени работ, не лежащих на критическом пути, и направить их на работы, лимитирующие срок завершения комплекса работ. Результатом этого является сокращение продолжительности критического пути. Сетевое планирование при реализации сложных проектов увеличивает эффективность работ и способствует уменьшению затрат. Решение экономических задач с помощью метода математического моделирования позволяет осуществлять эффективное управление как отдельными производственными процессами на уровне прогнозирования и планирования экономических ситуаций и принятия на основе этого управленческих решений, так и всей экономикой в целом.
Для продолжения скачивания необходимо пройти капчу:
8. Коэффициент напряженности работы. Анализ и оптимизация сетевого графика
Прежде чем использовать сетевой график как основной инструмент управления ходом работ, необходимо провести его анализ и оптимизацию. Анализ и оптимизация сетевого графика в системах СПУ, в которых объектом планирования и контроля являются сроки выполнения работ (а именно такие графики мы и рассматриваем), в основном сводится к сокращению продолжительности критического пути.
Анализ сетевого графика выполняется с целью, во-первых, проверки правильности оценки времени критических работ и работ, имеющих минимальные резервы времени; во-вторых, сравнения установленного срока выполнения комплекса работ со сроком, полученным в результате расчета временных параметров сетевого графика. Главная цель анализа сети с временной оценкой работ состоит в определении наиболее целесообразных способов достижения оптимальных сроков выполнения комплекса работ.
Основное внимание в сетевом графике необходимо обращать на критические работы. Увеличение или уменьшение продолжительности критических работ, а, следовательно, и критического пути может привести к изменению срока завершения комплекса работ в целом. Для выполнения запланированного комплекса работ в заданный срок необходимо не только увязать этот срок с рассчитанным по сетевому графику (в случае, когда заданный срок оказался меньше расчетного, т.е. меньше ), с отпущенными материальными и трудовыми ресурсами, но и так организовать выполнение работ, чтобы составленный с помощью сетевого графика план стал реальностью.
Для оптимизации сетевой модели, выражающейся в перераспределении ресурсов с ненапряженных работ на критические для ускорения их выполнения, необходимо как можно более точно оценить степень трудности своевременного выполнения всех работ, а также «цепочек» пути. Более точным инструментом решения этой задачи по сравнению с полным резервом является коэффициент напряженности, который может быть вычислен одним из двух способов по формуле:
где — продолжительность максимального пути, проходящего через работу ; — продолжительность (длина) критического пути; — продолжительность отрезка рассматриваемого (максимального пути, проходящего через работу ) пути, совпадающего с критическим путем; — полный резерв времени работы
Коэффициент напряженности может изменяться в пределах от 0 (для работ, у которых отрезки максимального из путей, не совпадающие с критическим путем, состоят из фиктивных работ нулевой продолжительности) до 1 (для работ критического пути). Чем ближе к 1 коэффициент напряженности, тем сложнее выполнить данную работу в установленные сроки. Чем ближе коэффициент напряженности к 0, тем большим относительным резервом обладает максимальный путь, проходящий через данную работу.
На основе коэффициента напряженности все работы сетевого графика могут быть разделены на три группы:
В результате перераспределения ресурсов стараются максимально уменьшить общую продолжительность работ, что возможно при переводе всех работ в первую группу.
Оптимизация сетевого графика представляет процесс улучшения организации выполнения комплекса работ с учетом срока его выполнения. Оптимизация проводится с целью сокращения длины критического пути, выравнивания коэффициентов напряженности работ, рационального использования ресурсов.
В первую очередь принимаются меры по сокращению продолжительности работ, находящихся на критическом пути. Это достигается:
- перераспределением всех видов ресурсов, как временных (использование резервов времени некритических путей), так и трудовых, материальных, энергетических; при этом перераспределение ресурсов должно идти, как правило, из зон, менее напряженных, в зоны, объединяющие наиболее напряженные работы;
- сокращением трудоемкости критических работ за счет передачи части работ на другие пути, имеющие резервы времени;
- параллельным выполнением работ критического пути;
- пересмотром топологии сети, изменением состава работ и структуры сети.
В процессе сокращения продолжительности работ критический путь может измениться, и в дальнейшем процесс оптимизации будет направлен на сокращение продолжительности работ нового критического пути и так будет продолжаться до получения удовлетворительного результата. В идеале длина любого из полных путей может стать равной длине критического пути или по крайней мере пути критической зоны. Тогда все работы будут вестись с равным напряжением, а срок завершения проекта существенно сократится.
Для рис. 8 определить характеристики СПУ:
1) ранние и поздние сроки совершения событий;
2) резервы времени событий;
3) критический путь и его длину, пояснить смысл найденной величины (длина критического пути);
4) для некритических работ найти полные, свободные и независимые резервы времени;
5) для некритических работ найти коэффициенты напряженности и пояснить за счет каких работ возможна оптимизация сетевой модели.
7.6. Коэффициент напряженности работы. Анализ и оптимизация сетевого графика
Критический путь и резервы времени работ находятся для того, чтобы можно было выполнить анализ и оптимизацию сетевого графика. Вначале анализируется топология сети, т.е. все возможные пути, их направленность, целесообразность выбора работ, правильность их разбиения на отдельные участки.
После этого работы классифицируются и группируются по величине резерва. Необходимо отметить, что абсолютная величина резерва не всегда достаточно полно характеризует степень напряженности выполнения работы, нележащей на критическом пути. Для устранения этого недостатка используют коэффициент напряженности работы.
Коэффициент напряженности работы KH работы (i,j) вычисляется следующим образом:
где t(Lmax) — продолжительность максимального пути, проходящего через работу (i,j);
tkp — продолжительность критического пути;
t ’ kp— продолжительность отрезка рассматриваемого пути, совпадающего с критическим путем.
Коэффициент напряженности может меняться от 0 до 1.
Нулю коэффициент напряженности равен для тех работ, у которых отрезки максимального из путей, не совпадающие с критическим путем, состоят из фиктивных работ нулевой продолжительности. Для работ критического пути коэффициент напряженности равен 1.
Чем выше коэффициент напряженности, тем сложнее выполнить работу в установленные сроки.
В зависимости от величины коэффициента напряженности работы классифицируют по трем зонам:
7.7. Литература по теме 7
- Карасев А.И. и др. Математические методы и модели в планировании: Учебное пособие для экономических вузов/ А.И.Карасев, Н.Ш.Кремер, Т.И.Савельева: Под ред. А.И.Карасева. — М.: Экономика, 1987. — С.142-181.
- Ларионов А.И. и др. Экономико-математические методы в планировании / А.И. Ларионов, Т.И. Юрченко, А.Л. Новоселов. — 2-е изд., перераб. и доп. — М.: Высш. шк., 1991. — С.147-168.
- Пелих А.С., Терехов Л.Л., Кизилов А.Н. Методы анализа, планирования и управления: Учеб. пособие / РГЭА: Ростов н/Д, 1997. — С.217-228.
- Перепелицкий С.Н. Экономико-математические методы и модели в планировании и управлении на предприятиях лесной промышленности: Учеб. для вузов. — М.: Лесная пром-сть, 1989. — С.292-321.
- Спирин А.А., Фомин Г.П. Экономико-математические методы и модели в торговле: Учеб. пособие для экон. и товаровед. факультетов торг. вузов. — М.: Экономика, 1988. — С.108-129.