Сетевая модель наикратчайший путь

6.4.Представление сетевых задач как задач линейного программирования

Задачи о кратчайшем пути и максимальном потоке можно сформулировать как задачи линейного программирования. Следует, однако, подчеркнуть, что решение сетевых задач симпликс-методом едва ли целесообразно. С другой стороны, изучение формулировок сетевых задач как задач ЛП помогает идентифицировать модели ЛП, которые на первый взгляд не являются сетевыми, но которые либо непосредственно, либо с некоторыми модификациями можно свести к сетевым. Очевидное преимущество такого подхода состоит в том, что при использовании сетевых постановок эффективность вычислений может значительно увеличиться.

Модель линейного программирования для задачи о кратчайшем пути строится следующим образом.

Пусть x_ij представляет величину потока по дуге (i, j). Тогда задача о кратчайшем пути в сети с n узлами формулируется как

Ограничения модели линейного программирования соответствует формулировке задачи о кратчайшем пути как транспортной задачи с промежуточными пунктами, ранее рассмотренной. Единица потока доставляется из узла 1 в узел n. Первым и последним ограничениями устанавливается, что суммарный поток (сумма переменных), выходящий из узла 1, равен 1, как и суммарный поток, поступающий в узел n. В любом промежуточном узле суммарный входной поток равен суммарному выходному потоку. Целевая функция требует, чтобы общее расстояние, пройденное единицей потока, было минимальным.

Следует подчеркнуть, что данная постановка имеет реальный смысл, если x_ij = 0 или 1, т. е. дуга (i, j) принадлежит кратчайшему пути, только если x_ij = 1. Если x_ij = 0, то (i, j) не входит в кратчайший путь. Несмотря на то, что условия x_ij = 0 или 1 не отражены в модели в явном виде, её специальная структура всегда приводит к оптимальному решению, которое удовлетворяет этим требованиям. В самом деле, модель обладает свойством абсолютной унимодулярности, согласно которому в решении задачи линейного программирования всегда x_ij = 0 или 1 (сравните с моделью с прмежуточными пунктами).

Таким же образом к задаче линейного программирования можно свести задачу о максимальном потоке. Пусть y – поток из источника 1 в сток n. Обозначив поток в дуге (i, j) через x_ij, получим следующую модель линейного программирования:

Z = y max

где u_ij обозначает пропускную способность дуги (i, j). Заметим, что ограничения строятся по той же схеме, которая использовалась для построения модели ЛП задачи о кратчайшем пути.

Глава 7.Применение сетевых моделей в транспортировке грузов

7.1. Определение кратчайших расстояний между пунктами транспортной сети

Исходными данными для определения кратчайших расстояний является транспортная сеть, представленная на рис. 7.1. Воспользуемся методом потенциалов. Сущность его состоит в следующем:

1. Потенциал одной из вершин (назовем ее исходной, например, вершины А) принимают за 0, то есть Р_А=0.
2. Далее по формуле (7.1) определяются потенциалы всех вершин,непосредственносвязанных с ней.

Р_j = Р_i + ℓ_ij ,

где i,j – текущие индексы соответственно исходной и непосредственно связанной с ней вершин; Р_i – потенциал исходной вершины, км; Р_j – потенциал вершины, непосредственно связанной с исходной, км;

ℓ_ij – длина звена между исходной и непосредственно связанной с ней вершинами i и j, км.

1. Из всех рассчитанных таким образом потенциалов выбирается наименьший, его значение записывается в таблицу кратчайших расстояний, а соответствующее звено на рисунке отмечается стрелкой.
2. Вершина с наименьшим потенциалом принимается за исходную, от нее вновь определяются потенциалы всех вершин, непосредственно связанных с ней. Просматриваются все известные к этому моменту потенциалы (определенные как на предыдущем, так и на данном этапе), из них вновь выбирается наименьший, его значение заносится в эту же таблицу, а соответствующее звено на рисунке отмечается стрелкой. Таким образом, расчеты повторяются до полного заполнения таблицы и рисунка.

Кратчайшее расстояние между пунктами находим методом потенциалов. На данной транспортной сети (рис. 7.1) нет никаких ограничений по организации дорожного движения, то есть расстояние между пунктами А и И равно расстоянию между пунктами И и А. Таким образом, матрица кратчайших расстояний получается симметричной, поэтому в табл. 103 будем заполнять только верхнюю правую половину.

Рис. 7.17. Транспортная сеть

Полагаем Р_А = 0.

Вершина А непосредственно связана с вершинами: Д, Б, В. Найдем потенциалы этих вершин:

Из всех найденных потенциалов выбираем наименьший, им является потенциал вершины В. Р_В =2. Его значение заносим в матрицу кратчайших расстояний, соответствующее звено на рисунке отмечаем стрелкой.

Исходной принимаем вершину В, с которой связаны вершины Д, Б,Г, Е, З, Ж.

Из всех найденных потенциалов выбираем наименьший, им является потенциал вершины Д. Р_Д =3. Так как найден еще один потенциал вершины Д через вершину В и он оказался больше Р_Д =3, то его в дальнейших расчетах не рассматриваем. Значение выбранного потенциала заносим в матрицу кратчайших расстояний, соответствующее звено на рисунке отмечаем стрелкой.

С вершиной Д связаны вершины К, Е.

Из всех найденных потенциалов выбираем наименьший, им является потенциал вершины З. Р_З =4. Его значение заносим в матрицу кратчайших расстояний, соответствующее звено на рисунке отмечаем стрелкой.

С вершиной З связаны вершины Г, Ж, М, И:

Из всех найденных потенциалов выбираем наименьший, им является потенциал вершины Б. Р_Б =6. Так как найден еще один потенциал вершины Б через вершину А и он оказался больше Р_Б =6, то его вычеркиваем и в дальнейших расчетах не рассматриваем. Значение выбранного потенциала заносим в матрицу кратчайших расстояний, соответствующее звено на рисунке отмечаем стрелкой. С вершиной Б связаны вершины Г и В, однако до вершины В уже найдено наименьшее значение и занесено в таблицу, поэтому определяем потенциал только до вершины Г.

Из всех найденных потенциалов выбираем наименьший, им является потенциал вершины Е. Р_Е =7. Его значение заносим в матрицу кратчайших расстояний, соответствующее звено на рисунке отмечаем стрелкой. С вершиной Е связаны вершины Д, К, Л, М и Ж. До вершины Д уже найдено наименьшее значение и занесено в таблицу, поэтому определяем потенциалы оставшихся вершин.

Из всех найденных потенциалов выбираем наименьший, им является потенциал вершины Г. Р_Г =9. Так как найдены еще потенциалы вершины Г через вершину З и Б, и они оказались больше Р_Г=9, то их в дальнейших расчетах не рассматриваем. Его значение заносим в матрицу кратчайших расстояний, соответствующее звено на рисунке отмечаем стрелкой. С вершиной Г связаны вершины Б, В и З. До вершины Б и В уже найдены наименьшие значения и занесены в таблицу, поэтому определяем потенциал вершины З.

Из всех найденных потенциалов выбираем наименьший, им является потенциал вершины И. Р_И =9. Его значение заносим в матрицу кратчайших расстояний, соответствующее звено на рисунке отмечаем стрелкой. С вершиной И связана вершина Н.

Из всех найденных потенциалов выбираем наименьший, им является потенциал вершины Л. Р_Л =10. Его значение заносим в матрицу кратчайших расстояний, соответствующее звено на рисунке отмечаем стрелкой. С вершиной Л связаны вершины К и М.

Из всех найденных потенциалов выбираем наименьший, им является потенциал вершины Ж. Р_Ж =11. Так как найдены еще потенциалы вершины Ж через вершину В и Е, и они оказались больше Р_Ж=11, то их в дальнейших расчетах не рассматриваем. Значение заносим в матрицу кратчайших расстояний, соответствующее звено на рисунке отмечаем стрелкой. С вершиной Ж связаны вершины Е, В, З и М. До вершины Е, З и В уже найдены наименьшие значения и занесены в таблицу, поэтому определяем потенциал вершины М.

Из всех найденных потенциалов выбираем наименьший, им является потенциал вершины К. Р_К =11. Так как найдены еще потенциалы вершины К через вершину Л и Е, и они оказались больше Р_К=11, то их в дальнейших расчетах не рассматриваем. Значение заносим в матрицу кратчайших расстояний, соответствующее звено на рисунке отмечаем стрелкой. С вершиной К связаны вершины Е, Д и Л. До всех из них наименьшие значения найдены.

Выбираем следующий наименьший потенциал, им является потенциал вершины М. Р_М =18. Так как найдены еще потенциалы вершины М через вершину Л и Е, и они оказались больше Р_М=18, то их в дальнейших расчетах не рассматриваем. С вершиной М связаны вершины Е, Ж, З, Л и Н. До вершины Е,Ж, З и Л уже найдены наименьшие значения и занесены в таблицу, поэтому определяем потенциал вершины Н.

Выбираем последний наименьший потенциал, им является потенциал вершины Н. Р_Н =18.

Таким образом, выбирая на каждом этапе минимальный потенциал, можно с абсолютной уверенностью гарантировать определение кратчайших расстояний и путей проезда от вершины А до всех остальных вершин данной транспортной сети (рис. 6.2).

Далее потенциал следующей вершины, например Б, принимается за 0 и все расчеты повторяются аналогично.

Рис. 7.18. Кратчайшие расстояния от пункта А

Матрица кратчайших расстояний

Источник

6.3 Задача о кратчайшем пути

Одной из наиболее важных оптимизационных задач на сети является задача нахождения цепи, соединяющей два узла – исходный узел S и узел назначения Т, которая имеет минимальную возможную длину. Алгоритм нахождения кратчайшего пути для сетей без циклов предложен Дейкстрой в 1959г. и считается одним из наиболее эффективных. Он основан на приписывании узлам либо временных, либо постоянных пометок и имеет рекурсивный характер. Все вычисления выполняются с использованием информации об уже определенных на предшествующих шагах кратчайших расстояниях.

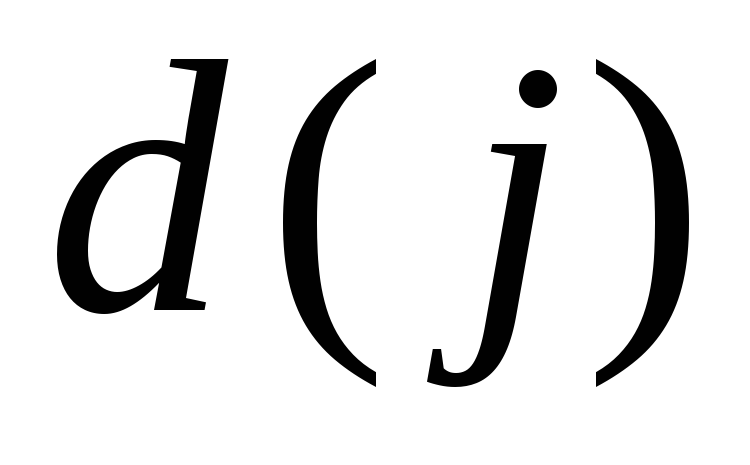
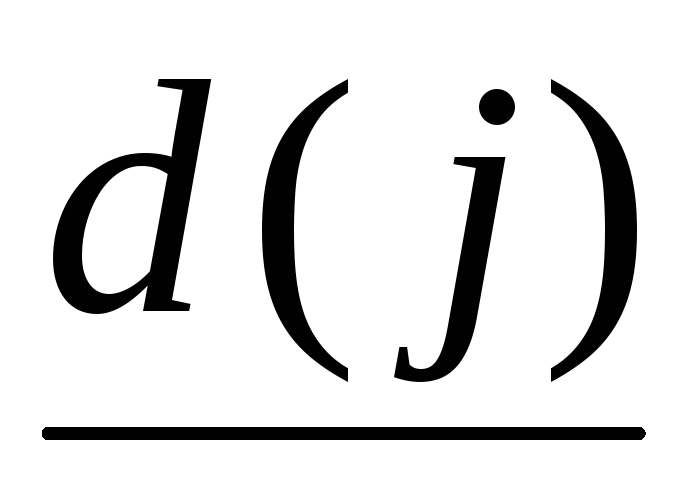
Для заданного узла j через обозначим оценку длины кратчайшей цепи из исходного узла S в этот узел. Если эта оценка не может быть улучшена, то она называется «постоянной пометкой» и обозначается . В противном случае она называется «временной пометкой». Обозначим через y номер вершины, получившей постоянную пометку последней. Алгоритм состоит из трех шагов.

Шаг 1. Всем узлам, кроме исходного, приписываются временные пометки, равные , т.е. . Исходному узлу приписывается постоянная пометка, равная нулю, т.е. и .

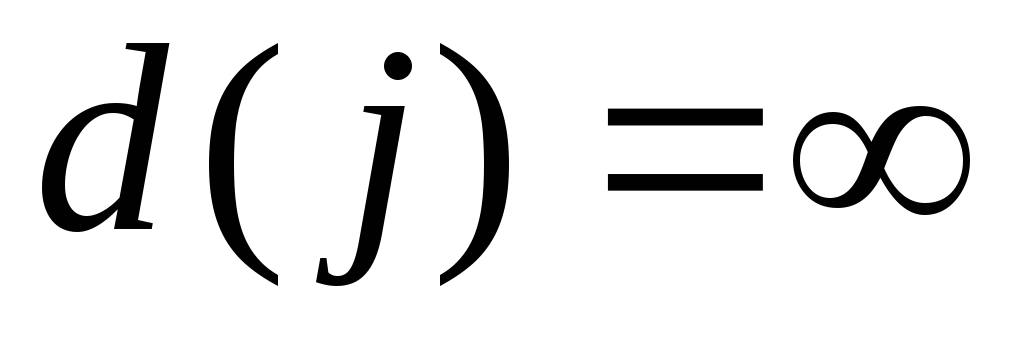
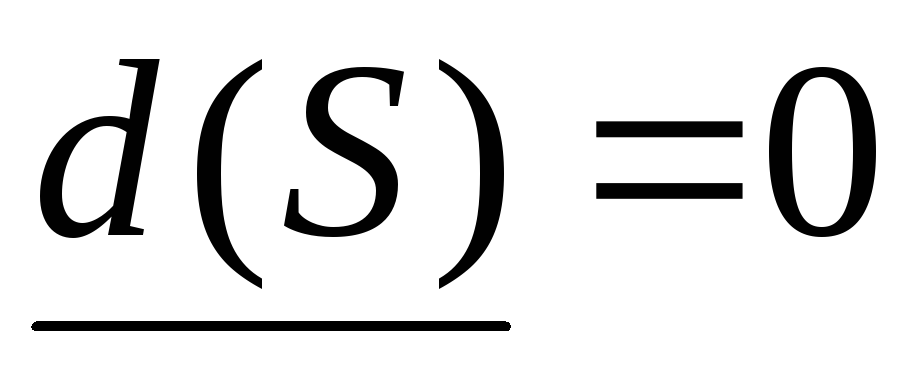
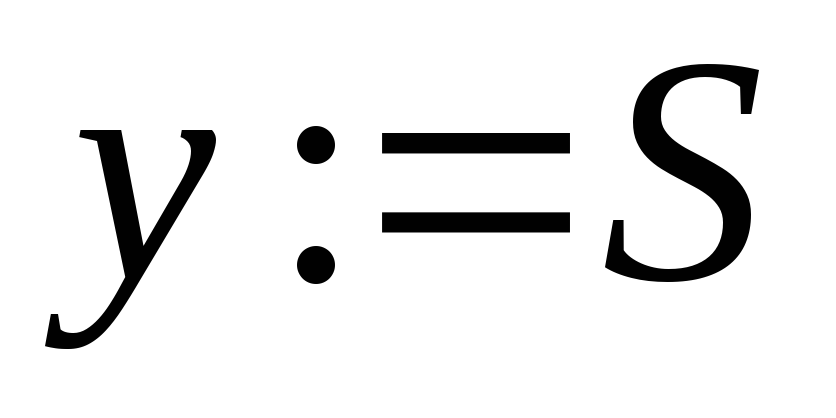
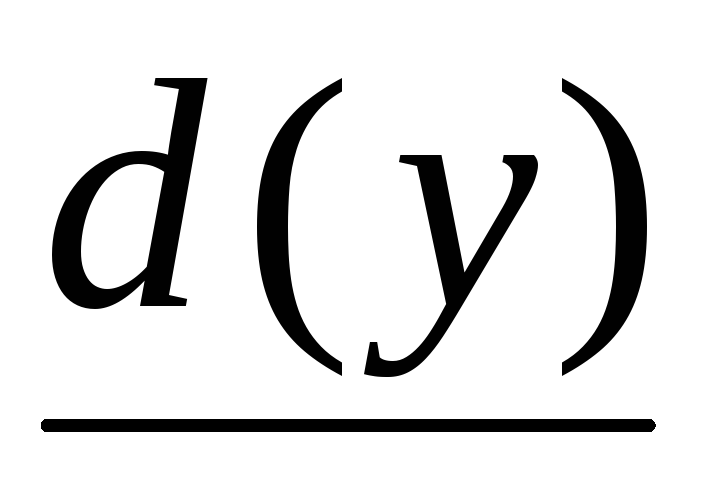
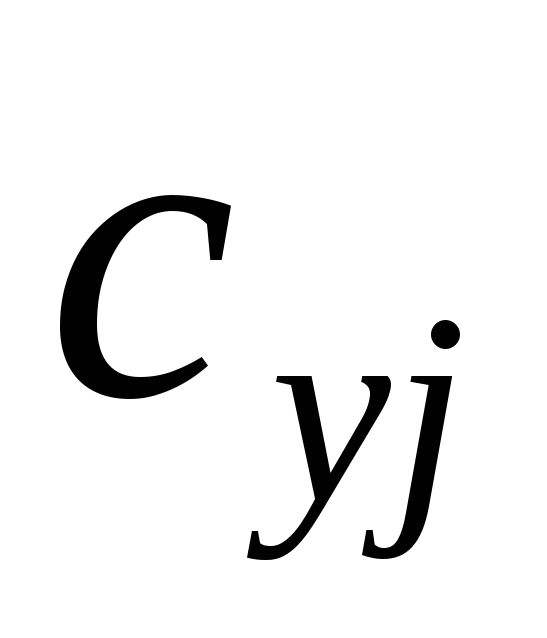
Шаг 2. Рассматриваем все вершины j, смежные с последней получившей постоянную пометку вершиной и имеющие временные пометки. Сравниваем величину временной пометки с суммой величины последней постоянной пометки и длины дуги , ведущей изy в рассматриваемую вершину. Временной пометке рассматриваемого узла присваиваем минимальное значение из двух сравниваемых величин:

.

Среди всех временных пометок выбираем минимальную (пусть это пометка вершины ) и делаем ее постоянной, т.е. и . Кроме того, помечаем дугу , ведущую в выбранную на данном этапе вершину. Если все временные пометки равны бесконечности, т.е. , то в исходном графе отсутствует путь из S в эти вершины и вычисления заканчиваются. Шаг 3. Если последняя постоянная пометка приписана узлу Т , то алгоритм завершает работу: кратчайший путь из вершины S в узел назначения Т найден. Иначе повторяем шаг 2.

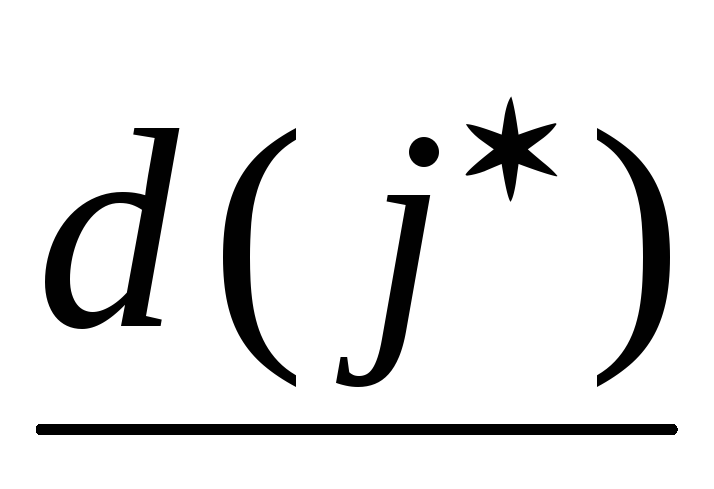
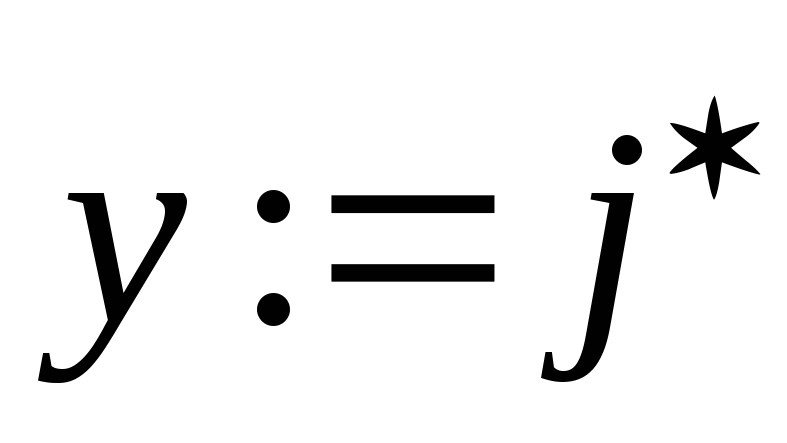
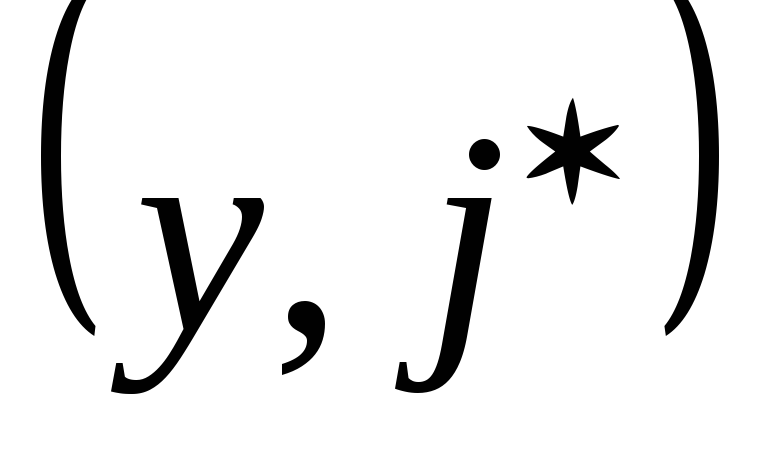
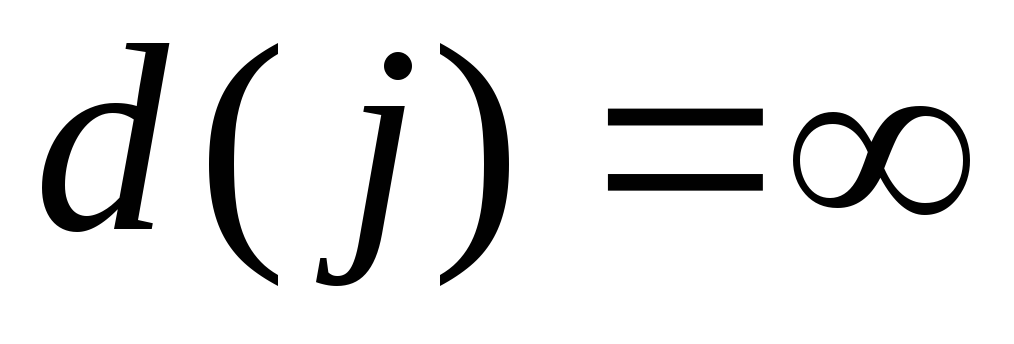
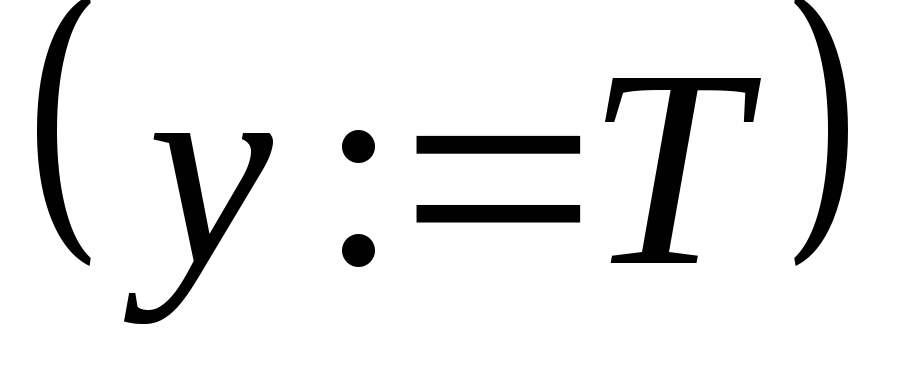
В процессе решения помеченные дуги образуют в исходном графе ориентированное дерево кратчайших путей с корнем в вершине S – т.е. путь от вершины S до любой вершины, принадлежащей дереву, – кратчайший. Кроме этого, если вершина y принадлежит кратчайшему пути из S в j, то часть этого пути, заключенная между у и j, является кратчайшим путем из вершины у в j.

Алгоритм Дейкстры может быть выполнен непосредственно на сети.

Пример. Сеть дорог с двухсторонним движением задана матрицей расстояний в км (матрицей весовых коэффициентов). Необходимо найти для данной сети дорог самый короткий маршрут из пункта 1 в пункт 10.

Источник