Сетевая модель понятие о сетевом планировании

1.2 Основные понятия сетевого планирования

Следует выделить следующие понятия, необходимые для сетевого планирования.

Работа – производственный процесс, требующий затрат времени и материальных ресурсов и приводящий к достижению определенных результатов.

По своей физической природе работы можно рассматривать как действие (например, заливка фундамента бетоном, составление заявки на материалы, изучение конъюнктуры рынка), процесс (пример — старение отливок, выдерживание вина, травление плат) и ожидание (процесс, требующий только затраты времени и не потребляющий никаких ресурсов; является технологическим (твердение цементной стяжки) или организационным (ожидание сухой погоды) перерывом между работами, непосредственно выполняемым друг за другом.

По количеству затрачиваемого времени работа может быть:

• действительной, то есть протяжённым во времени процессом, требующим затрат ресурсов;
• фиктивной (или зависимостью), не требующей затрат времени и представляющей связь между какими-либо работами: передача измененных чертежей от конструкторов к технологам, сдача отчета о технико-экономических показателях работы цеха вышестоящему подразделению.

1.3 Правила построения сетевых моделей

• какие работы должны быть завершены до начала данной работы;
• какие работы должны быть начаты после завершения данной работы;
• какие работы необходимо выполнять одновременно с выполнением данной работы.

Источник

6. Модели сетевого планирования и управления

6.1. Назначение и области применения сетевого планирования и управления

Исходя из функции маркетинга (организации производственного процесса) поиски более эффективных способов планирования сложных процессов привели к созданию принципиально новых методов сетевого планирования и управления (СПУ).

Система методов СПУ – система методов планирования и управления разработкой крупных народнохозяйственных комплексов, научными исследованиями, конструкторской и технологической подготовкой производства, новых видов изделий, строительством и реконструкцией, капитальным ремонтом основных фондов путем применения сетевых графиков.

СПУ основано на моделировании процесса с помощью сетевого графика и представляет собой совокупность расчетных методов, организационных и контрольных мероприятий по планированию и управлению комплексом работ.

• формировать календарный план реализации некоторого комплекса работ;
• выявлять и мобилизовывать резервы времени, трудовые, материальные и денежные ресурсы;

• осуществлять управление комплексом работ по принципу «ведущего звена» с прогнозированием и предупреждением возможных срывов в ходе работ;
• повышать эффективность управления в целом при четком распределении ответственности между руководителями разных уровней и исполнителями работ.

6.2. Сетевая модель и ее основные элементы

Сетевая модель представляет собой план выполнения некоторого комплекса взаимосвязанных работ (операций), заданного в специфической форме сети, графическое изображение которой называется сетевым графиком. Отличительной особенностью сетевой модели является четкое определение всех временных взаимосвязей предстоящих работ. Главными элементами сетевой модели являются события и работы. Работа – протяженный во времени процесс, требующий затрат ресурсов (например, сборка изделия, испытание прибора и т.п.). Каждая действительная работа должна быть конкретной, четко описанной и иметь ответственного исполнителя. Событие — это момент завершения какого-либо процесса, отражающий отдельный этап выполнения проекта. Событие может являться частным результатом отдельной работы или суммарным результатом нескольких работ. Событие может свершиться только тогда, когда закончатся все работы, ему предшествующие. Последующие работы могут начаться только тогда, когда событие свершится. Отсюда двойственный характер события: для всех непосредственно предшествующих ему работ оно является конечным, а для всех непосредственно следующих за ним — начальным. При этом предполагается, что событие не имеет продолжительности и свершается как бы мгновенно. Поэтому каждое событие, включаемое в сетевую модель, должно быть полно, точно и всесторонне определено, его формулировка должна включать в себя результат всех непосредственно предшествующих ему работ. Среди событий сетевой модели выделяют исходное и завершающее события. Исходное событие не имеет предшествующих работ и событий, относящихся к представленному в модели комплексу работ. Завершающее событие не имеет последующих работ и событий. События на сетевом графике (или, как еще говорят, на графе) изображаются кружками (вершинами графа), а работы — стрелками (ориентированными дугами), показывающими связь между работами. Пример фрагмента сетевого графика представлен на рис. 6.1.

Источник

Глава 2. Сетевое планирование 2.1. Основные понятия сетевой модели

Сетевая модель — графическое изображение плана выполнения комплекса работ, состоящего из нитей (работ) и узлов (событий), которые отражают логическую взаимосвязь всех операций. В основе, сетевого моделирования лежит изображение планируемого комплекса работ в виде графа. Сетевой график — это ориентированный граф без контуров. В сетевом моделировании имеются два основных элемента — работа и событие.

Работа — это активный процесс, требующий затрат ресурсов, либо пассивный (ожидание), приводящий к достижению намеченного результата.

Фиктивная работа — это связь между результатами работ (событиями), не требующая затрат времени и ресурсов.

Событие — это результат (промежуточный или конечный) выполнения одной или нескольких предшествующих работ.

Путь — это любая непрерывная последовательность (цепь) работ и событий.

Критический путь — это путь, не имеющий резервов и включающий самые напряженные работы комплекса. Работы, расположенные на критическом пути, называются критическими. Все остальные работы являются некритическими (ненапряженными) и обладают резервами времени, которые позволяют передвигать сроки их выполнения, не влияя на общую продолжительность выполнения всего комплекса работ.

При построении сетевых моделей необходимо соблюдать следующие правила:

1. Сеть вычерчивается слева направо, и каждое событие с большим порядковым номером изображается правее предыдущего. Общее направление стрелок, изображающих работы, также в основном должно быть расположено слева направо, при этом каждая работа должна выходить из события с меньшим номером и входить в событие с большим номером.

2. Два соседних события могут объединяться лишь одной работой. Для изображения параллельных работ вводятся промежуточное событие и фиктивная работа (рис. 9).

3. В сети не должно быть тупиков, т. е. промежуточных событий, из которых не выходит ни одна работа (рис. 10).

4. В сети не должно быть промежуточных событий, которым не предшествует хотя бы одна работа

5. В сети не должно быть замкнутых контуров, состоящих из взаимосвязанных работ, создающих замкнутую цепь (рис. 12).

6. Если одно событие служит началом для двух или более работ, после завершения которых начинается выполнение следующей работы, то вводится штриховая стрелка (условная зависимость) и дополнительное событие со своим номером.

7. Если какие-то работы могут начинаться до полного завершения предыдущей работы, то ее следует разбить на части и считать каждую из них самостоятельной.

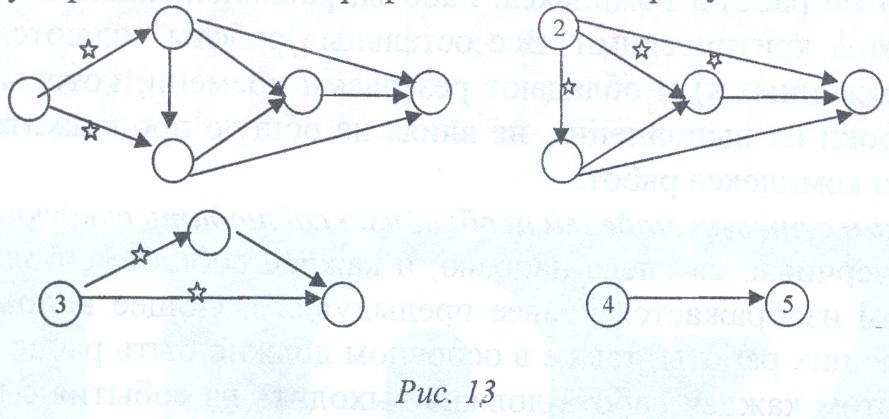
Для правильной нумерации событий поступают следующим образом: нумерация событий начинается с исходного события, которому дается номер 1. из исходного события 1 вычеркивают все исходящие из него работы, на оставшейся сети вновь находят событие, в которое не входит ни одна работа. Этому событию дается номер 2. Затем вычерчивают работы, выходящие из события 2, и вновь находят

на оставшейся части сети событие, в которое не входит ни одна работа, ему присваивается номер 3, и так продолжается до завершающего события. Пример нумерации сетевого графика показан на рисунке 13.

Продолжительность выполнения работ устанавливается на основании действующих нормативов или по экспертным оценкам специалистов. В первом случае временные оценки являются детерминированными (однозначными), во втором — стохастическими (вероятностными).

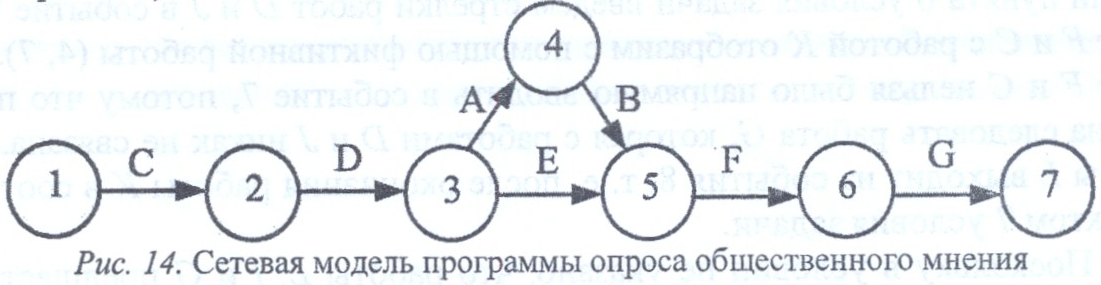
Пример 1. Построить сетевую модель программы опроса общественного мнения, которая включает разработку (А; 1 день) и распечатку анкет

(В; 0,5 дня), прием на работу (С; 2 дня) и обучение (D; 2 дня) персонала, выбор опрашиваемых лиц

(Е; 2 дня), рассылку им анкет (F; 1 день) и анализ полученных данных (G; 5 дней).

Решение. Из условия задачи нам известно содержание работ, но явно не указаны взаимосвязи между работами. Поэтому для их установления необходимо проанализировать смысл каждой конкретной работы и выяснить, какие из остальных работ должны ей непосредственно предшествовать. Исходной работой, начинающей сетевой график, в данном случае является «прием на работу» (С), поскольку все остальные работы должны выполняться уже принятыми на работу сотрудниками (рис. 14). Перед выполнением всех работ по опросу общественного мнения сотрудников необходимо обучить персонал (D). Перед тем как разослать анкеты (F), их надо разработать (А), распечатать (В) и выбрать опрашиваемых лиц (Е), причем работу с анкетами и выбор лиц можно выполнять одновременно. Завершающей работой проекта является анализ полученных данных (G), который нельзя выполнить без предварительной рассылки анкет (F). В результате этих рассуждений построим сетевую модель и пронумеруем события модели (см. рис. 14).

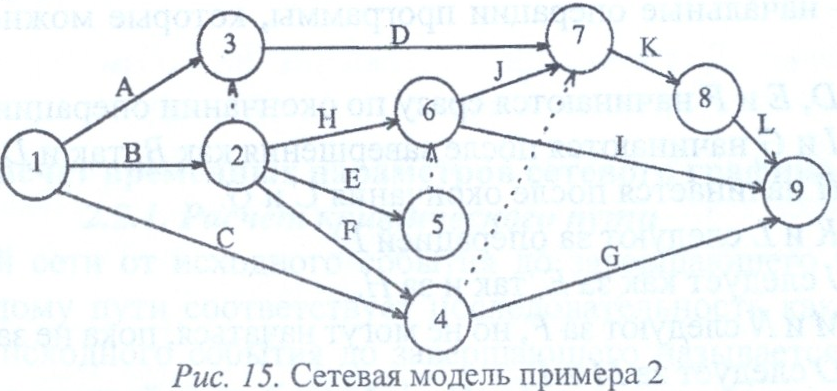
Пример 2. Построить сетевую модель, включающую работы А, В, С, . , L, которая отображает следующее упорядочение работ:

1) А, В и С — исходные операции проекта;

2) А и В предшествуют D;

3) В предшествует Е, F и Н;

4) F и С предшествует G;

5) Е и Н предшествуют I и J;

6) С, D, F и J предшествуют К;

7) К предшествует L.

Решение. В пункте 1 условия явно указано, что А, В и С являются исходными работами, поэтому изобразим их тремя стрелками, выходящими из исходного события 1. Пункт 2 условия означает, что стрелки работ А и В должны окончиться в одном событии, из которого выйдет стрелка работы D. Но поскольку стрелки работ А и В также и начинаются в одном событии, то имеет место параллельность работ, которая недопустима правилами построения сетевых моделей. Для ее устранения введем дополнительное событие 2, в которое войдет работа В, после чего соединим события 2 и 3, в которые входят работы

А и В, пунктирной стрелкой фиктивной работы. В данном случае фиктивная работа (2,3) не соответствует никакой реальной работе, а лишь отображает логическую связь между работами В и D. Дальнейшее построение рассмотрим с помощью рисунка 15.

Согласно пункту 3 условия задачи, из события 2 выходят три стрелки работ Е, F и Н. Согласно пункту 4 условия задачи стрелки работ С и F должны войти в общее событие, из которого выйдет стрелка работы G. Проблема с параллельностью работ Е и Н

(пункт 5 условия задачи) решается путем введения дополнительного события 5 и фиктивной работы

(5, 6). для отображения в сетевой модели пункта 6 условия задачи введем стрелки работ D и J в событие 7, а связь работ F и С с работой К отобразим с помощью фиктивной работы (4,7). Стрелки работ F и С нельзя было напрямую вводить в событие 7,

потому что после них должна следовать работа G, которая с работами D и J никак не связана. Стрелка работы L выходит из события 8, т. е. после окончания работы К в соответствии с пунктом 7 условия задачи.

Поскольку в условии не указано, что работы L, I и G предшествуют каким-либо другим работам, то эти работы являются завершающими и их стрелки войдут в завершающее событие 9. Нумерацию событий проводят после построения сетевого графика, следя за тем, чтобы номер начального события каждой работы был меньше номера ее конечного события.

Источник