Сетевая модель представленная в графическом виде

1. Сетевая модель и ее основные элементы.

Сетевая модель представляет собой план выполнения некоторого комплекса взаимосвязанных работ (операций), заданного в специфической форме сети, графическое изображение которой называется сетевым графиком. Отличительной особенностью сетевой модели является четкое определение всех временных взаимосвязей предстоящих работ.

Главными элементами сетевой модели являются событиями и работы

Термин работа используется в СПУ в широком смысле.Во-первых, это действительная работа — протяженный во временипроцесс, требующий затрат ресурсов (например, сборка изделия, испытание прибора и т.п.). Каждая действительная работа, должна быть конкретной, четко описанной и иметь ответст­венного исполнителя.

Во-вторых, это ожидание — протяженный во времени процесс,не требующий затрат труда (например, процесс сушки после окраски, старения металла, твердения бетона и т.п.).

В-третьих, это зависимость, или фиктивная работа — логическая связь между двумя или несколькими работами (события), не требующими затрат труда, материальных ресурсов или времени. Она указывает, что возможность одной работы непосредственно зависит от результатов другой. Естественно, что продолжительность фиктивной работы принимается равной нулю.

Событие — это момент завершения какого-либо процесса, отражающий отдельный этап выполнения проекта. Событие может являться частным результатом отдельной работы или суммарным результатом нескольких работ. Событие может свершиться только тогда, когда закончатся все работы, ему предшествующие. Последующие работы могут начаться только тогда, когда событие свершится. Отсюда двойственный характер события: для всех непо­средственно предшествующих ему работ оно является конечным, а для всех непосредст­венно следующих за ним — начальным. При этом предполагается, что событие не имеет продолжительности и свершается как бы мгновенно. Поэтому каждое событие, включаемое в сетевую модель, должно быть полно, точно и всесторонне определено, его формулировка должна включать в себя результат всех непосредственно предшествующих ему работ.

Среди событий сетевой модели выделяют исходное и завершающее события. Исходное собы­тие не имеет предшествующих работ и событий, относящихся к представленному в модели комплексу работ. Завершающее событие не имеет последующих работ и событий.

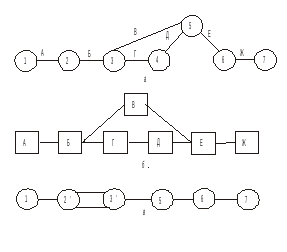
События на сетевом графике (или, как еще говорят, на графе)изображаются кружками (вершинами графа), а работы — стрелками(ориентированными дугами), показывающими связь между работами. Пример фрагмента сетевого графика представлен на рис 1:

На рис. 2, а приведен сетевой график задачи моделирования и построения оптималь­ного плана некоторого экономического объекта. Чтобы решить эту задачу, необходимо провести следующие работы: А – сформулировать проблему исследования; В5 — матема­тическую модель изучаемого объекта; В — собрать информацию; Г — выбрать метод решения задачи; Д — построить и отладить программу для ЭВМ; Е — рассчитать опти­мальный план; Ж — передать результаты расчета заказчику. Цифрами на графике обозначены номера событий, к которым приводит выполнение соответствующих работ.

Из графика, например, следует, что работы В и Г можно начать выполнять независимо одна от другой только после свершения события 3, т.е. когда выполнены работы А и Б; работу Д — после свершения события 4, когда выполнены работы А, Б и Г; а работу Е можно выполнить только после наступления события 5, т.е. при выполнении всех предшествующих ему работ А, Б, В, Г и Д.

В сетевой модели, представленной на рис. 2 а, нет числовых оценок. Такая сеть называется структурной. Однако на практике чаще всего используются сети, в которых заданы оценки про­должительности работ (указываемые в часах, неделях, декадах, месяцах и т.д. над соответствую­щими стрелками), а также оценки других параметров, например трудоемкости, стоимости и т.п. Именно такие сети мы будем рассматривать в дальнейшем.

Но прежде сделаем следующее замечание. В рассмотренных примерах сетевые графики со­стояли из работ и событий. Однако может быть и иной принцип построения сетей — без событий. В такой сети вершины графа (например, изображенные прямоугольниками) означают определен­ные работы, а стрелки — зависимости между этими работами, определяющие порядок их выполнения. В качестве примера сетевой график «события — работы» задачи моделирования и построе­ния оптимального плана некоторого экономического объекта, приведенный на рис. 2 а, пред­ставлен в виде сети «работы — связи» на рис. 2 б. А сетевой график «события — работы» той же задачи, но с неудачно составленным перечнем работ, представлен на рис. 2 в (см. правило 3 в разд. 3).

Следует отметить, что сетевой график «работы — связи» в отличие от графика «события — ра­боты» обладает известными преимуществами: не содержит фиктивных работ, имеет более про­стую технику построения и перестройки, включает только хорошо знакомое исполнителям понятие работы без менее привычного понятия события. Вместе с тем сети без событий оказываются значительно более громоздкими, так как событий обычно значительно меньше, чем работ (пока­затель сложности сети, равный отношению числа работ к числу событий, как правило, существенно больше единицы). Поэтому эти сети менее эффективны с точки зрения управления ком­плексом. Этим и объясняется тот факт, что (при отсутствии в целом принципиальных различий между двумя формами пред­ставления сети) в настоящее время наибольшее распространение получили сетевые графики «со­бытия — работы».

Источник

2.5. Сетевые модели и сетевые графики

Сетевая диаграмма (сеть, граф сети, PERT-диаграмма) – графическое отображение работ проекта и зависимостей между ними. В планировании и управлении проектами под термином «сеть» понимается полный комплекс работ и вех проекта с установленными между ними зависимостями.

Сетевые диаграммы отображают сетевую модель в графическом виде как множество вершин, соответствующих работам, связанных линиями, представляющими взаимосвязи между работами. Этот граф, называемый сетью типа «вершина–работа» или диаграммой предшествования–следования, является наиболее распространенным представлением сети.

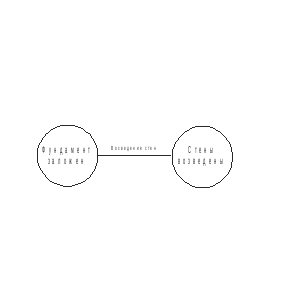
Существует другой тип сетевой диаграммы – сеть типа «вершина–событие», который на практике используется реже. При данном подходе работа представляется в виде линии между двумя событиями (узлами графа), которые, в свою очередь, отображают начало и конец данной работы. PERT-диаграммы являются примерами этого типа диаграмм (рис. 2.1).

Рис. 2.1. Фрагмент сети «вершина–событие»

Сетевая диаграмма не является блок-схемой в том смысле, в котором это средство используется для моделирования деловых процессов. Принципиальным отличием от блок-схемы является то, что сетевая диаграмма отображает только логические зависимости между работами, а не входы, процессы и выходы, а также не допускает повторяющихся циклов или так называемых петель (в терминологии графов – ребро графа, исходящее из вершины и возвращающееся в ту же вершину, рис. 2.2).

Рис. 22. Пример петли в сетевой модели

Методы сетевого планирования – методы, основная цель которых заключается в том, чтобы сократить до минимума продолжительность проекта. Основываются на разработанных практически одновременно и независимо методе критического пути МКП (СРМ – Critical Path Method) и методе оценки и пересмотра планов ПЕРТ (PERT – Program Evaluation and Review Technique).

Критический путь – максимальный по продолжительности полный путь в сети называется критическим; работы, лежащие на этом пути, также называются критическими. Именно длительность критического пути определяет наименьшую общую продолжительность работ по проекту в целом.

Длительность выполнения всего проекта в целом может быть сокращена за счет сокращения длительности работ, лежащих на критическом пути. Соответственно любая задержка выполнения работ критического пути повлечет увеличение длительности проекта.

Метод критического пути позволяет рассчитать возможные календарные графики выполнения комплекса работ на основе описанной логической структуры сети и оценок продолжительности выполнения каждой работы, определить критический путь для проекта в целом.

Полный резерв времени, или запас времени, – это разность между датами позднего и раннего окончаний (начал) работы. Управленческий смысл резерва времени заключается в том, что при необходимости урегулировать технологические, ресурсные или финансовые ограничения проекта он позволяет руководителю проекта задержать работу на этот срок без влияния на срок завершения проекта в целом. Работы, лежащие на критическом пути, имеют временной резерв, равный нулю.

Диаграмма Ганнта – горизонтальная линейная диаграмма, на которой задачи проекта представляются протяженными во времени отрезками, характеризующимися датами начала и окончания, задержками и, возможно, другими временными параметрами.

Процесс сетевого планирования предполагает, что вся деятельность будет описана в виде комплекса работ или работ с определенными взаимосвязями между ними. Для расчета и анализа сетевого графика используется набор сетевых процедур, известных под названием «процедуры метода критического пути».

Процесс разработки сетевой модели включает в себя: определение списка работ проекта; оценку параметров работ; определение зависимостей между работами. Определение комплекса работ проводится для описания деятельности по проекту в целом, с учетом всех возможных работ. Работа является основным элементом сетевой модели. Под работами понимается деятельность, которую необходимо выполнить для получения конкретных результатов. Пакеты работ определяют деятельность, которую необходимо осуществить для достижения результатов проекта, которые могут выделяться вехами. Прежде чем начать разработку сетевой модели, необходимо убедиться, что на нижнем уровне СРР определены все работы, обеспечивающие достижение всех частных целей проекта. Сетевая модель образуется в результате определения зависимостей между этими работами и добавления связующих работ и событий. В общем виде данный подход основан на предположении, что каждая работа направлена на достижение частного результата. Связующие работы, возможно, и не требуют получения какого-либо материального конечного результата, например работа «организация исполнения».

Оценка параметров работ является ключевой задачей руководителя проекта, привлекающего для решения этой задачи членов команды, ответственных за реализацию отдельных частей проекта.

Ценность календарных графиков, стоимостных и ресурсных планов, получаемых в результате анализа сетевой модели, полностью зависит от точности оценок продолжительности работ, а также оценок потребностей работ в ресурсах и финансовых средствах.

Оценки должны производиться для каждой детальной работы, а затем могут быть агрегированы и обобщаться по каждому из уровней СРР в плане проекта. Продолжительность (длительность) работы определяет время, которое предполагается затратить на ее выполнение. Оценки длительности каждой детальной работы выполняются на основе предыдущего опыта и количества планируемых на работу исполнителей. Облегчает эту процедуру то, что оценки необходимо делать для детальных работ проекта, которые представляют собой, как правило, элементарные виды деятельности.

Основными являются два типа работ:

• работа с фиксированной продолжительностью имеет определенную длительность, которая не зависит от количества назначенных ей ресурсов: нельзя ускорить выполнение работы, назначив, например, вдвое больше исполнителей, поскольку существуют факторы, влияющие на длительность работы, но не зависящие от количества исполнителей;
• работа с фиксированным объемом имеет длительность, зависящую от количества назначенных исполнителей (ресурсов). Таким образом, для работ, продолжительность которых зависит от количества доступных ресурсов, возможен вариант непосредственного расчета длительности исходя из информации о требуемых объемах работ (например, в человеко-днях) и количестве доступных ресурсов. В этом случае увеличение числа исполнителей приведет к сокращению времени выполнения работы.

• «начало после окончания». Это стандартная последовательность, при которой предшествующая работа должна завершиться до начала последующей;
• «начало после начала». Это наиболее общая последовательность при моделировании работ, которые должны выполняться одновременно. В этом случае не требуется завершения предшествующей работы до начала последующей. Для ее начала необходимо, чтобы предшествующая работа только началась;
• «окончание после окончания». Этот тип зависимости также используется для моделирования параллельных работ. В этом случае окончание последующей работы контролируется окончанием работы предшественницы;
• «окончание после начала». Этот тип зависимости используется довольно редко и применяется прежде всего для работ, выполняемых вахтовым методом.

Источник