Анализ сетевого графика
Созданный сетевой график можно сохранить в форматах docx и png (меню Действия ). Далее можно найти параметры сетевой модели (критический путь, резервы времени, построить диаграмму Ганта и многое другое).
Инструкция к сервису
Для добавления вершины на графическое полотно необходимо использовать соответствующую фигуре кнопку Добавить . Новый объект также можно вставить, предварительно выделив его левой кнопкой мыши, а затем щелкнуть мышкой на рабочем поле. Нумерация вершин может начинаться с 0 , для этого нужно снять отметку с пункта Нумерация вершин с №1 .
Чтобы соединить вершины, их необходимо предварительно выбрать (один клик мыши по объекту), а затем нажать на кнопку Соединить .
Сетевая модель может быть представлена в табличной форме и в виде матрицы весов (матрицы расстояний). Чтобы использовать данные представления, выберите меню Операции .
Построенный граф можно сохранить в формате docx или png .
Если в качестве формы вершин используется прямоугольник, то при построении секторальной диаграммы применяется методология Microsoft Visio с отображением параметров duration, ES, EF, LS, LF, and slack.
Основные определения
- «действительная работа» – процесс, требующий затрат времени и ресурсов;
- «фиктивная работа» – логическая связь между двумя или несколькими работами, указывающая на то, что начало одной работы зависит от результатов другой. Фиктивная работа не требует затрат времени и ресурсов, продолжительность ее равна нулю.
Правила построения сетевой модели
- в сети не должно быть «тупиков», т.е., событий, от которых не начинается ни одна работа, исключая завершающее событие графика;
- В сетевом графике не должно быть «хвостовых» событий, то есть событий, которым не предшествует хотя бы одна работа, за исключением исходного.
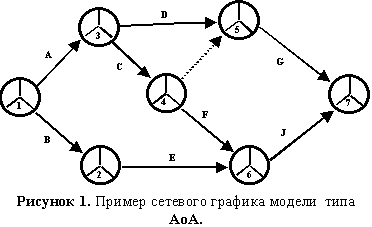
- в сети не должно быть замкнутых контуров (рис.1);
- Любые два события должны быть непосредственно связаны не более чем одной работой.
- В сети рекомендуется иметь одно исходное и одно завершающее событие.
- Сетевой график должен быть упорядочен. То есть события и работы должны располагаться так, чтобы для любой работы предшествующее ей событие было расположено левее и имело меньший номер по сравнению с завершающим эту работу событием.
Методы оптимизации сетевого графика
Логико-математическое описание, формирование планов и управляющих воздействий осуществляется на базе использования особого класса моделей, называемых сетевыми моделями.
После построения и расчета сетевого графика (определения его параметров), выполнения анализа графика, заключающегося в оценке его целесообразности и структуры, оценке загрузки исполнителей, оценке вероятности наступления завершающего события в заданный срок, следует приступать к оптимизации сетевого графика. Процедура оптимизации заключается в приведение графика в соответствие с заданными сроками выполнения работ, возможностями подрядных организаций и т.д. В общем случае под оптимизацией следует понимать процесс улучшения организации выполнения работ.
- Оптимизация сетевой модели по критерию «число исполнителей». Заполняется столбец Количество исполнителей Ч ►
- Оптимизация сетевой модели по критерию «время – стоимость» ( время — затраты ). В случае известных коэффициентов затрат на ускорение работ заполняется только этот столбец h(i,j) . Иначе, заполняются столбцы tопт (Нормальный режим), Минимальное время работ, tmin (Ускоренный режим), Нормальная стоимость, Cн и Срочная стоимость, Cc .
Теоретические основы проектного управления
Для описания, анализа и оптимизации проектов наиболее подходящими оказались сетевые модели.
В сетевой модели роль вершин графа могут играть события, определяющие начало и окончание отдельных работ, а дуги в этом случае будут соответствовать работам. Такую сетевую модель принято называть сетевой моделью с работами на дугах (Activities on Arrows, AoA). В то же время, возможно, что в сетевой модели роль вершин графа играют работы, а дуги отображают соответствие между окончанием одной работы и началом другой. Такую сетевую модель принято называть сетевой моделью с работами в узлах (Activities on Nodes, AoN).
Пусть множество A= – комплекс работ, выполнение которых требуется для решения определенной задачи, например, строительства дома. Тогда, если множество V= будет представлять комплекс событий, возникающих в процессе выполнения комплекса работ, то сетевая модель будет задаваться ориентированным графом G=(V, A), в котором элементы множества V играют роль вершин, а элементы множества A – роль дуг, соединяющих вершины, причем каждой дуге ai можно поставить в однозначное соответствие пару вершин (vsi, vfi), первая из которых будет определять момент начала работы аi, а вторая – момент окончания этой работы. Такая сетевая модель будет сетевой моделью с работами на дугах.
Теперь пусть множество A= – по-прежнему будет рассматриваться как комплекс работ, выполнение которых требуется для решения определенной задачи, например, строительства дома. Тогда, если множество V= будет представлять комплекс отношений предшествования-следования работ в процессе их выполнения, то сетевая модель будет задаваться ориентированным графом G=(A, V), в котором элементы множества A играют роль вершин, а элементы множества V – роль дуг, соединяющих вершины, причем каждой дуге vi можно поставить в однозначное соответствие пару вершин (asi, afi), первая из которых будет непосредственно предшествующей работой в данной паре, а вторая – непосредственно следующей. Такая сетевая модель будет сетевой моделью с работами в узлах.
Сетевая модель может быть представлена: 1) сетевым графиком, 2) в табличной форме, 3) в матричной форме, 4) в форме диаграммы на шкале времени. Как будет показано ниже, переход от одной формы представления к другой не составляет большого труда.
Преимущество сетевых графиков и временных диаграмм перед табличной и матричной формами представления состоит в их наглядности. Однако это преимущество исчезает прямо пропорционально тому, как увеличиваются размеры сетевой модели. Для реальных задач сетевого моделирования, в которых речь идет о тысячах работ и событий, вычерчивание сетевых графиков и диаграмм теряет всякий смысл.
Преимущество табличной и матричной формы перед графическими представлениями состоит в том, что с их помощью удобно осуществлять анализ параметров сетевых моделей; в этих формах применимы алгоритмические процедуры анализа, выполнение которых не требует наглядного отображения модели на плоскости.
Сетевым графиком называется полное графическое отображение структуры сетевой модели на плоскости.
Если сетевым графиком на плоскости отображается сетевая модель типа АоА, то однозначное представление должны получить все работы и все события модели. Однако структура сетевого графика модели АоА может быть более избыточна, чем структура самой отображаемой сетевой модели. Дело в том, что по правилам построения сетевого графика для удобства его анализа необходимо, чтобы два события были соединены только единственной работой, что в принципе не соответствует реальным обстоятельствам в окружающей нас действительности. Поэтому принято вводить в структуру сетевого графика элемент, которого нет ни в действительности, ни в сетевой модели. Этот элемент называется фиктивной работой. Таким образом, структура сетевого графика образуется из трех типов элементов (в отличие от структуры сетевой модели, где только два типа элементов):
- событий – моментов времени, когда происходит начало или окончание выполнения какой-либо работы (работ);
- работ – неделимых частей комплекса действий, необходимых для решения некоторой задачи;
- фиктивных работ – условных элементов структуры сетевого графика, используемых исключительно для указания логической связи отдельных событий.
Графически события изображаются кружками, разделенными на три равных сегмента (радиусами под углом в 120°); работы изображаются сплошными линиями со стрелками на конце, ориентированными слева направо; фиктивные работы изображаются пунктирными линиями со стрелками на конце, ориентированными слева направо. Пример сетевого графика модели АоА представлен ниже на рис. 1.
Отметим, что индексация работ производится рядом с соответствующими стрелками; фиктивные работы не индексируются; индексы событий проставляются в нижнем сегменте соответствующего кружка. Заполнение остальных сегментов рассматривается ниже.
Если сетевым графиком отображается модель типа AoN, то избыточности структуры удается избежать. Здесь нет необходимости вводить в качестве дополнительного структурного элемента фиктивные работы, поскольку отсутствуют те структурные элементы, которые они призваны обслуживать, а именно – события. В сетевом графике модели типа AoN есть только узлы (или вершины), которые обозначают работы и дуги (сплошные линии со стрелками, ориентированными слева направо), которые обозначают отношения предшествования-следования работ. Никаких событий и никаких фиктивных работ! Заметим, что в наиболее известной программе по проектному управлению Microsoft Project реализуется именно этот тип модели.
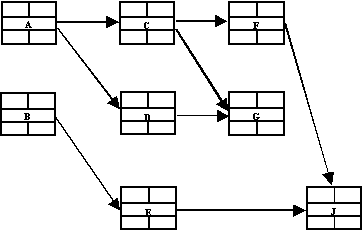
Здесь узлы сети, соответствующие работам, принято изображать прямоугольниками, поделенными на 5 секторов. В центральном секторе проставляется индекс (или записывается наименование работы). Заполнение остальных секторов рассматривается ниже. Пример сетевого графика для модели типа AoN представлен ниже на рис. 2.
Рисунок 2. Пример сетевого графика модели типа АоN.
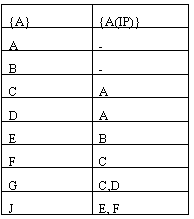
В табличной форме сетевая модель задается множеством , где А – это множество индексов работ, а A(IP) множество комбинаций работ, непосредственно предшествующих работе А. Для рассматриваемого выше примера табличная форма сетевой модели будет такой, которая представлена в табл. 1.
Таблица 1. Табличная форма сетевой модели.
Матричная форма описания сетевой модели задается в виде отношения между событиями (ei, ej), которое равно 1, если между этими событиями есть работа (либо реальная, либо фиктивная) и 0 – в противном случае. Матричная форма для описания сетевой модели из рассматриваемого выше примера приведена ниже в табл. 2: