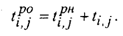Сетевая модель раннее начало

27.Аналитические параметры сетевых графиков

Сетевые модели представляют собой графо-аналитические организацион­ные инструменты.

Прежде всего определяются раннее начало и раннее окончание каждой работы. Затем — позднее начало и позднее окончание каждой работы. Далее критические работы (работы, лежащие на крити­ческом пути и не имеющие резервов времени) и резервы времени для некритических работ. И наконец, определяется так называемый коэф­фициент напряженности каждой работы.

28. Определение ранних начал и ранних окончаний работ сетевой модели

Ранние начала и ранние окончания работ сетевой модели определяют последовательно, слева направо по графику, т.е. от исходного события сети к завершающему. Для всех работ, выходящих из исходного события сети, раннее начало всегда равно нулю.

Прежде чем определить величину раннего начала для всех последующих работ, необходимо определить раннее окончание работ, выходящих из исходного события сети. Раннее окончание для всех работ сетевого графика будет равно сумме раннего начала работы и ее продолжительно­сти. Очевидно, что все работы, которые выходят из одного и того же события, всегда имеют одно и то же раннее начало. Определив раннее начало для одной работы, мы можем записать то же значение раннего начала абсолютно для всех работ, выходящих из того же события, что и данная работа.

29. Определение поздних начал и поздних окончаний работ сетевой модели

Поздние начала и поздние окончания работ в отличие от ранних начал и окончаний определяются в обратном порядке — от завершающего события графика к исходному, т.е. справа налево по графику.

Чтобы определить поздние начала этих работ, необходимо принять во внимание, что начинать эти работы нужно в такой момент, чтобы успеть выполнить данные работы в заданные для них промежутки времени, т.е. закончить каждую работу в самый поздний срок, допустимый для ее окончания.Таким образом, позднее начало данной работы равно позднему окончанию этой работы минус ее продолжительность.

30. Определение работ, составляющих критический путь

Работа характеризует любое действие, требующее затрат времени или ресурсов. Работами считаются и процессы, не требующие затрат времени и ресурсов, а устанавливающие зависимости выполнения работ. Такие работы называются фиктивными. Работа обозначается парой чисел (i,j) где i – номер события, являющимся начальным для данной работы, j – номер события, являющимся конечным для данной работы, в которое она входит. Работа не может начаться раньше, чем свершится событие, являющееся для нее начальным. Каждая работа имеет свою продолжительность t(i,j). Работы на графах обозначаются дугами (стрелками), фиктивные работы обозначаются пунктирными стрелками.

Событиями называются начало или завершение одной или нескольких работ. Они не имеют протяженности во времени. Событие совершается в тот момент, когда оканчивается последняя работа, входящая в него. На графе события изображаются кружками, внутри которых записывается номер события. В моделях СП имеется одно начальное событие (номер 0), одно конечное событие или завершающее (номер N) и промежуточные события (номер i). В графической интерпретации сетевой модели работы представляются дугами, а события – вершинами графа.

Путь – цепочка следующих друг за другом работ (дуг), соединяющих начальную и конечную его вершины. Полный путь L – путь, начало которого совпадает с начальным событием сети, а конец – с завершающим. Продолжительность пути определяется суммой продолжительностей составляющих его работ. Путь, имеющий максимальную продолжительность, называют критическим (обозначение Lкр). Продолжительность критического пути обозначается как tкр_.

Работы, принадлежащие критическому пути, называются критическими. Их несвоевременное выполнение ведет к срыву сроков всего комплекса работ.

Источник

Параметры сетевых моделей и методы их расчета

Сетевая модель имеет ряд характеристик, которые позволяют определить степень напряженности выполнения отдельных работ, а также всего их комплекса и принять решение о перераспределении ресурсов.
Ранний срок наступления события t_р(i) — самый ранний из возможных сроков наступления события. Он равен продолжительности максимального пути от исходного события до данного.
t_р(i) = max t[L_р(i)] (2.1)
Например, t_р(7)=19, т.к. L₁=(1,2,4,7), L₂=(1,3,4,7),
t(L₁)=5+12=17 < t(L₂)=7+12=19.
Ранний срок начала работы t_р.н.(i,j) равен продолжительности максимального пути от исходного до начального события данной работы.
t_р.н.(i,j)=max t[L_n(i)](2.2)
Например, t_р.н.(7,11)=19, т.к. L₁=(1,2,4,7), L₂=(1,3,4,7),
t(L₁)=5+12=17 2)=7+12=19.
Ранний срок начала работы равен раннему сроку наступления начального события данной работы.
t_р.н.(i,j) = t_р(i) (2.3)
Ранний срок окончания работы t_р.о.( i,j) равен сумме раннего срока начала работы и продолжительности данной работы.
t_р.о.(i,j)= t_р.н.(i,j) + t(i,j) (2.4)
Например, t_р.о.(7,11)= t_р.н.(7,11) + t(7,11)= 19+8=27.
Поздний срок наступления события t_п( i) равен разности между продолжительностью критического пути и продолжительностью максимального пути от данного события до завершающего.
t_п(i) =T_кр — max t[L_к(i)](2.5)
Например, t_п(7)=19, т.к. L₁=(7,11), L₂=(7,9,11), t(L₁)=8 > t(L₂)=4,
t_п(7) = T_кр — max t[L_к(7)]=27 — 8=19.
Для событий критического пути t_р( i)=t_п(i), для других событий t_р(i)t_п(i).
Поздний срок окончания работы t_п.о.( i,j) – это самый поздний срок окончания работы, при котором планируемый срок окончания проекта не меняется, он равен разности между продолжительностью критического пути и продолжительностью максимального пути от конечного события данной работы до завершающего события.
t_п.о.(i,j)=T_кр — max t[L_к(j)] (2.6)
Поздний срок окончания работы равен позднему сроку наступления конечного события t_п.о.(i,j) = t_п(j). Например, t_п.о.(4,7) = t_п(7)=19.
Поздний срок начала работы t_п.н.( i,j) – самый поздний срок начала работы, при котором планируемый срок окончания проекта не меняется.
t_п.н.(i,j)= t_{п .о.}(i,j) — t(i,j) (2.7)
Например, t_п.н.(4,7)= t_п.о.(4,7) — t(4,7)=19-12=7.
Для работ критического пути ранние и поздние сроки начала и окончания работ равны: t_р.н.(4,7)= t_п.н.(4,7)=7, t_р.о.(4,7)= t_п.о.(4,7)=19.
Работы, не лежащие на критическом пути, могут иметь резервы времени.
Полный резерв времени R_п( i,j) – максимальное время, на которое можно увеличить продолжительность данной работы, не изменяя продолжительности критического пути.
R_п (i,j)= t_п(j) — t_р(i) — t(i,j)
R_п(i,j)= t_п.н (i,j) — t_р.н.(i,j) (2.8)
R_п (i,j)= t_п.о.(i,j) — t_р.о.(i,j)
Свободный резерв времени R_с( i,j) равен разности между ранним началом последующей работы и ранним окончанием рассматриваемой работы.
R_с(i,j)= t_р.н (j,к) — t_р.о.(i,j) (2.9) Перейти к онлайн решению своей задачи

Читайте также:  Компьютерные сети топология сетей объединение компьютеров в локальную сеть

Источник

7.8. Расчет сетевых моделей непосредственно на графике

Метод расчёта сетевых моделей непосредственно на её графиче­ском представлении используется в том случае, когда количество со­бытий в сетевой модели небольшое.

Пусть имеется та же сетевая модель, которую мы рассчитали табличным методом:

Для расчета сетевой модели непосредственно на графике, каж­дое событие делят на четыре сектора (А, Б, В, Г), в которых указывают следующие данные:

Б — раннее начало работ, выходящих из рассматриваемого события;

В — позднее окончание работ, входящих в рассматривае­мое событие;

Г- номер события, из которого к данному идет максимальный путь.

Алгоритм расчета

1. Расчет ранних начал работ осуществляется на графической модели слева направо. Данные расчета записываются в секторе Б.

1.1. Раннее начало работ, выходящих из исходного события, равно нулю. Номер события, из которого к данному идет максималь­ный путь, также равен нулю, т. к. предшествующего события нет.

1.2. Для каждого следующего события в его секторе Б записы­вают раннее начало работ, выходящих из него. Если в рассматривае­мое событие входит одна работа, то это значение равно раннему на­чалу входящей работы плюс ее продолжительность:

Если же в рассматриваемое событие входят несколько работ, то раннее начало выходящих из него работ равно максимальному из окончаний всех входящих в него работ:

Например, для события 2 в его секторе Б записывают 2, т. к. max (0 + 2) = 2. Для события 3 записывают 5, т. к.: мах(2 + 3; 0 +4) = 5.

2. Одновременно в секторе Г рассматриваемого события запи­сывают номер события, из которого к данному событию идет макси­мальный путь. Например, для события 2 максимальный путь идет из события 1, а для события 3 — из события 2.

Читайте также:  Угрозы в компьютерных сетях это

3. Расчет поздних окончаний работ выполняют, начиная из за­вершающего события до начального.

3.1. Для завершающего события j (в нашем случае j = 7) позднее окончание входящих в него работ равно максимальному значению из ранних окончаний всех входящих в событие j работ:

Здесь maxj читается так: максимальное значение из входящих в событие j работ. В нашем случае, позднее окончание работ, входящих з событие7 = 7, равно:

для работы 6 — 7 : 14 + 1 = 15;

3.2. Позднее окончание работ, выходящих из других событий, оп­ределяется следующим образом:

а) если из рассматриваемого события выходит одна работа, то позднее окончание всех входящих в это событие работ равно поздне­му окончанию выходящей из него работы минус ее продолжитель­ность:

Например, для события № 6 позднее окончание работ 2-6 и 5-6 эавно 17-1 = 16;

б) если же из рассматриваемого события выходит несколько ра­бот, то позднее окончание всех входящих в данное событие работ эавно минимальному из значений разности позднего окончания выхо­дящих работ и их продолжительности:

Например, для события № 4 позднее окончание работы 1- 4 -авно min(13 — 2; 17 — 9) = 8.

4. Критический путь по направлению к исходному событию называет номер события, из которого к рассматриваемому событию см. значение сектора Г рассматриваемого события) идет максималь­ный путь. Если рассматривать путь от завершающего события, то он роходит через те события /, в которых раннее начало выходящих из его работ и позднее окончание входящих в него работ (секторыБиВ -обытий) равны:

5. Общий резерв времени каждой работы, как уже указывалось выше, равен:

Так как значение tf°-, при использовании этого метода, не опре­деляется, то его необходимо заменить на

Например, для работы 2 — 5: R2-5 = 13-2-6 = 5.

6. Частный резерв времени, как было показано ранее, равен разности между ранним началом последующих работ и ранним окон­чанием рассматриваемой работы:

Заменив, как в случае определения общего резерва, , получим окончательную формулу расчёта частного резерва времени рассматриваемым методом:

Например, для работы 2-6: =14-2-5 = 7.

Источник