Сетевая модель с расчетом по критическому пути

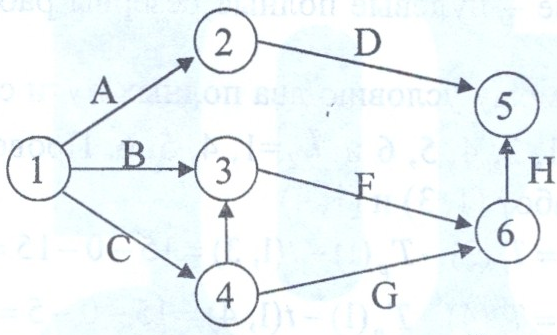
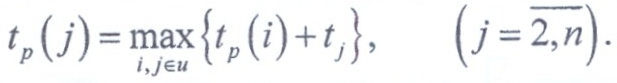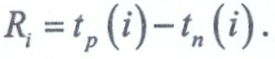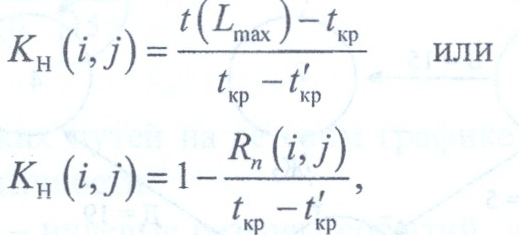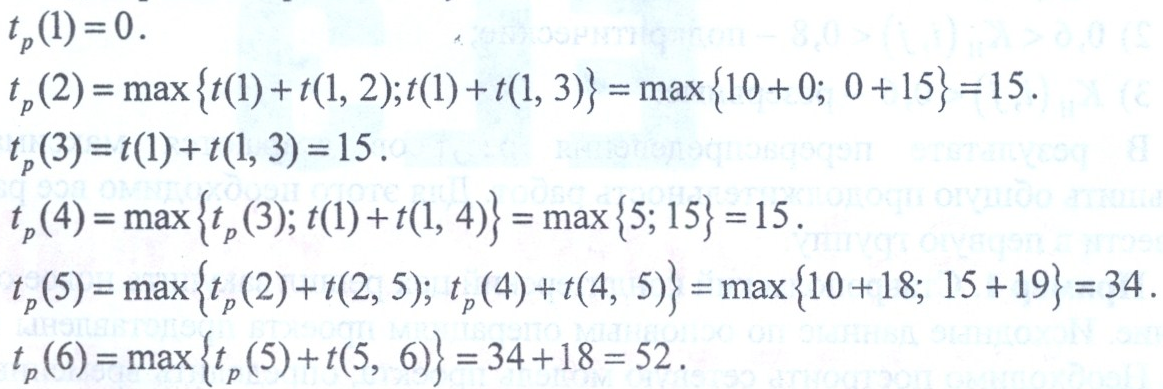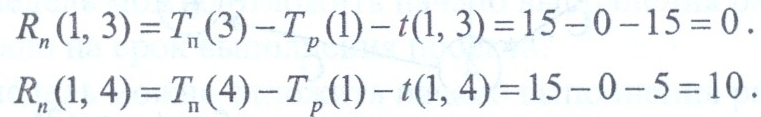2.2. Расчет временных параметров сетевого графика 2.2.1. Расчет критического пути

Почти в любой сети от исходного события до завершающего ведет несколько путей. Каждому пути соответствует последовательность каких-то работ. Путь в сети от исходного события до завершающего называется полным путем. Обозначается полый путь буквой L. Продолжительностью пути в сетевом графике называется время, необходимое для выполнения всех работ, лежащих на этом пути. Продолжительность полного пути обозначим t (L) .

Путь, имеющий наибольшую протяженность, называется критическим путем . Протяженность критического пути обозначаем t ( ) или .

Замечание. В сети может быть несколько критических путей.

Работы, лежащие на критическом пути, называются критическими. От их продолжительности зависит общий срок завершения всех работ. Некритические работы допускают некоторое запаздывание в их выполнении, которое не задержит сроков реализации всего проекта.

Ранним сроком (j) свершения события j называется самый ранний момент времени, к которому завершаются все предшествующие этому событию работы. Счет времени ведется от момента наступления начального события. Ранний срок начального события равен 0. (0) = 0. Ранний срок любого другого j-гo события определяется продолжительностью самого длительного из предшествующих путей. Определяем ранние сроки свершения событий по рекуррентному соотношению:

Полный срок наступления события — время, при котором планируемый срок окончания проекта не меняется. Обозначается (i) — для i-гo события.

Замечание. Для завершающего события К поздний срок наступления совпадает с ранним, т. е.

(К) = (К).

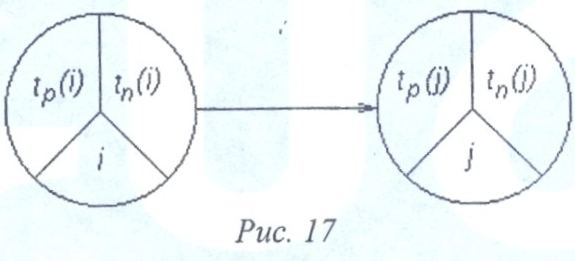
При определении поздних сроков наступления события расчет ведут от завершающего события к исходному. Каждую вершину орграфа (событие сетевой модели) разобьем на 3 сектора: в нижнем проставляем номер события; в левом — ранний срок; в правом — поздний срок.

Резервы времени каждого события находятся по формуле:

Замечание. Для событий i, лежащих на критическом пути, ранние и поздние сроки наступления совпадают, т. е. (i)= (i).

Понятие ранних и поздних сроков наступления событий играют важную роль в процессе выполнения проекта. Если все события i наступают не позднее (i), то это значит, что проект осуществится не позднее установленного срока.

Если какое-то событие i наступает позднее (i), то принимают меры для ускорения работ в этой части проекта. Если ускорить работу не удается, то полный срок выполнения проекта будет превышен. Время, на которое задерживаются все работы, можно тоже вычислить по сетевому графику.

Метод расчета сетевых графиков выполняется в четыре этапа:

1. Определение ранних сроков наступления событий (i)

2. Нахождение критического пути

3. Определение поздних сроков наступления события (i)

4. Определение резерва времени события.

Замечание. Использование независимого резерва времени на i-й работе, которая его имеет, не влияет на ранние и поздние сроки совершения всех событий и работ сети. Его нельзя передать ни предшествующим, ни последующим работам.

Оптимизация СМ выражается в перераспределении ресурсов с ненапряженных работ на критические для ускорения их выполнения. Для этого необходимо как можно более точно оценить степень трудности своевременного выполнения всех работ, а также всех «цепочек» пути. Более точным инструментом решения этой задачи, по сравнению с полным резервом, является коэффициент напряженности. Его можно вычислить по следующим формулам:

где t ( ) — продолжительность максимального пути, проходящего через работу (i, j);

— продолжительность отрезка рассматриваемого пути, совпадающего с критическим путем.

Коэффициент напряженности изменяется от 0 до 1. Чем ближе он к 1, тем сложнее выполнить данную работу в установленный срок.

Самыми напряженными являются работы критического пути, для которых = 1.

На основе этого коэффициента все работы сетевого графика подразделяются на три группы:

1) (i,j) > 0,8 — напряженные;

В результате перераспределения ресурсов стараются максимально уменьшить общую продолжительность работ. Для этого необходимо все работы перевести в первую группу.

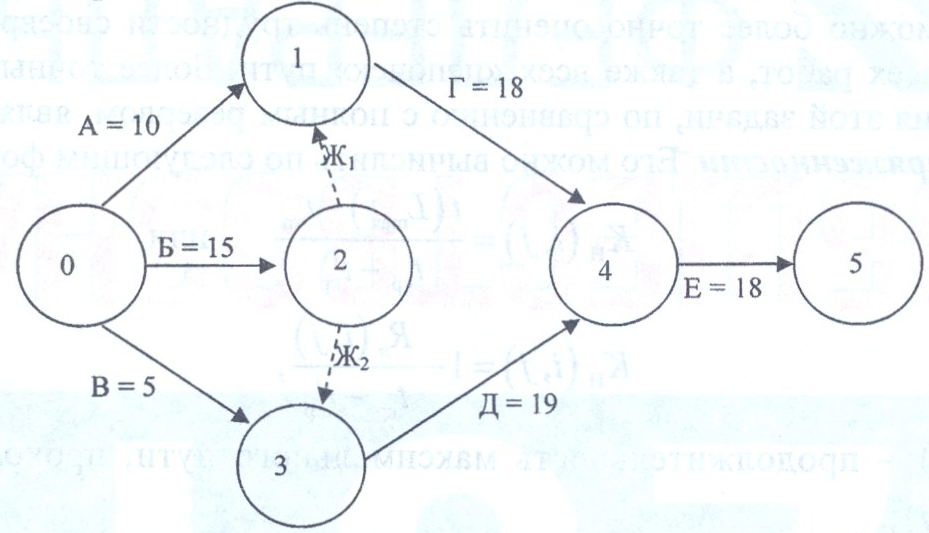
Пример 1. Ставропольский кондитерский цех решил закупить новое оборудование. Исходные данные по основным операциям проекта представлены в таблице. Необходимо построить сетевую модель проекта, определить временные параметры модели, критический путь и проанализировать, как влияет на ход выполнения проекта задержка определенного типа оборудования на 12 часов.

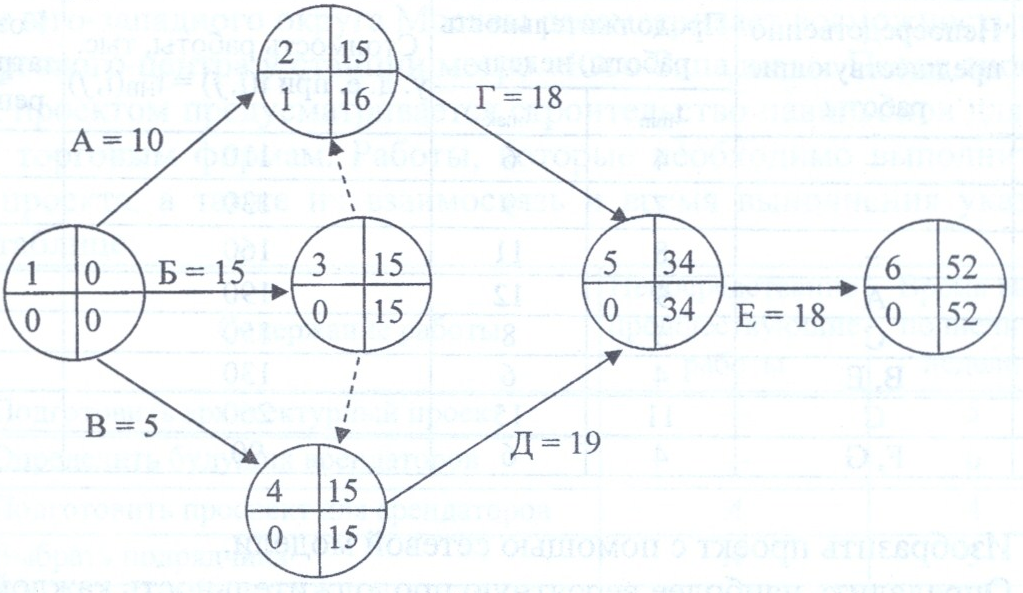
Решение. Построим сетевую модель по условию задачи.

Работы и введены для устранения параллельности работ Г и Д. Расчет критического пути включает два этапа. Первый называется прямым проходом. Вычисления начинают с исходного собьпия и продолжают до тех пор, пока не будет достигнуто завершающее событие. Для каждого события вычисляет одно число, представляющее ранний срок его наступления. На втором этапе, называемом обратным проходом, вычисления начинают с завершающего события и продолжают, пока не будет достигнуто исходное событие. Для каждого события вычисляется поздний срок его наступления.

Найдем ранние сроки наступления событий:

Найдем поздние сроки наступления событий для завершающего события 6 (6) = (6).

(5) = (6)-t (5, 6) = 52 -18 = 34.

(4) = (5) – t (4, 5) = 34-19 = 15.

(2) = (5) – t (2, 5) = 34 — 18 = 16.

(4) — t (1, 4)> =min = 0

При поиске критических путей на сетевом графике будем использовать следующие условия его критичности:

• необходимое условие — нулевые резервы событий, лежащих на критическом пути;

• достаточное условие — нулевые полные резервы работ, лежащих на критическом пути.

Согласно необходимому условию два полных пути сетевой модели могут быть критическими:

L₁ =1, 3, 4, 5, 6 и L₂ =1, 4, 5, 6. Проверим достаточное условие критичности для работ (1, 3) и (1, 4)

Путь L₂, начинающийся с работы (1, 4) не является критическим, так как минимум одна (1, 4) из его работ не является критической. Работа (1, 4) имеет не нулевой полный резерв, а значит, может быть задержана с выполнением, что недопустимо для критических работ.

Таким образом, сетевая модель имеет единственный критический путь ,=1, 3, 4, 5, 6, длительностью

= 52 часа. За выполнением работ этого пути необходим особый контроль, так как любое увеличение их длительности нарушит срок выполнения проекта в целом.

Работа А или (1, 2) не является критической, ее полный резерв равен 1 часу.

Это означает, что при задержке работы в пределах 1 часа срок выполнения проекта не будет нарушен. Поэтому, если согласно условию работа А задержится на 12 часов, то весь проект задержится на 11 часов.

Пример 2. Компания «АВC» реализует проекты серийного производства различных видов продукции. Каждый проект обеспечивает получение в неделю 100 тыс. у. д. е. дополнительной прибыли. Перечень работ и их характеристики представлены в таблице.

1. Изобразить проект с помощью сетевой модели.

2. Определить наиболее вероятную продолжительность каждой работы.

3. Найти все полные пути сетевого графика, определить критический путь, ожидаемую продолжительность выполнения проекта и полную стоимость всех работ.

Решение. Построим сетевую модель проекта:

2. Наиболее вероятная продолжительность работ

t_HB = (2t_min + 3t_max)/5.

t_{НВ А} = (2·4 + 3 · 6)/5 = 5,2

t_{НВ В} = (2 · 7 + 3 · 9)/5 = 8,2

t_{НВ С}= (2′ 8 + 3 ·11)/5= 9,8

t_{НВ D}= (2· 9 + 3 · 12)/5 = 10,8

t_{НВ Е} = (2 · 5 + 3 · 8)/5 = 6,8

t_{НВ F}= (2·4 + 3 · 6)/5 = 5,2

t_{НВ G}= (2· 11 + 3 · 15)/5 = 13,4

t_{НВ Н} = (2 · 4 + 3 · 6)/5 = 5,2

Источник

Критический путь

Путь – любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующий за ней работы.
Полный путь L – любой путь, начало которого совпадает с исходным событием сети, а конец – с завершающим.
Наиболее продолжительный полный путь в сетевом графике называется критическим. Критическими также называются работы и события расположенные на этом пути. Работы этого пути определяют общий цикл завершения всего комплекса работ, планируемых при помощи сетевого графика. И для сокращения продолжительности проекта необходимо в первую очередь сокращать продолжительность работ, лежащих на критическом пути.

1. Составить экономическое содержание задачи и перечислить перечень работ.
2. Построить сетевой график и определить критический путь.
3. Рассчитать параметры сетевого графика и поздние сроки поступления событий, резервы времени.

Работа (i,j)	Количество предшествующих работ	Продолжительность tij	Ранние сроки: начало tij Р.Н.	Ранние сроки: окончание tij Р.О.	Поздние сроки: начало tij П.Н.	Поздние сроки:окончание tij П.О.	Резервы времени: полный tij П	Резервы времени: свободный tij С.В.	Резервы времени: событий Rj
(1,2)	0	3	0	3	1	4	1	0	1
(1,3)	0	6	0	6	0	6	0	0	0
(1,4)	0	4	0	4	9	13	9	9	0
(2,3)	1	2	3	5	4	6	1	1	0
(2,5)	1	5	3	8	12	17	9	2	7
(3,4)	2	7	6	13	6	13	0	0	0
(3,5)	2	4	6	10	13	17	7	0	7
(3,6)	2	4	6	10	15	19	9	9	0
(4,6)	2	6	13	19	13	19	0	0	0
(5,6)	2	2	10	12	17	19	7	7	0

Критический путь: (1,3)(3,4)(4,6)
Продолжительность критического пути: 19 Перейти к онлайн решению своей задачи Пример . Рассчитать параметры сетевого графика мероприятия по совершенствованию системы управления. Сетевая модель задана таблично. Продолжительность выполнения работ дана в виде минимальной и максимальной оценок. Требуется вычислить табличным методом все основные характеристики работ и событий, найти критический путь и его продолжительность.
Скачать

Источник

8.3. Расчет сетевой модели

Расчет параметров может вестись различными методами (аналитическими, в табличной форме, по графику) вручную или с применением компьютеров.

Рассмотрим пример (рис.4.) расчета сетевого графика табличным методом. Продолжительность критического пути определяется при рассмотрении всех путей последовательно выполняемых работ от исходного события до конечного (табл.1).

3

3

1 1 3

2

Рис.4. Схема сетевого графика

Расчет критического пути по сетевому графику

Суммирование продолжительности работ по путям сетевого графика

Суммирование продолжительности работ по путям сетевого графика

Из табл.1 видно, что наибольшую продолжительность имеет цепочка работ, ограниченная событиями 1,2,5,6,8. Она равна 16 дн. (или в других единицах времени).

Рассмотрим на примере одной работы определение других параметров сетевого графика.

Раннее начало работы – это самый ранний из возможных сроков начала работы с учетом сроков выполнения предшествующих работ.

Раннее начало работы определяется продолжительностью самого длинного пути от начального события до начала работы по формуле

где ∑ t_{h-і ,} — максимальная продолжительность всех работ от начального события до начала данной работы.

Раннее окончание работы – это срок окончания работы при условии ее начала в самый ранний из возможных сроков. Раннее окончание работы определяется путем суммирования раннего начала и продолжительности данной работы по формуле

Позднее начало работы – это самый поздний срок, при котором может быть начата работа без нарушения продолжительности критического пути, т.е. общего срока выполнения программы.

Позднее начало определяется разностью критического пути и суммы продолжительности данной работы и самого длинного пути от конечного события до события, стоящего у конца данной работы, по формуле

где ∑ t_ј-k — максимальная продолжительность от завершающего события до окончания данной работы.

Позднее окончание работы – это предельно допустимый срок, в который может быть окончена данная работа без увеличения продолжительности критического пути. Позднее окончание равно сумме позднего начала и продолжительности данной работы и определяется по формуле

После расчета ранних и поздних начал и окончаний можно определить резервы времени, которые имеются при выполнении отдельных работ при общей продолжительности строительства, равной критическому пути.

Общий запас времени – это время, на которое можно перенести начало работы или увеличить ее продолжительность, не нарушая общего срока выполнения программы. Общий запас определяется разностью позднего и раннего начала или позднего и раннего окончания работ по формулам:

Частный запас времени – это время, на которое можно перенести начало работы или увеличить ее продолжительность без изменения раннего начала последующих работ. Частный запас определяется как разность раннего начала последующей работы и раннего окончания данной работы

где t_і-k — раннее начало последующей работы; t_і-ј — раннее окончание данной работы.

Расчет начинается с записи в табл.2 перечня работ и их продолжительности

Результаты расчета сетевого графика

Источник