31. Сетевая модель, сетевой график. Временные параметры сетевого графика и порядок их расчета.
Сетевые модели впервые примененные в 1958 г., наилучшим образом описывают выполнение самых сложных строительных и любых других комплексов работ. Для любой задачи управления характерна множественность ее решений. Кроме того, постоянное усложнение техники и технологии строительного производства и связанное с ним усложнение процесса управления делают выбор оптимального решения чрезвычайно трудным.
Модель представляет собой абстрактное отображение наиболее существенных характеристик, процессов и взаимосвязей реальных систем. Модель — это условный образ объекта, сконструированный для упрощения его исследования.
Модель представляет собой абстрактное отображение наиболее существенных характеристик, процессов и взаимодействий реальных систем. Для сетевого планирования используется сетевая модель. Она изображается в виде графика, состоящего из стрелок и кружков.
Сетевой график представляет собой сетевую модель с рассчитанными временными параметрами. В основе построения сети лежат понятия «работа» и «событие», «ожидание», «зависимость», и «критический путь(полный путь, имеющий наибольшую длину (продолжительность) из всех полных путей)».
Работа – производственный процесс, требующий затрат времени и материальных ресурсов, приводящий к достижению определённых результатов.
Событие – факт окончания одной или нескольких работ, необходимый и достаточный для начала следующих работ. События ограничивают работу и по отношению к ней могу быть начальными(определяет начало данной работы и является конечным для предшествующей работы) и конечными(окончание данной работы и является началом для последующей).
Исходное событие – событие, которое не имеет предшествующих работ, в рамках рассматриваемого сетевого графика.
Завершающее событие – не имеет последующих работ, в рамках сетевого графика.
Сложное событие – событие, в которое входит или из которого выходит 2 или более работы.
Зависимость – фиктивная работа(вводиться для отражения технологической и организационной взаимосвязи работ и не требует ни времени ни ресурсов).
Ожидание – технологический и организационный перерыв между работами, требующий только затрат времени.
Путь – непрерывная последовательность работ в сетевом графике.
Путь от исходного к завершающему событию – полный путь.
Критический путь – полный путь, имеющий наибольшую продолжительность из всех полных путей от начального события до завершающего.
Основные методы расчета сетевых графиков: расчет сети непосредственно на графике, расчет сетевого графика табличным методом, расчет сетевого графика по потенциалам событий и др.
Расчет сети непосредственно на графике. Расчет непосредственно на графике является самым простым и быстрым из ручных способов. При этом способе расчета строгое соблюдение правила кодирования событий не обязательно.
1 . У исходного события под чертой (в знаменателе) ставят нуль.
2. Для каждого следующего события в знаменателе записывают число, равное сумме значения раннего срока свершения предыдущего события и продолжительности работы.
3. Если в событие входит две работы или больше, то рассчитывают значение каждой из них, записывая над стрелкой, но в знаменатель переносят только максимальное значение из всех полученных.
4. В завершающем событии значение, записанное в знаменатель, определяющее длину критического пути, переносят над чертой (в числитель).
5. Значение числителей определяют, ведя расчет от завершающего события к исходному, вычитая из значения поздних сроков свершения конечного события продолжительность предшествующих им работ. В отличие от расчета ранних сроков (знаменатель), если из события выходят две работы или более, принимают не максимальное, а минимальное значение.
6. Критический путь проходит через события, в которых значения в числителе и знаменателе совпадают. Полный и частный резерв времени для работ критического пути равен нулю.
7. Общий резерв времени для любой работы определяют вычитанием из значения числителя (конечного события данной работы) суммы значений знаменателя (начального события данной работы) и ее продолжительности.
8. Частный резерв для любой работы определяют вычитанием из значения знаменателя конечного события данной работы суммы значений знаменателя начального события и продолжительности данной работы.
Расчетные параметры сетевого графика:
i-j — код данной работы (определяются на основе сетевого графика (первая цифра — начало стрелки, вторая — конец), а продолжительности указаны над стрелками).
i — код начального события данной работы
j- код конечного события данной работы
h-i — код работ, предшествующих данной работе
h — код событий, предшествующих начальному событию данной работы
j-k — код работ, последующих за конечным событием данной работы
k — код событий, последующих конечному событию данной работы
Lкр. — критический путь (Критическим путем называют полный путь, имеющий наибольшую длину (продолжительность) из всех полных путей. При расчёте критического пути непосредственно на графике, критический путь проходит через события, в которых значения в числителе и знаменателе совпадают. Полный и частный резерв времени для работ критического пути равен нулю).
ТL- продолжительность пути
ТLкр. — продолжительность критического пути или критический срок
ti-j- продолжительность работы
Ti-jр.н. — раннее начало работы (это самый ранний из возможных сроков начала работы с учетом сроков выполнения предшествующих работ. Раннее начало работы определяется продолжительностью самого длинного пути от начального события до начала данной работы).
Ti-jр.о.- раннее окончание работы (это срок окончания работы при условии ее начала в самый ранний из возможных сроков. Раннее окончание работы определяется путем суммирования раннего начала и продолжительности данной работы)
Tiр — ранний срок свершения события i
Ti-jп.н. — позднее начало работы i-j (это самый поздний срок, при котором может быть начата работа без нарушения продолжительности критического пути, т. е. общего срока выполнения программы. Позднее начало определяется разностью критического пути и суммы продолжительности данной работы и самого длинного пути от конечного события до события, стоящего у конца данной работы).
Ti-jп.о. — позднее окончание работы i-j (это предельно допустимый срок, в который может быть окончена данная работа без увеличения продолжительности критического пути. Позднее окончание равно сумме позднего начала и продолжительности данной работы).
Т j» — поздний срок свершения события j
R i-j — общий (полный) резерв времени работы i-j (это время, на которое можно перенести начало работы или увеличить ее продолжительность, не нарушая общего срока выполнения программы. Общий запас определяется разностью позднего и раннего начала или позднего и раннего окончания работ).
r i-j — частный (свободный) резерв времени работы i-j (это время, на которое можно перенести начало работы или увеличить ее продолжительность без изменения раннего начала последующих работ. Частный запас определяется как разность раннего начала последующей работы и раннего окончания данной работы)
Правила построения сетевых графиков
Для построения сетевого графика необходимо выявить последовательность и взаимосвязь работ: какие работы необходимо выполнить, и какие условия обеспечить, чтобы можно было начать данную работу, какие работы можно и целесообразно выполнять параллельно с данной работой, какие работы можно начать после окончания данной работы. Эти вопросы позволяют выявить технологическую взаимосвязь между отдельными работами, обеспечивают логическое построение сетевого графика и его соответствие моделируемому комплексу работ.
Уровень детализации сетевого графика зависит от сложности строящегося объекта, количества используемых ресурсов, объёмов работ и продолжительности строительства.
Имеется два типа сетевых графиков:
Сетевые графики типа «вершины — работы».
Элементами такого графика являются работы и зависимости. Работа представляет собой определенный производственный процесс, требующий затрат времени и ресурсов для его выполнения, и изображается прямоугольником. Зависимость (фиктивная работа) показывает организационно-технологическую связь между работами, не требующую затрат времени и ресурсов, изображается стрелкой. Если между работами имеется организационный или технологический перерыв, то на зависимости указывается длительность этого перерыва. Пример сетевого графика «вершины — работы» приведен на рис. 6.1.
Рис. 6.1. Сетевой график типа «вершины — работы»
Если работа сетевого графика «вершины — работы» не имеет предшествующих работ, то она является исходной работой этого графика. Если работа не имеет последующих работ, то она является завершающей работой сетевого графика. В сетевом графике «вершины — работы» не должно быть замкнутых контуров (циклов), т.е. зависимости не должны возвращаться в ту работу, из которой они вышли.
Сетевые графики типа «вершины-события».
Элементами такого типа графиков являются работы, зависимости и события. Работа изображается сплошной стрелкой, зависимость – пунктирной. Событие представляет собой результат одной или нескольких работ, необходимый и достаточный для начала одной или нескольких последующих работ, и изображается кружком.
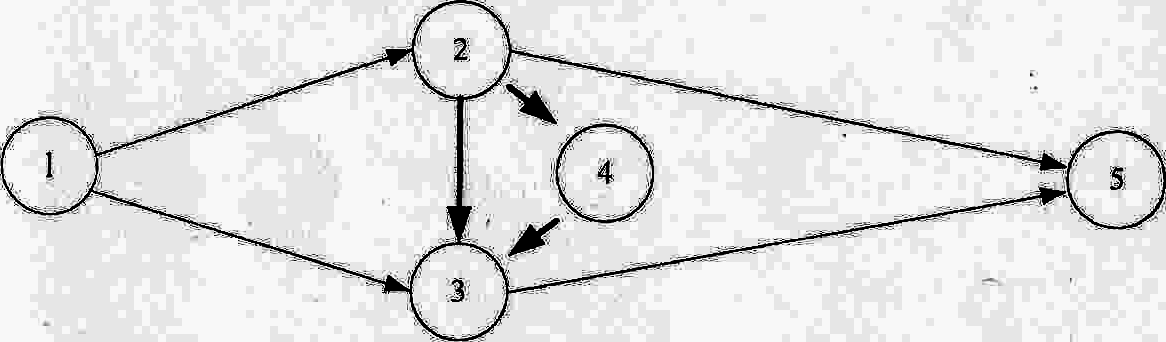
В сетевых графиках этого типа каждая работа находится между двумя событиями: начальным, из которого она выходит, и конечным, в которое она входит. События сетевого графика нумеруются, поэтому каждая работа имеет код, состоящий из номеров её начального и конечного события. Например, на рис. 6.2 работы закодированы как (1,2); (2,3); (2,4); (4,5).
Рис.6.2. Сетевой график «вершины — события»
Если событие сетевого графика «вершины-события» не имеет предшествующих работ, то оно является исходным событием этого графика. Следующие непосредственно за ним работы называются исходными. Если событие не имеет последующих работ, то оно является завершающим событием. Входящие в него работы называются завершающими.
Для правильного отображения взаимосвязей между работами необходимо соблюдать следующие основные правила построения сетевого графика «вершины-события»:
1. При изображении одновременно или параллельно выполняемых работ (например, работ «Б» и «В» на рис.6.2) вводятся зависимость (3,4) и дополнительное событие (3).
2. Если для начала работы «Г» необходимо выполнить работы «А» и «Б», а для начала работы «В» – только работу «А», то вводится зависимость и дополнительное событие (рис.6.3.).
Рис.6.3. Изображение зависимости между работами
3. В сетевом графике не д.б. замкнутых контуров (циклов), т.е. цепочки работ, возвращающейся к тому событию, из которого они вышли (рис.6.4).
Рис. 6.4. Пример замкнутого контура (2,4,3,2)
4. В сетевом графике при поточной организации строительства вводятся дополнительные события и зависимости (рис. 6.5.).
Рис. 6 5. Пример изображения потоков однородных работ