Сетевая модель социальной сети

Алексей Савватеев: Модели интернета и социальных сетей

В 2013 году Алексей Савватеев прочитал несколько лекций по моделям соцсетей и интернета. Я нашел эту тему очень любопытной и незаслуженно забытой. Попробуем разобраться в вопросе. А ещё мне интересно узнать, как изменилась ситуация с тех пор и какие полезные публикации есть в этой области.

И в интернете, и в биологии соцсети проявляют свойства, которые по отдельности описываются моделями, но все вместе — ставят в тупик современную математику. Савватеев утверждает, что «тот, кто с этим разберется получит Нобелевскую премию». Будущее будет зависеть от способности работать с сетями.

Ниже приводится скомпилированная выжимка из трёх видеозаписей лекций, само видео есть в конце. (Пост выглядит как набор слайдов с цитатами лектора, связать всё в единый и прилизанный текст у меня не хватает способностей к русскому языку и математике, но тема очень важная, поэтому хочу опубликовать.)

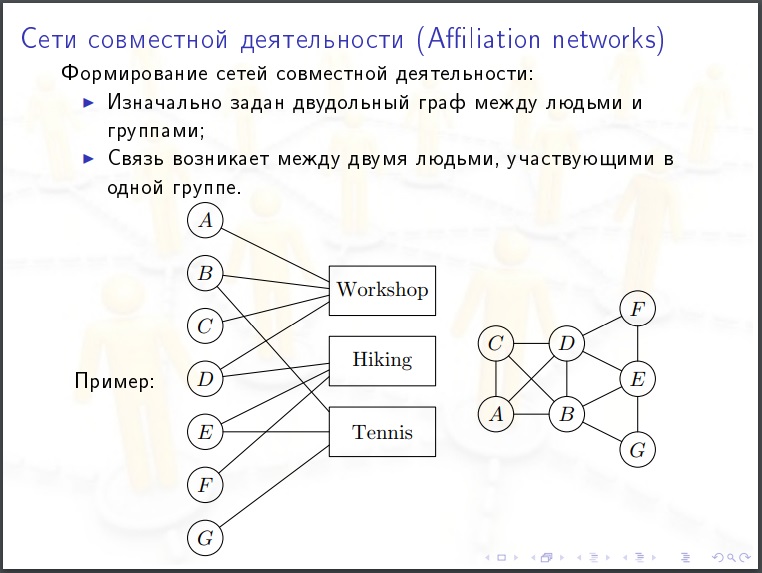
Социальная сеть состоит из:

Было бы честно строить модель взвешенных графов, когда указаны коэффициенты «силы связи». Но нам до этого как до Луны.

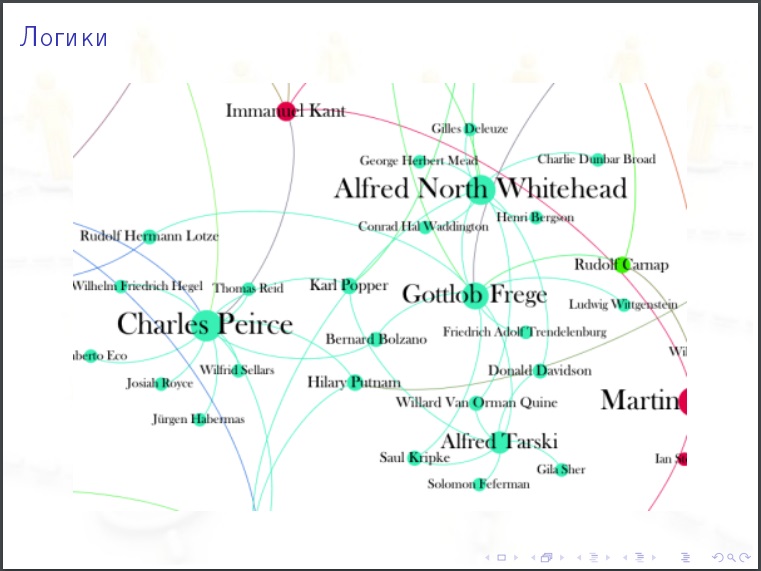
Галерея

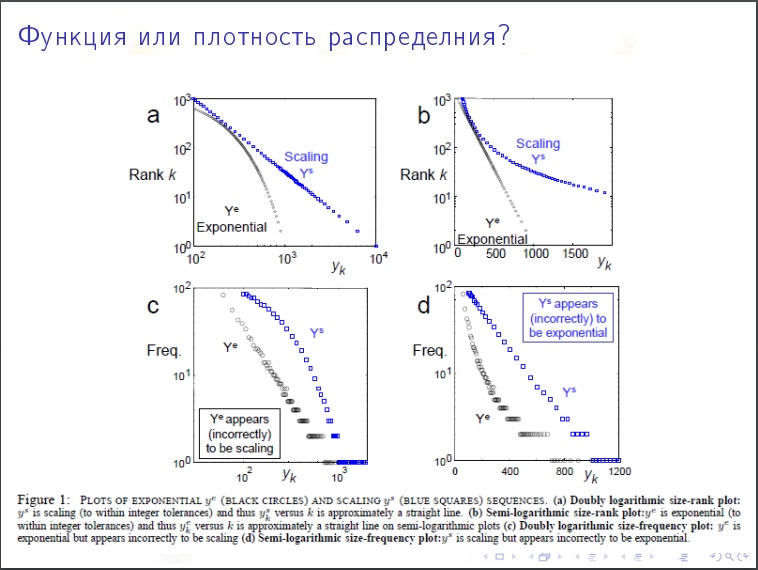
На картинки полезно смотреть. Гипотезу, которую вы могли бы выдвинуть, после просмотра картинки может оказаться очевидно абсурдной.

Кому полезно изучать соцсети

Экономика: Есть предположение, что микро и макро уровень в экономике связаны через «сеть»
Политология: Есть предположение, останется ли режим или поменяется, зависит от того, у кого будут более сильные специалисты по сетям.

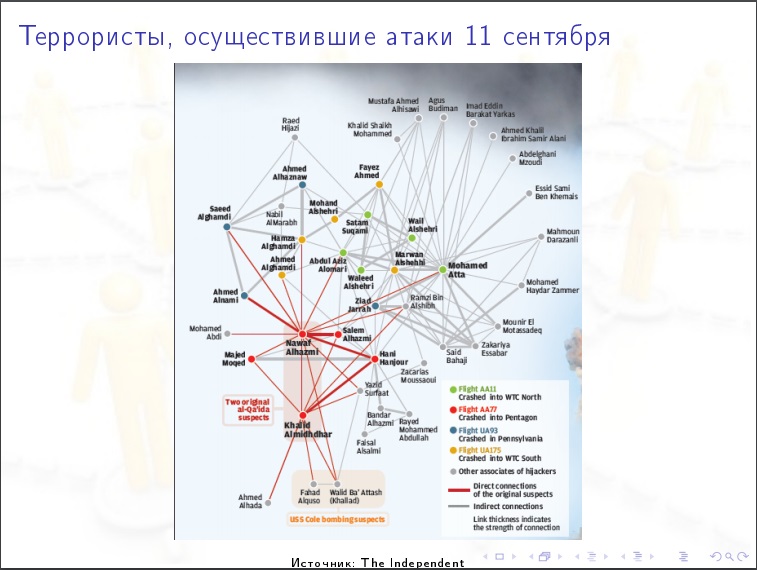
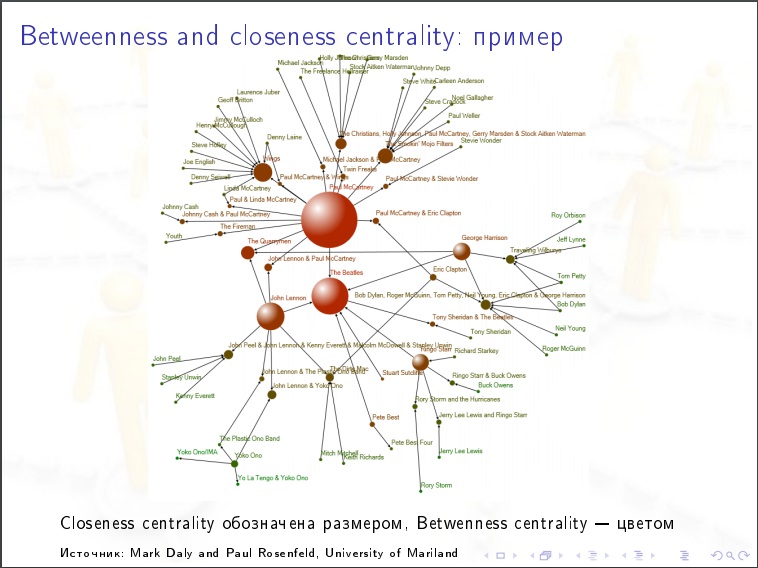
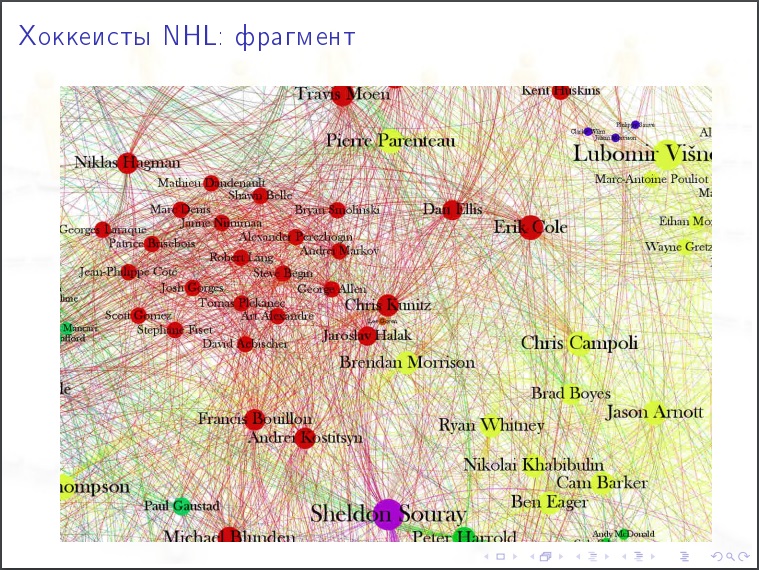
Пример аналитики соцсетей.

Численные характеристики социальных сетей

• Расстояние
• Диаметр
• Степень вершины
• Распределение степеней вершины
• Меры центральности узла
• Распределение меры центральности
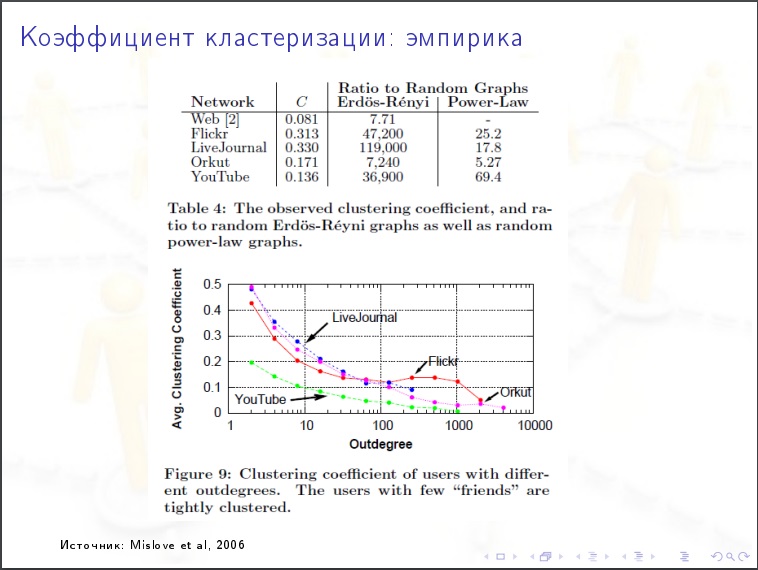
• Коэффициент кластеризации
• Коэффициент ассортативности

Расстояние — сколько рёбер минимально нужно пройти, чтобы попасть от одной вершины к другой.

Диаметр — максимальное расстояние в графе.

Степень вершины — количество рёбер у вершины.

Теория шести рукопожатий

Любой социальный граф имеет очень низкий средний диаметр (Теория шести рукопожатий). Причем существует очень плотное ядро. Я «знаком» с каким-нибудь африканцем, через своего президента, который жал руку африканскому президенту.

Локальный коэффициент кластеризации. Мы смотрим всех соседей человека, «к» штук. Максимум ребер — к(к-1)/2. Мы смотрим на фактическое число ребер и делим на этот максимум.

Глобальный коэффициент кластеризации. Сколько «треугольников» по сравнению с «галочками».

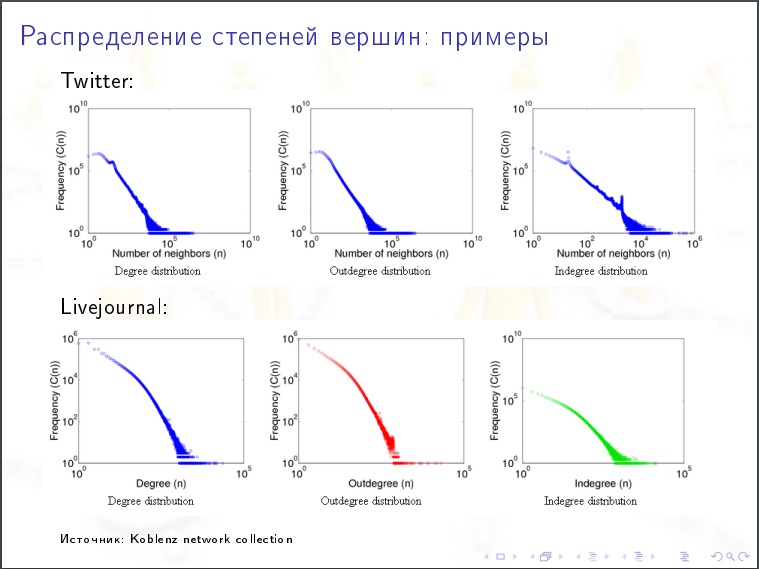
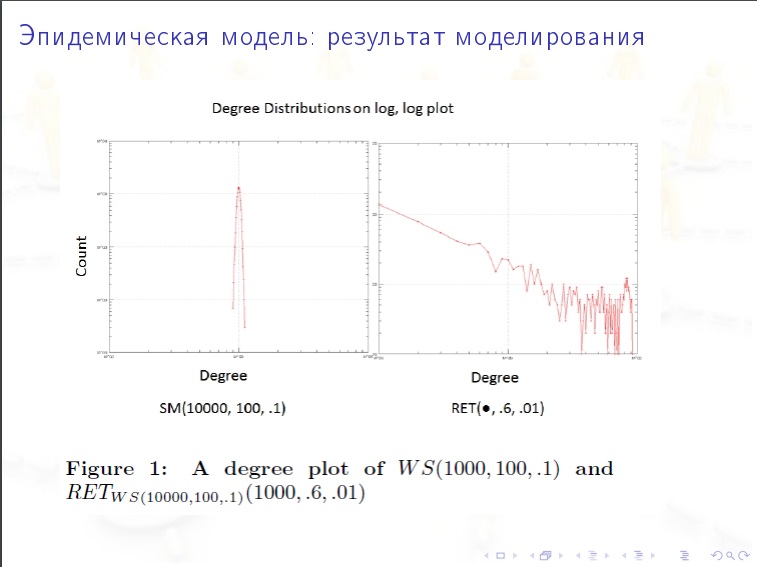
Распределение степеней вершины. Какой % вершин имеет степени меньше 1000? Природа распределения экспоненциальная или степенная? Выясняется что у интернета степенная природа.

Коэффициент равен «2». Вершин, степень которых равна «х», будет N/х 2 . Проверяем, в ЖЖ миллиард пользователей, тысячников должно быть миллиард разделить на тысячу в квадрате. Тысяча тысячников.

Это очень медленно убывающая штука.

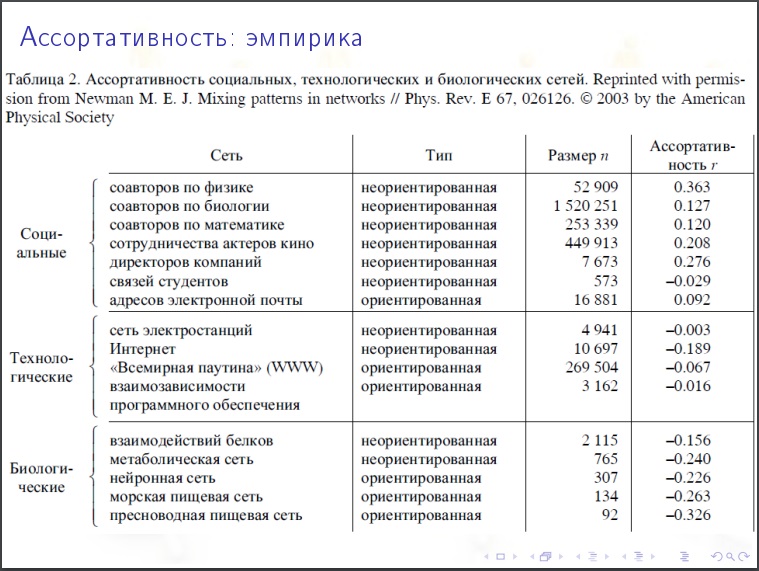
Коэффициент ассортативности. грубый подход — берем вершины с примерно одинаковым количеством степеней, они с большей вероятностью с друг другом связаны или с меньшей? Если да — то ассортативны. Диссортативность — когда с большим количеством степеней вероятнее связаны с меньшим. Это наивный подход. Более правильный подход такой. В каждой вершине есть еще какая-то характеристика (общий капитал банка) и смотрится ассортативность по этому показателю.

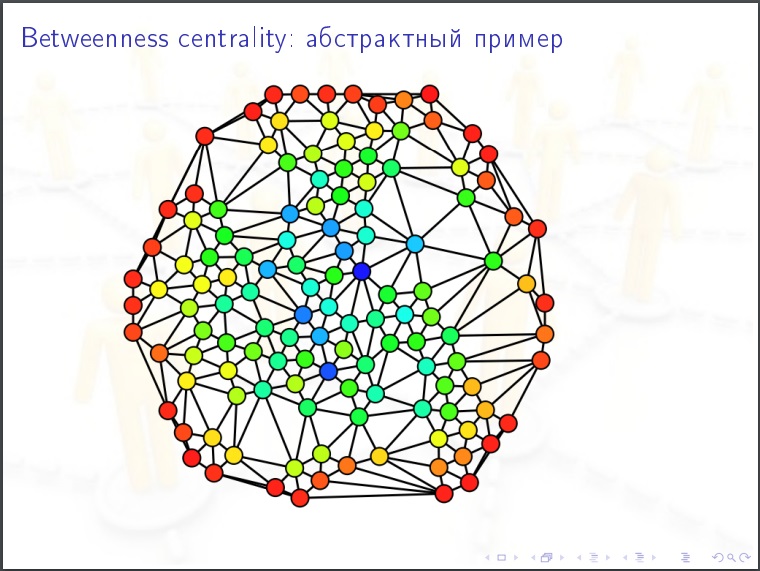
Центральность узла для социальной сети. Берем человека, считаем для него следующую величину. Перебираем все пары остальных людей (N-1)(N-2)/2 и в каждом случае спрашиваем, ближайший путь знакомств в графе, проходит ли через этого человека? Может быть несколько кратчайших путей и некоторые из них содержат нашего человека, тогда ставим ему %. Это важнейшая характеристика в социальных сетях. Для распространения эпидемий, общественных мнений. Это то что надо измерять.

Особенности социальных сетей:

• Маленький диаметр и среднее расстояние между вершинами
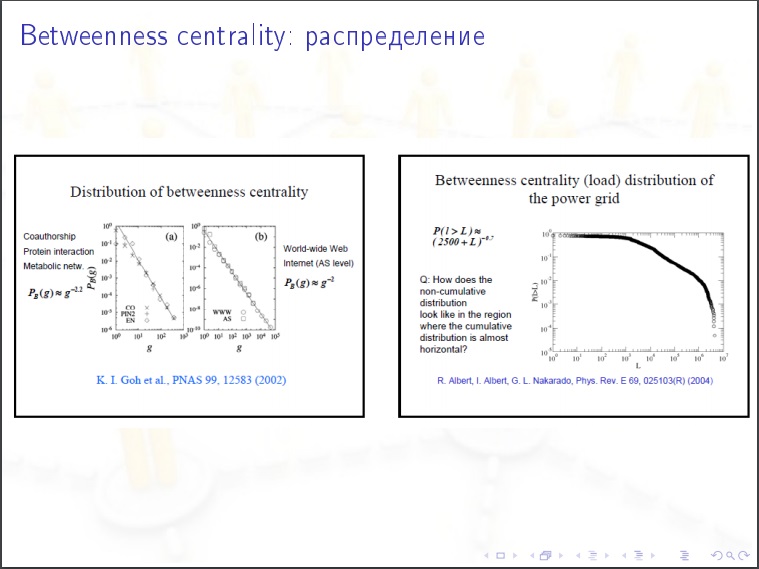
• Степенной закон распределения степеней вершин и betweenness centrality
• Высокий коэффициент кластеризации
• Ассортативность
• Наличие тесно связанного ядра

Задача — создать модель, которая охватывает первые три свойства (а желательно и последние два). Первые три уже представляют непреодолимую сложность на данный момент времени. На 2013 год не существует такой модели.

Перейдем к описанию моделей случайных графов которые существовали.

Модели

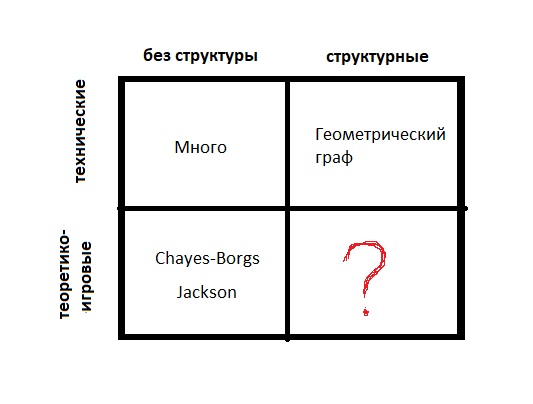
• Технические (ребра получаются случайным образом)
• Теоретико-игровые (когда это кому то выгодно)
• Без структуры (просто множество вершин)
• Структурные (вершины являются точками метрического пространства или имеют веса, на множестве вершин имеется структура)

Если вы понимаете, что лежит в основе, вы можете руководствоваться очень большим числом параметров. Если хорошо подобранные параметры дадут хорошую аппроксимацию, то вы молодец. А если даже самая лучшая комбинация дает плохой результат и не согласуется с наблюдаемыми фактами, то до свидания.

Всё это делается для одной цели — бороться со спамом.

Интернет можно представить как сложную сеть на нескольких уровнях:

• Технологический уровень. Вершинами и рёбрами являются узлы и линии связи.
• Гипертекстовый уровень. Вершинами являются сайты или страницы, а рёбрами — гиперссылки.
• Социальный уровень. Вершинами являются пользователи, а рёбрами – те или иные связи между ними: дружба в социальных сетях, подписка на блоги, совместная работа в распределённых проектах (напр., википедия) и т.п.

Для сложных сетей известно множество локальных и глобальных числовых характеристик: распределение степеней вершин, коэффициент кластеризации, коэффициент ассортативности

Выясняется, что для интернет-сетей характерен ряд особенностей:

• паретто-распределение степеней,
• высокий коэффициент кластеризации,
• положительная ассортативность,
• маленький диаметр.

Конечной целью моделирования интернет-сетей является построения модели с теми же особенностями.

Модель Эрдёша — Реньи

Модель Эрдёша — Реньи — это одна из двух тесно связанных моделей генерации случайных графов. Модели названы именами математиков Пала Эрдёша и Альфреда Реньи, которые первыми представили одну из моделей в 1959 году. Исследовали граф знакомств.

Рассмотрим N точек. Потенциальных рёбер — N*(N-1)/2. Для каждого ребра мы проводим случайное испытание. Вероятность того, что ребро случилось — р. Что не случилось — (1-р). Поводим «испытания», получается граф. Но есть несколько проблем. Чтобы проявилось свойство «разреженности», р должно быть очень маленьким, порядка 1/N, а тогда диаметр будет очень большим.

Любой исследователь, который услышит, что интернет описывается как случайный граф по модели Эрдёша — Реньи будет ржать.

Интересный эффект — при преодолении некоего порога вероятности, граф становится связным.

Модель Боллобаши

Это динамическая модель построения интернета. Мы пытаемся угадать как он постепенно формировался. Идея такая. Берем граф с одной вершиной и одним ребром, а дальше на каждом шаге разыгрываем случайным образом. Мы добавляем одну вершину, после этого, с некоторой вероятностью она замыкается на себя, а с некоторой вероятностью соединяется с предыдущей. Следующая вершина с некоторой вероятностью замыкается на себя, а с некоторой идет к одной из предыдущих. При этом вероятность попадания в вершину всегда пропорционально тому количеству рёбер, которые есть. Разыгрывается случайная величина, а следующий розыгрыш зависит от результата предыдущего. Такая модель интуитивно понятна, но математически сложно рассчитывать. Эта модель дает не экспоненциальное, степенное распределение. Диаметр совпадает.

Но эта модель не срабатывает с кластеризацией.

Есть два конкурирующих подхода, которые работают с кластеризацией.

Геометрический подход

Предположение берется с потолка. В основе графа интернет лежит метрическое пространство. Пространство вкусов, интересов, предпочтений. Насколько люди друг другу интересны. Насколько близки по духу, по взглядам. Если люди близки, они друг на друга ссылаются.

Мы берем и накидываем в это пространство 10 10 точек. Здесь появляется огромное количество параметров. Огромное.

Кластеризация отличная, но убывание вершин — экспоненциальное. Противоречие.

Этот метод страшно простой и алгоритмы делаются «на авось».

Теоретико-игровой подход Чайес-Боргса

Знали ли вы, что во времена фон Неймана было объявлено, что теория игр будет оружием нового поколения против Советского Союза?

Мы исходим из того, что люди принимают решения общаться с друг другом или нет.

Организуем встречи/события. Событие — это список приглашенных гостей, а так же его «интенсивность».
Издержки = Интенсивность * (константа + K*(количество приглашенных)). Я должен потратить ресурсы, чтобы мероприятие «продавить» и должен потратить ещё на каждого участника. Бывают дни рождения, а бывают походы. Появляется коэффициент «П», который маленький для дня рождения и большой для похода. Интенсивность знакомства.

Человек может организовать несколько событий с интенсивностями П₁, П₂… П_n. Другие делают так же.

Есть мои действия по налаживанию социальных связей, а есть чужие.

Функция выигрыша = (количество людей с которыми ты стал достаточно хорошо знаком) — издержки

«Достаточно хорошо знаком» — значит сумма интенсивностей всех событий где вы были вместе, больше некоторого порогового значения. Причем не важно, кто организовывал событие.

Ребра проводятся для достаточно хороших знакомств.

Доказано, что очень многие свойства реального замыкания получаются в этой модели. Во всех равновесиях Нэша выполняется свойства реального замыкания и даже более сильные свойства кластеризации, так же наблюдаемых на графе реального Интернета.

Но про остальные свойства ничего не понятно, но это пол беды. Беда в том, что если существует хоть одно равновесие Нэша, где хотя бы два человека друг друга знают, то существует равновесие Нэша, в котором все знакомы со всеми.

Есть идея совместить два подхода. Считать, что люди живут в метрическом пространстве, а когда организуют события, или участвует в событии, коэффициенты издержек, интенсивности и пороговое значение зависят от «близости». Это пятое поколение моделей.

Дифференцированные издержки

Варианты — сделать дифференцированные издержки и дифференцированные выигрыши. Одних проще пригласить, чем других. Знакомство с одним выгоднее, чем знакомство с другим.

Допустим, мы расположим всех людей равномерно по окружности. И вам пригласить дешевле того, кто ближе. Как будет выглядеть равновесие? Каждый пригласит некоторую окрестность, правда? Не правда. Такого равновесия не существует.

Доказательство. Предположим, что оно существует, тогда близкие друг к другу люди уже приглашены на много разных собраний. Тогда ему нет нужды приглашать этого близкого. Существование этого равновесия входит в противоречие с существованием этого равновесия.

Чистое равновесие существует, оно найдено, оно единственное. Каждый приглашает окрестность, которая лежит по (или против) часовой стрелки на некотором расстоянии от него и некоторой длины.

( — Это образование галактик!)
( — Это спонтанное нарушение симметрии!)

Выводы

Пелевин как то написал, что «смысл русского бытия в неспешном золочении безмерного иконостаса». Вот смысл математики — в том же самом. Только иконостас — научный.

Это в высшей степени мультидисциплинарное исследование. Высшее, насколько можно себе представить.

Источник