Зависимый резерв времени работы r3(I,j)
Поскольку резерв времени пути Liможет быть использован для увеличения цикла работ, находящихся на этом пути, можно сказать, что любая из работ пути Liна его участке, не совпадающем с критическим путем, обладает резервом времени. Но у этого резерва есть особенность: если мы его используем частично или целиком для увеличения цикла t(i,j) какой-либо работы (i,j), то соответственно уменьшается резерв времени у остальных работ Li. Поэтому такой резерв времени пути, на котором она находится, называется зависимым резервом времени работы (i,j) и обозначается через R3(i,j).
Независимый резерв времени работы Rн(I,j)
У отдельных работ помимо зависимого резерва времени может иметься и независимый резерв времени, обозначаемый черезRн(i,j). Он образуется в том случае, когда циклы работ (i,j) меньше, чем разность между наиболее ранним из возможных сроков свершения непосредственно следующего за данной работой события j и наиболее поздним из допустимых сроков свершения непосредственно предшествующего ей события i:
Свободный резерв времени работы (Rcij)
Свободный резерв времени работы (Rcij) — это разность между ранними сроками наступления событий i и j за вычетом продолжительности работы t(i,j):
Свободный резерв времени работы — максимальный период времени, на который можно увеличить продолжительность или отсрочить ее начало, не изменяя при этом ранних сроков последующих работ, при условии, что начальное событие этой работы наступило в свой ранний срок.
Возможности смещения сроков начала и окончания каждой работы определяется с помощью ранних и поздних сроков наступления событий, между которыми выполняется данная работа:
Анализ и оптимизация сетевой модели
Первоначально разработанная сетевая модель обычно не является лучшей по срокам выполнения работ и использования ресурсов. Поэтому исходная сетевая модель подвергается анализу и оптимизации по одному из ее параметров. Анализ позволяет оценить целесообразность структуры модели, определить степень сложности выполнения каждой работы, загрузку исполнителей работ на всех этапах выполнения комплекса работ. Относительная сложность соблюдения сроков выполнения работ на некритических путях характеризуется коэффициентом напряженности работКн(i,j): 
(4.16) где 
— продолжительность максимального пути, проходящего через данную работу; 
—продолжительность отрезка этого пути, совпадающего с критическим путем; 
—продолжительность критического пути. Чем больше коэффициент напряженности, тем сложнее выполнить работы в установленные сроки. Используя понятие «резерва времени пути», Кн(i,j) можно определить следующим образом: 
. (4.17) При этом необходимо иметь в виду, что резерв времени R(Li) пути Li может быть распределен между отдельными работами, находящимися на указанном пути, только в пределах зависимых резервов времени этих работ. Величина коэффициента напряженности у разных работ в сети лежит в пределах 0Кн(i,j) Кн(i,j) равен единице. Величина коэффициента напряженности помогает при установлении плановых сроков выполнения работ оценить, насколько свободно можно располагать имеющимися резервами времени. Этот коэффициент дает исполнителям работ представление о степени срочности работ и позволяет определить очередность их выполнения, если они не определяются технологическими связями работ. Для анализа сетевой модели используется коэффициент свободы Кс(i,j), который показывает степень свободы или независимости циклов работ, имеющих свободный резерв времени, а также показывает, во сколько раз можно увеличить длительность работы t(i, j), не влияя на сроки свершения всех событий и остальных работ сети: 
(4.18) При этом Кс(i,j) > 1 всегда. Если Кс(i,j) < 1, то это указывает на отсутствие независимого резервного времени у работы (i,j). Оптимизация сетевых моделей по одному из ее параметров может быть осуществлена графическим или аналитическим методом. Решая задачу оптимизации сетевой модели, обычно рассчитывают минимальную продолжительность выполнения комплекса работ при ограничениях на используемые ресурсы. Оптимизация сетевой модели, осуществляемая аналитическим методом, заключается в том, что в ее основу положена та закономерность, при которой время выполнения любой работы (t) прямо пропорционально ее объему (Q) и обратно пропорционально числу исполнителей (m), занятых на данной работе: 
(4.19) Время, необходимое для выполнения всего комплекса работ 
определяется как сумма длительностей составляющих работ: 
(4.20) Однако рассчитанное таким образом общее время не будет минимальным, даже если количество исполнителей соответствует трудоемкости этапов. Минимальное время для комплекса последовательно выполняемых работ и других разновидностей фрагментов сетевых моделей можно найти методом условно-эквивалентной трудоемкости. Под условно-эквивалентной трудоемкостью понимают такую величину затрат труда, при которой численность исполнителей эквивалентной специальности распределяется между составляющими работами, обеспечивает наименьшее время их исполнения. Условно-эквивалентная трудоемкость определяется по формуле: 
(4.21) где 
,
— трудоемкости предшествующей и последующей работ. Минимальное время выполнения работ будет обеспечено при следующем распределении работающих по этапам: 
(4.22) где m0 — общее количество работающих на определенных этапах.
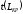
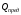
Параметры работ
Отдельная работа может начаться в ранние, поздние или другие промежуточные сроки.
Ранний срок tРН (i, j) начала работы(i, j) – это наиболее ранний (минимальный) из возможных моментов начала данной работы. Он, очевидно, совпадает с ранним сроком наступления ее начального события, то есть:
tРН (i, j)= tР (i) (4)
Тогда ранний срок tРО (i, j) окончания работы (i, j) определяется по формуле:
tРО (i, j)= tР (i)+ t (i, j) (5)
Поздний срок tПО (i, j) окончания работы (i, j) – наиболее поздний момент времени окончания этой работы, после которого остается столько времени, сколько его необходимо для выполнения всех последующих работ. И так как ни одна работа не может окончиться позже допустимого позднего срока своего конечного события j, поздний срок окончания работ (i, j) определяется соотношением:
tПО (i, j)= tП (j) (6)
а поздний срок tПН (i, j) начала этой работы – соотношением:
tПН (i, j)= tП (j)- t (i, j) (7)
Из формул (4) – (7) видно, что моменты начала и окончания работы тесно связаны с соседними событиями.
Резерв времени пути R(L) определяют как разность между длиной критического и рассматриваемого пути:
R(L)= tКР – t(L) (8)
Он показывает, насколько в сумме могут быть увеличены продолжительности всех работ, принадлежащих этому пути. Если затянуть выполнение работ, лежащих на этом пути, на время, большее, чем R(L), то критический путь переместится на путь L. Отсюда можно сделать вывод: любая из работ пути L на его участке, не совпадающем с критическим путем, обладаем резервом времени.
Среди резервов времени работ выделяют полный и свободный резервы времени.
Полный резерв времени RП (i, j) работы (i, j) – это максимально допустимое время, на которое можно увеличить продолжительность работы (i, j) или отложить начало ее выполнения так, что это не вызовет задержки выполнения всего комплекса работ. Полный резерв времени работы вычисляется по формуле:
RП (i, j) = tП (j)- tР (i)- t (i, j)= tПО (i, j)- tРО (i, j) (9)
Этим резервом можно располагать при выполнении данной работы, если ее начальное событие свершится в самый ранний срок и можно допустить свершение конечного события в его самый поздний срок.
Полный резерв времени работы равен резерву максимального из путей, проходящих через данную работу. При использовании полного резерва времени только для одной работы резервы времени остальных работ, лежащих на максимальном пути, проходящем через нее, будут полностью исчерпаны. Этот путь становится критическим. Резервы времени остальных путей, проходящих через эту работу, сократятся на величину использованного резерва.
Если полный резерв времени некоторой работы равен нулю, то задержка ее выполнения вызовет такую же по времени задержку выполнения всего комплекса работ.
Свободный резерв времени RС (i, j) работы (i, j) – максимальный запас времени, на который ее можно отложить (если она была запланирована в ранний срок) или увеличить ее продолжительность (если эта работа началась в ранний срок), не изменив при этом раннего срока ее конечного события.
Этим резервом можно располагать при выполнении данной работы в предположении, что ее начальное и конечное события свершаются в свои ранние сроки.
Свободный резерв времени (i, j) находится по формуле:
RС (i, j) = tР (j)- tР (i)- t (i, j) (10)
Свободный резерв времени работы является частью полного резерва:
RП (i, j) = RС (i, j)+ tП (j)- tР (j) (11)
Если на критическом пути лежит событие j, то RП (i, j) = RС (i, j).
Если использовать свободный резерв времени работы, то длина любого пути, проходящего через эту работу, сокращается на величину свободного резерва. На таких путях сохраняются свободные резервы всех последующих работ.
Свободным резервом времени пользуются для предотвращения случайностей, которые могут возникнуть в ходе выполнения работ. Если планировать выполнение работ по ранним срокам их начала и окончания, то всегда будет возможность при необходимости перейти на поздние сроки начала и окончания работ.
Работы, лежащие на критическом пути, так же как и критические события, резервов времени не имеют.
Вычислить для сетевого графика (рис.7) ранние и поздние сроки начала и окончания работ, их полные и свободные резервы времени. Найти все полные пути, вычислить их длину и резервы времени. Построить сетевой график в масштабе времени.
Чтобы найти указанные параметры работ, используем формулы (1) – (10), также результаты решения предыдущего примера, оформленные в виде сетевого графика (рис.8).
Результаты расчетов сведены в (табл. 2).
Графа 3 (табл. 2) заполняется с помощью сетевого графика (рис.8). Последовательно выписываются числа, стоящие в левых секторах кружков. Графу 4 (табл. 2) заполняют, складывая числа граф 2 и 3. Затем заполняется графа 6, выбирая последовательно числа из правых секторов кружков сетевого графика. Графа 7 равна разности граф 6 и 4. Графа 8 заполняется на основе формулы: RС (i, j) = tР (j)- tРО (i, j). Здесь числа tР (j) берутся из левых кружков графика 8, а tРО (i, j) – из графы 4. Для работы а1=(1,2). Она оканчивается в секторе кружка, моделирующего событие 2, поэтому tР (2) =15. Из графы 4 имеется tРО (1,2)=15. Значит RС (1,2) = 15-15=0. Для работы а7=(6,7) имеется tР (7)=45; tРО (6,7)=32. Поэтому RС (6,7) = 45-32=13 и т.д. Выявляют всевозможные полные пути для выполнения работ комплекса, находят их длину, резервы времени.
Таблица 2 – Результаты расчетов сетевого графика
Продолжительность t (i, j)