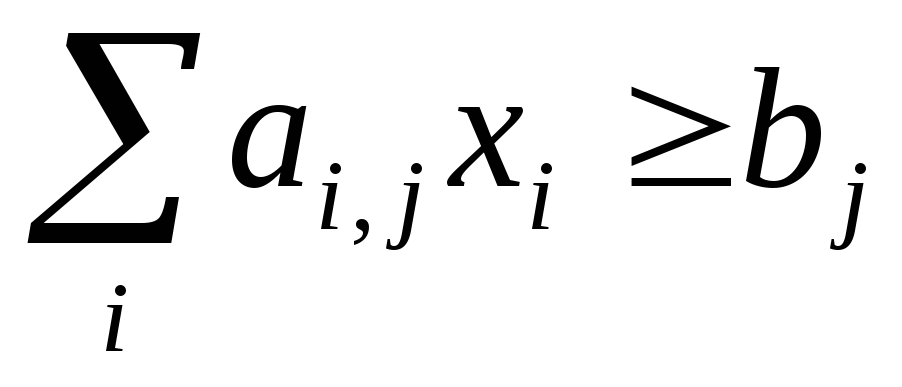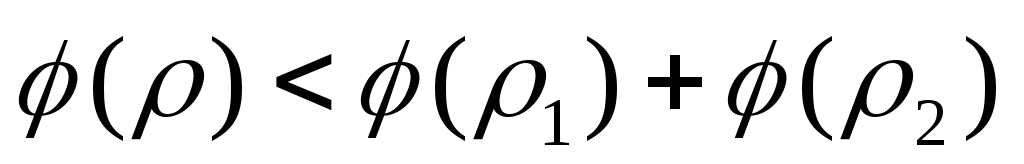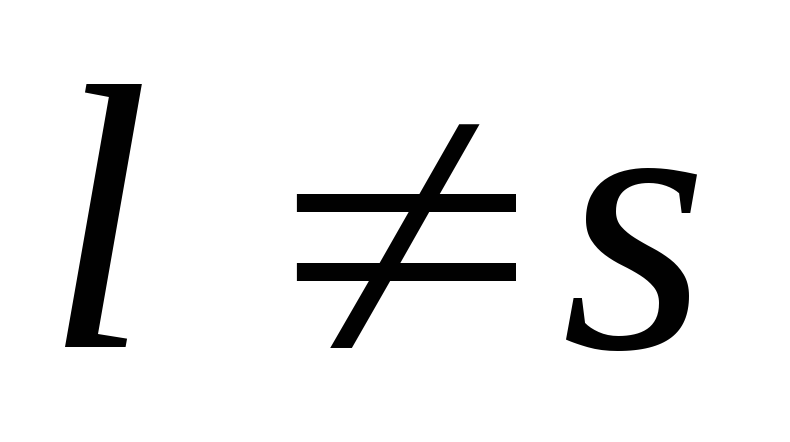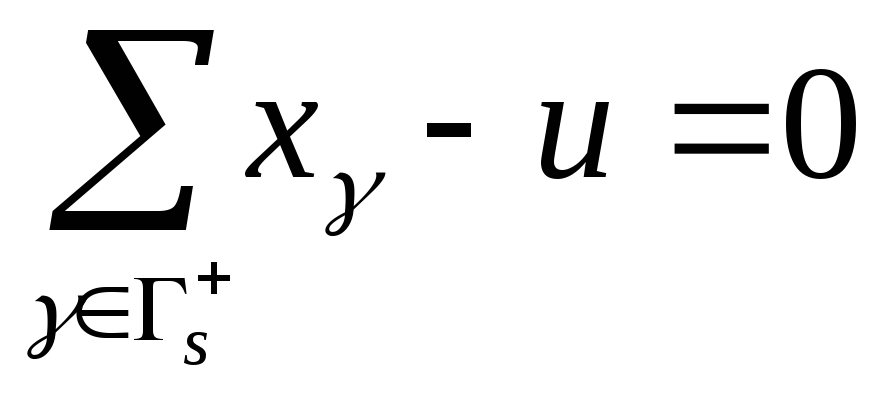4. Модели распределения транспортных потоков
Модели распределения транспортных потоков относятся к классу моделей, используемых для решения задач по оптимизации перевозок. В них, как правило, разыскивается оптимальный план перевозок между некоторой совокупностью производителей 

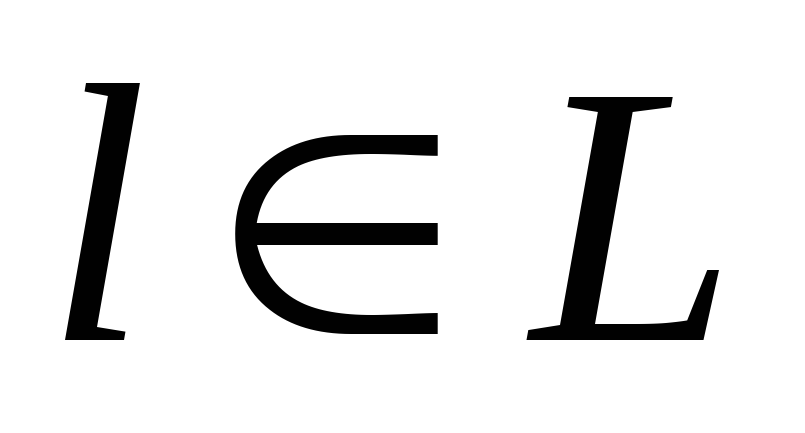



Существуют две основные формулировки этой задачи: в матричной и сетевой формах. При постановке в матричной форме задача распределения транспортных потоков сводится к транспортной задаче линейного программирования. При сетевой постановке задачи ее условия определяются на ориентированном мультиграфе с множествами узлов 

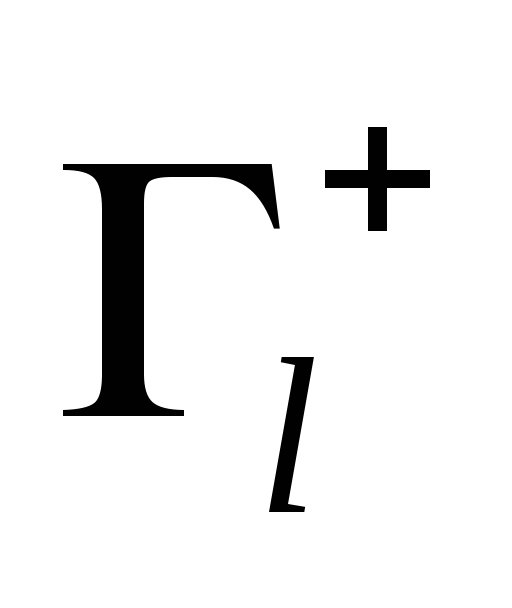



Через 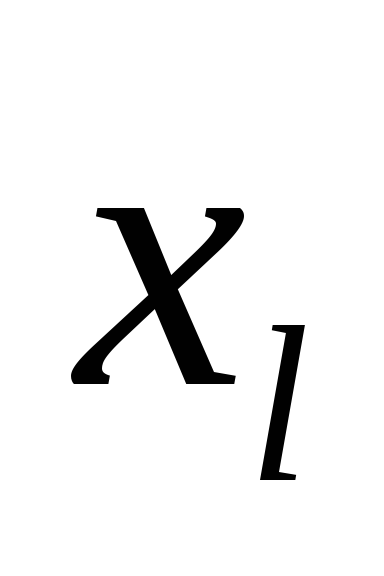


, (4.1.)
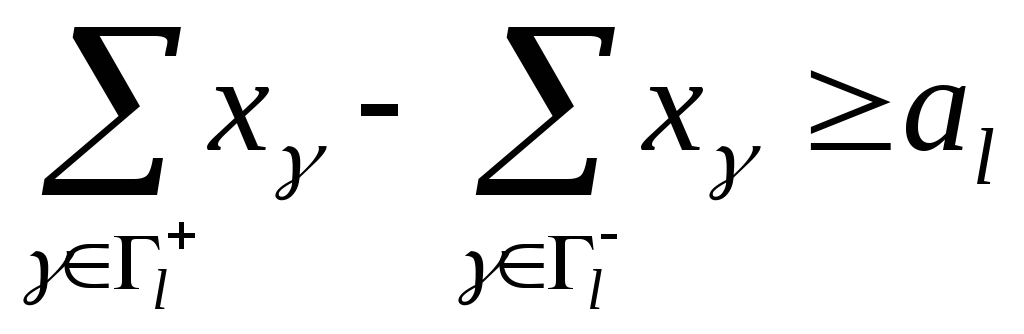


Для разрешимости задачи необходимо
. (4.3.)
Говорят, что величиной 
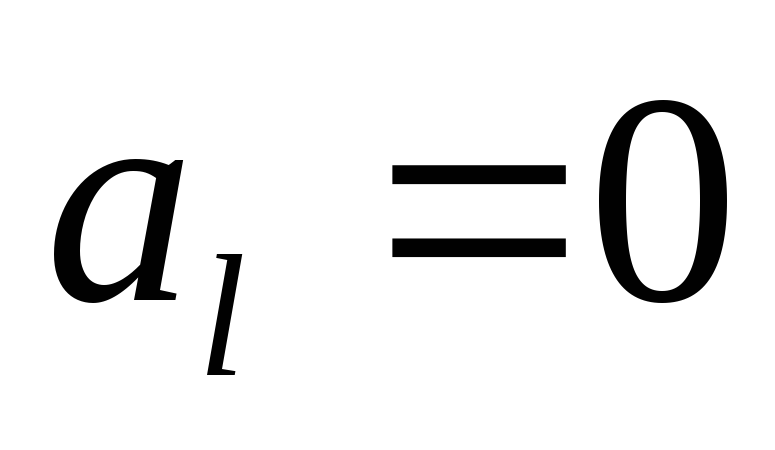
В случаях, когда неравенство (4.3.) выполняется строго, модель называется открытой, при выполнении же (4.3.) как равенства – закрытой (замкнутой). Присоединяя к открытой задаче сток с мощностью 
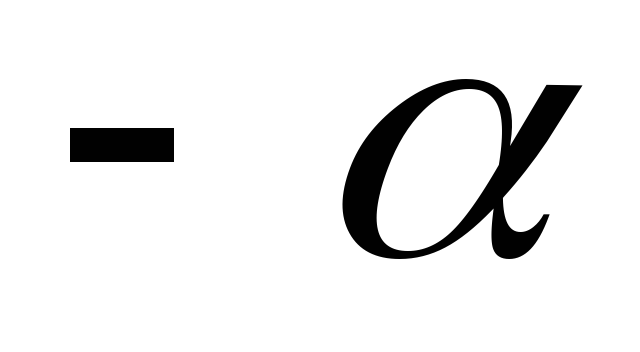

Иногда – при отождествлении величины 

Если сеть моделирует реальную структуру перевозок, то транспортные затраты должны рассчитываться в соответствии с тарифами. Обычно тариф представляет функцию 


. (4.4.)
В силу (4.4.) нельзя определить на дугах сети никакой системы коэффициентов транспортных затрат с тем, чтобы сумма их на любой последовательности дуг соответствовала тарифу. Поэтому модели распределения транспортных потоков обычно решается в два этапа.
На первом в реальной конфигурации сети определяют маршрут минимальной длины между всеми возможными парами поставщик – потребитель и по полученному набору дальностей – тарифные стоимости перевозок.
Затем на втором этапе ставится транспортная задача в матричной форме.
В сетевой задаче обычно существует много различных маршрутов, связывающих пару узлов сети. Поэтому она допускает ограничения на пропускные способности дуг
(4.5.)
Отмечая на сети два узла , можно дополнить условия (4.2.), (4.5.) равенствами

и заменить критерий (4.1.) требованием .
Эта модель известна как задача о максимальной пропускной способности сети.
Задача раскроя заключается в выборе такого размещения заготовок в кусках материала, которое дает заготовки, как правило, в требуемой комплектности при минимальном расходе материала. В соответствии с особенностями в технологии и организации раскроя различаются математические модели рационального раскроя для массового и индивидуального производства:
- для прямых (отрезки, прямоугольники, параллелепипеды) и фигурных заготовок;
- для случая кусков материала постоянных размеров и форм и с разбросом формы.
В зависимости от отрасли производства и используемого оборудования учитываются ограничения на допустимые виды раскроев. С задачами раскроя совпадает постановка некоторых задач размещения грузов в сушильных печах, в вагонах, на палубах и трюмов судов. В массовом производстве при поступлении одинаковых кусков материал, если можно перечислить все (




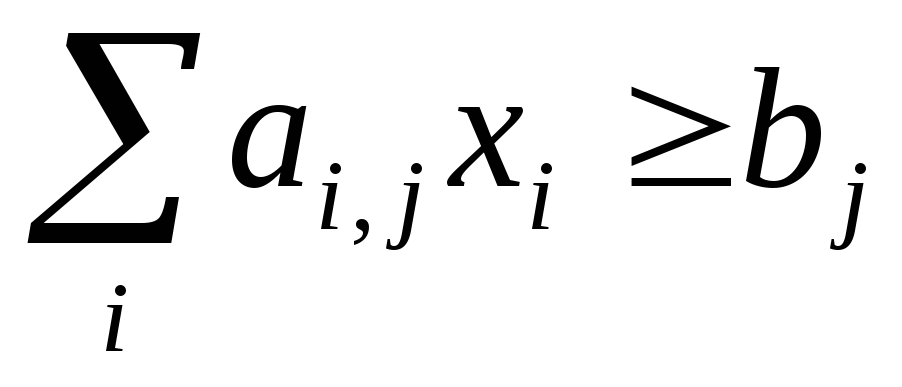




4. Модели распределения транспортных потоков
Модели распределения транспортных потоков относятся к классу моделей, используемых для решения задач по оптимизации перевозок. В них, как правило, разыскивается оптимальный план перевозок между некоторой совокупностью производителей 

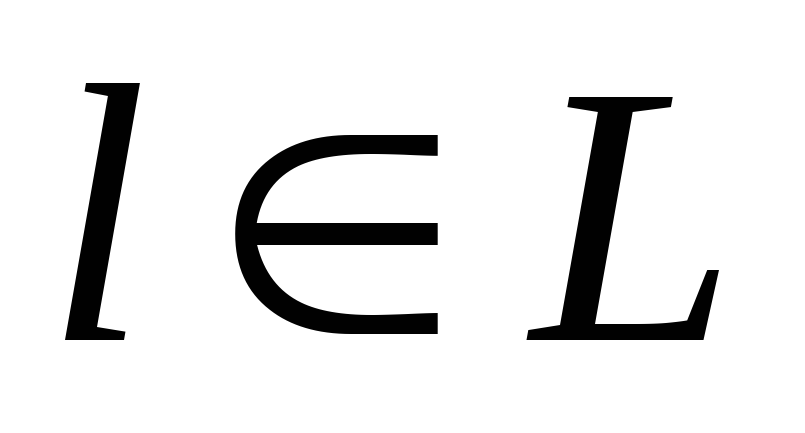



Существуют две основные формулировки этой задачи: в матричной и сетевой формах. При постановке в матричной форме задача распределения транспортных потоков сводится к транспортной задаче линейного программирования. При сетевой постановке задачи ее условия определяются на ориентированном мультиграфе с множествами узлов 

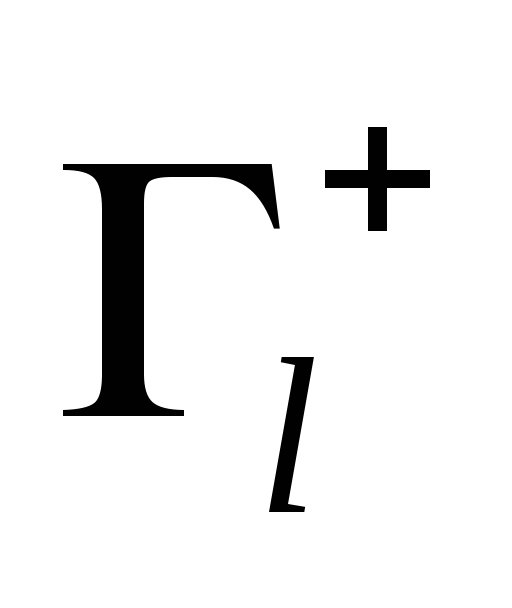



Через 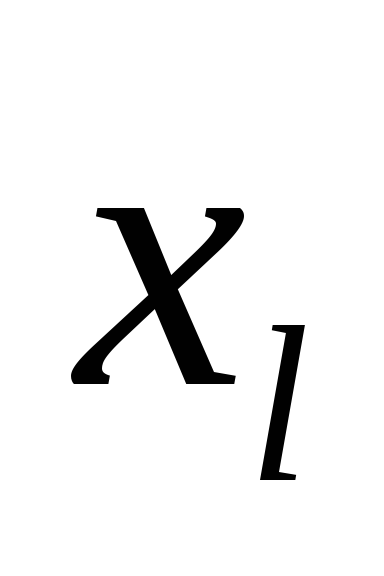


, (4.1.)
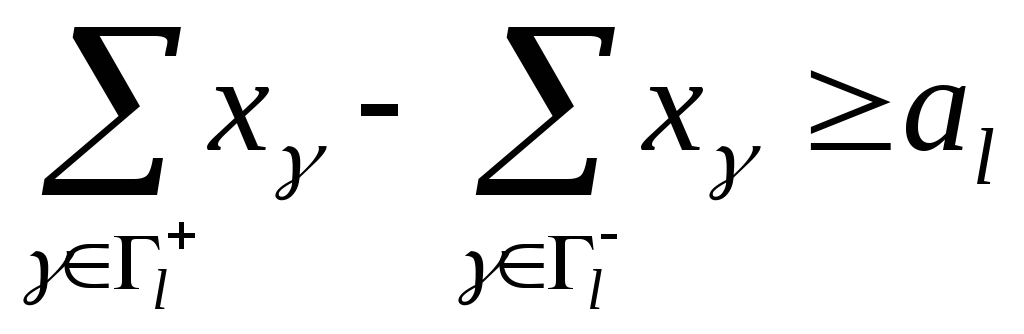


Для разрешимости задачи необходимо
. (4.3.)
Говорят, что величиной 
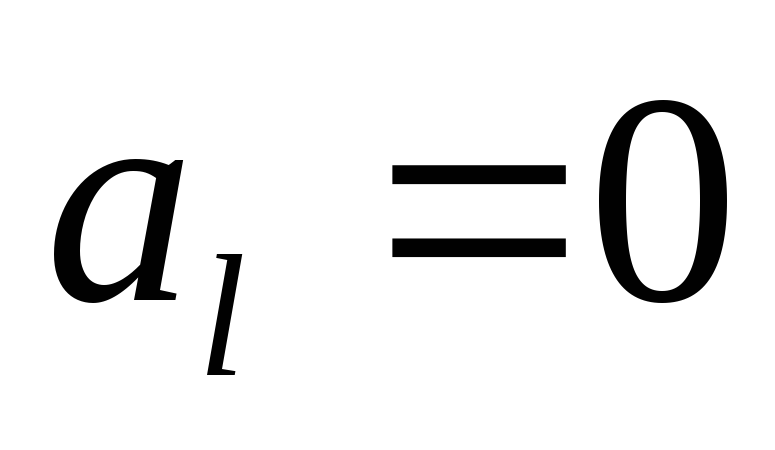
В случаях, когда неравенство (4.3.) выполняется строго, модель называется открытой, при выполнении же (4.3.) как равенства – закрытой (замкнутой). Присоединяя к открытой задаче сток с мощностью 
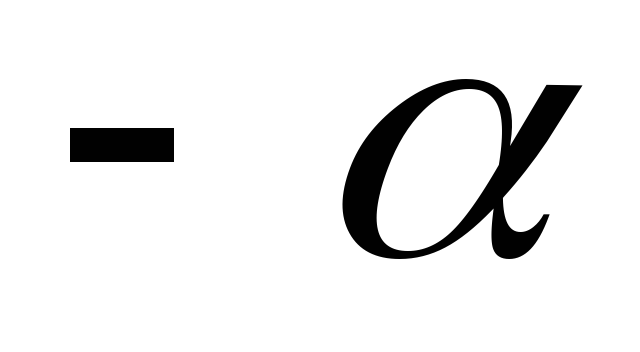

Иногда – при отождествлении величины 

Если сеть моделирует реальную структуру перевозок, то транспортные затраты должны рассчитываться в соответствии с тарифами. Обычно тариф представляет функцию 


. (4.4.)
В силу (4.4.) нельзя определить на дугах сети никакой системы коэффициентов транспортных затрат с тем, чтобы сумма их на любой последовательности дуг соответствовала тарифу. Поэтому модели распределения транспортных потоков обычно решается в два этапа.
На первом в реальной конфигурации сети определяют маршрут минимальной длины между всеми возможными парами поставщик – потребитель и по полученному набору дальностей – тарифные стоимости перевозок.
Затем на втором этапе ставится транспортная задача в матричной форме.
В сетевой задаче обычно существует много различных маршрутов, связывающих пару узлов сети. Поэтому она допускает ограничения на пропускные способности дуг
(4.5.)
Отмечая на сети два узла , можно дополнить условия (4.2.), (4.5.) равенствами

и заменить критерий (4.1.) требованием .
Эта модель известна как задача о максимальной пропускной способности сети.
Задача раскроя заключается в выборе такого размещения заготовок в кусках материала, которое дает заготовки, как правило, в требуемой комплектности при минимальном расходе материала. В соответствии с особенностями в технологии и организации раскроя различаются математические модели рационального раскроя для массового и индивидуального производства:
- для прямых (отрезки, прямоугольники, параллелепипеды) и фигурных заготовок;
- для случая кусков материала постоянных размеров и форм и с разбросом формы.
В зависимости от отрасли производства и используемого оборудования учитываются ограничения на допустимые виды раскроев. С задачами раскроя совпадает постановка некоторых задач размещения грузов в сушильных печах, в вагонах, на палубах и трюмов судов. В массовом производстве при поступлении одинаковых кусков материал, если можно перечислить все (