Модель транспортной сети
Модель транспортной (геометрической) сети предназначена, в первую очередь, для описания в виде связанного графа схемы транспортных коммуникаций (автомобильных и железных дорог, авиалиний и водных маршрутов) с целью последующего сетевого анализа.
Транспортная сеть содержит два основных типа объектов (узлы и дуги), а также один дополнительный – маршруты.
1. Узлы являются обычными точечными объектами, характеризуемыми координатами на плоскости (х,у). Узлы могут дополнительно характеризоваться такими параметрами, как запреты на выполнение некоторых поворотов и время их выполнения.
2. Дуги являются линейными объектами – ломаными, соединяющими пару узлов транспортной сети и проходящими через последовательность промежуточных точек. Каждая дуга характеризуется длиной или временем движения по ней, разрешенными направлениями движения, классом дороги или пропускной способностью и др.
3. Дополнительно на транспортной сети могут быть определены объекты еще одного типа – маршруты движения транспорта (рис. 13). Каждый маршрут определяется как замкнутая упорядоченная последовательность узлов и дуг, а также различными числовыми характеристиками (например, расчетное время прохождения транспорта через остановки).
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Это важно знать:
Методы и средства гигиенического обучения и воспитания населения Гигиеническое воспитание (санитарное просвещение) — совокупность образовательных.
Юридические факты: понятие, признаки, функции, виды Основанием возникновения, изменения и прекращения правоотношений являются юридические факты — указания, которые содержатся.
Медиана для интервального ряда Квантили Квантили — величины, разделяющие совокупность на определенной количество равных по численности элементов частей.
Научное познание Научное познание — это вид и уровень познания, направленный на производство истинных знаний о действительности, открытие.
В каких случаях назначается ответственный руководитель работ, выполняемых по наряду? Ответственный руководитель работ назначается, как правило, при работах в электроустановках напряжением выше 1000 В.
Анализ транспортной сети — Transport network analysis
Транспортная сеть , или транспортная сеть является сетью или график , в географическом пространстве, описывающая инфраструктуру , которая допускает и сдерживает движение или течь. Примеры включают, но не ограничиваются ими, дорожные сети , железные дороги , воздушные маршруты , трубопроводы , акведуки и линии электропередач . Цифровое представление этих сетей и методы их анализа являются основной частью пространственного анализа , географических информационных систем , коммунальных служб и транспортного машиностроения . Сетевой анализ — это приложение теорий и алгоритмов теории графов и форма анализа близости .
История
Применимость теории графов к географическим явлениям была признана рано. Фактически, многие из ранних проблем и теорий, предпринятых теоретиками графов, были вдохновлены географическими ситуациями, такими как проблема семи мостов Кенигсберга , которая была одной из первоначальных основ теории графов, когда она была решена Леонардом Эйлером в 1736 году.
В 1970-х годах эта связь была восстановлена первыми разработчиками географических информационных систем , которые использовали ее в топологических структурах данных полигонов (что здесь не имеет значения) и анализе транспортных сетей. Ранние работы, такие как Tinkler (1977), были сосредоточены в основном на простых схематических сетях, вероятно, из-за отсутствия значительных объемов линейных данных и вычислительной сложности многих алгоритмов. Полная реализация алгоритмов сетевого анализа в программном обеспечении ГИС не появлялась до 1990-х годов, но довольно продвинутые инструменты, как правило, доступны сегодня.
Сетевые данные
Сетевой анализ требует подробных данных, представляющих элементы сети и ее свойства. Ядром набора сетевых данных является векторный слой из полилиний, представляющих пути движения, точные географические маршруты или схематические изображения, известные как края . Кроме того, необходима информация о топологии сети , представляющей соединения между линиями, что позволяет моделировать транспорт от одной линии к другой. Обычно эти точки подключения или узлы включаются в качестве дополнительного набора данных.
И ребрам, и узлам приписываются свойства, связанные с движением или потоком:
- Пропускная способность , измерения любых ограничений допустимого объема потока, например количества полос на дороге, пропускной способности канала связи или диаметра трубы.
- Импеданс , измерения любого сопротивления потоку или скорости потока, например, ограничение скорости или запрещенное направление поворота на перекрестке улиц.
- Стоимость, накапливаемая в результате индивидуального путешествия по краю или через узел, обычно затраченное время, в соответствии с принципом трения расстояния . Например, узлу уличной сети может потребоваться разное количество времени, чтобы сделать конкретный поворот налево или направо. Такие затраты могут меняться с течением времени, например, время в пути по городской улице в зависимости от суточных циклов интенсивности движения.
- Объем потока , измерения фактического движения. Это могут быть конкретные измерения с временной кодировкой, собранные с помощью сенсорных сетей, таких как счетчики трафика , или общие тенденции за период времени, такие как среднегодовой дневной трафик (AADT).
Методы анализа
Для решения проблем и задач, связанных с сетевым потоком, был разработан широкий спектр методов, алгоритмов и приемов. Некоторые из них являются общими для всех типов транспортных сетей, а другие специфичны для конкретных доменов приложений. Многие из этих алгоритмов реализованы в коммерческом программном обеспечении ГИС с открытым исходным кодом, таком как GRASS GIS и расширение Network Analyst для Esri ArcGIS .
Оптимальная маршрутизация
Одна из простейших и наиболее распространенных задач в сети — найти оптимальный маршрут, соединяющий две точки в сети, при этом оптимальный определяется как минимизация некоторой формы затрат, таких как расстояние, затраты энергии или время. Типичный пример — поиск направлений в уличной сети, функция практически любого веб-приложения для картографии улиц, такого как Google Maps . Самым популярным методом решения этой задачи, реализованным в большинстве программ ГИС и картографии, является алгоритм Дейкстры .
В дополнение к базовой двухточечной маршрутизации также распространены проблемы составной маршрутизации . Задача коммивояжера требует оптимального (наименьшее расстояние / стоимость) заказа и маршрута для достижения ряда пунктов назначения; это NP-сложная проблема, но ее несколько легче решить в сетевом пространстве, чем в неограниченном, из-за меньшего набора решений. Проблема маршрутизации транспортных средств является ее обобщением, позволяя использовать несколько одновременных маршрутов для достижения пункта назначения. Осмотр маршрута или проблема «Китайский Почтальон» запрашивает оптимальной (наименьшее расстояние / стоимость) путь , который проходит через каждое ребро; обычное приложение — это маршрутизация мусоровозов. Оказалось, что эту задачу гораздо проще решить с помощью алгоритмов с полиномиальным временем .
Анализ местоположения
Этот класс задач направлен на поиск оптимального местоположения для одного или нескольких объектов в сети, при этом оптимальное определяется как минимизация совокупной или средней стоимости проезда к (или от) другому набору точек в сети. Распространенным примером является определение местоположения склада для минимизации затрат на доставку в набор розничных торговых точек или расположение розничной торговой точки для минимизации времени в пути от места жительства его потенциальных клиентов. В неограниченном (декартово координатном) пространстве это NP-сложная задача, требующая эвристических решений, таких как алгоритм Ллойда , но в сетевом пространстве ее можно решить детерминированно.
Конкретные приложения часто добавляют дополнительные ограничения к проблеме, такие как расположение уже существующих или конкурирующих объектов, мощность объекта или максимальная стоимость.
Зоны обслуживания
Зона обслуживания сети аналогична буферу в неограниченном пространстве, изображению области, которая может быть достигнута из точки (обычно объекта обслуживания) на меньшем расстоянии, чем указанное расстояние или другие накопленные затраты. Например, предпочтительной зоной обслуживания пожарного депо будет набор сегментов улицы, который он может достичь за небольшой промежуток времени. Когда имеется несколько предприятий, каждое ребро будет назначено ближайшему предприятию, что даст результат, аналогичный диаграмме Вороного .
Анализ неисправностей
Распространенным применением в коммунальных сетях общего пользования является определение возможных местоположений неисправностей или разрывов в сети (которые часто скрыты под землей или их трудно наблюдать напрямую) на основе отчетов, которые можно легко найти, таких как жалобы потребителей.
Транспортное машиностроение
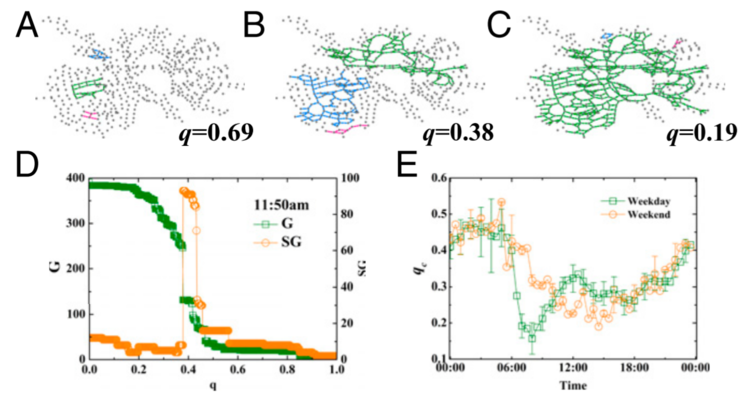
Движение широко изучено с использованием методов статистической физики. Недавно реальная транспортная сеть Пекина была изучена с использованием сетевого подхода и теории перколяции. Исследование показало, что можно охарактеризовать качество глобального трафика в городе в любое время дня, используя порог перколяции, см. Рис. 1. В недавних статьях теория перколяции применялась для изучения загруженности дорог в городе. Качество глобального трафика в городе в данный момент времени определяется одним параметром — критическим порогом перколяции. Критический порог представляет собой скорость, ниже которой можно двигаться в значительной части городской сети. Этот метод позволяет выявить повторяющиеся узкие места трафика. Критические показатели, характеризующие распределение хорошего трафика по размеру кластера, аналогичны показателям теории перколяции. Также обнаружено, что в часы пик транспортная сеть может иметь несколько метастабильных состояний разных размеров сети и чередоваться между этими состояниями.
Эмпирическое исследование распределения размеров пробок было недавно проведено Zhang et al. Они нашли примерный универсальный степенной закон для распределения размеров затора.
Серок и др. Разработали метод определения функциональных кластеров пространственно-временных улиц, которые представляют свободный транспортный поток в городе. G. Li et al. разработал метод построения оптимальной двухуровневой транспортной сети в городе.
Рис. 1: Распространение транспортных сетей в типичный день в Пекине. A Показывает высокоскоростные кластеры. В B можно увидеть кластеры на критическом пороге, где гигантский компонент разрушается. C Показывает случай низкой скорости, когда можно добраться до всего города. В D можно увидеть перколяционное поведение самого большого (зеленый) и второго по величине (оранжевый) компонентов в зависимости от относительной скорости. E Показывает критический порог q в течение дня для рабочих и выходных дней. Высокое q означает хороший глобальный трафик, а низкое q — плохой трафик — в час пик. c c c
Модели потоков трафика
Речные модели транспортных потоков в городских районах больших городов в часы пик и не в часы пик были изучены Yohei Shida et al.