1. Сетевая модель и ее основные элементы.
Сетевая модель представляет собой план выполнения некоторого комплекса взаимосвязанных работ (операций), заданного в специфической форме сети, графическое изображение которой называется сетевым графиком. Отличительной особенностью сетевой модели является четкое определение всех временных взаимосвязей предстоящих работ.
Главными элементами сетевой модели являются событиями и работы
Термин работа используется в СПУ в широком смысле.Во-первых, это действительная работа — протяженный во временипроцесс, требующий затрат ресурсов (например, сборка изделия, испытание прибора и т.п.). Каждая действительная работа, должна быть конкретной, четко описанной и иметь ответственного исполнителя.
Во-вторых, это ожидание — протяженный во времени процесс,не требующий затрат труда (например, процесс сушки после окраски, старения металла, твердения бетона и т.п.).
В-третьих, это зависимость, или фиктивная работа — логическая связь между двумя или несколькими работами (события), не требующими затрат труда, материальных ресурсов или времени. Она указывает, что возможность одной работы непосредственно зависит от результатов другой. Естественно, что продолжительность фиктивной работы принимается равной нулю.
Событие — это момент завершения какого-либо процесса, отражающий отдельный этап выполнения проекта. Событие может являться частным результатом отдельной работы или суммарным результатом нескольких работ. Событие может свершиться только тогда, когда закончатся все работы, ему предшествующие. Последующие работы могут начаться только тогда, когда событие свершится. Отсюда двойственный характер события: для всех непосредственно предшествующих ему работ оно является конечным, а для всех непосредственно следующих за ним — начальным. При этом предполагается, что событие не имеет продолжительности и свершается как бы мгновенно. Поэтому каждое событие, включаемое в сетевую модель, должно быть полно, точно и всесторонне определено, его формулировка должна включать в себя результат всех непосредственно предшествующих ему работ.
Среди событий сетевой модели выделяют исходное и завершающее события. Исходное событие не имеет предшествующих работ и событий, относящихся к представленному в модели комплексу работ. Завершающее событие не имеет последующих работ и событий.
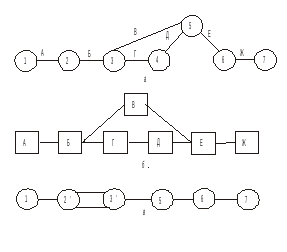
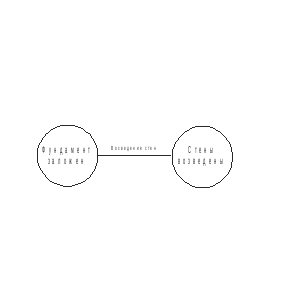
События на сетевом графике (или, как еще говорят, на графе)изображаются кружками (вершинами графа), а работы — стрелками(ориентированными дугами), показывающими связь между работами. Пример фрагмента сетевого графика представлен на рис 1:
На рис. 2, а приведен сетевой график задачи моделирования и построения оптимального плана некоторого экономического объекта. Чтобы решить эту задачу, необходимо провести следующие работы: А – сформулировать проблему исследования; В5 — математическую модель изучаемого объекта; В — собрать информацию; Г — выбрать метод решения задачи; Д — построить и отладить программу для ЭВМ; Е — рассчитать оптимальный план; Ж — передать результаты расчета заказчику. Цифрами на графике обозначены номера событий, к которым приводит выполнение соответствующих работ.
Из графика, например, следует, что работы В и Г можно начать выполнять независимо одна от другой только после свершения события 3, т.е. когда выполнены работы А и Б; работу Д — после свершения события 4, когда выполнены работы А, Б и Г; а работу Е можно выполнить только после наступления события 5, т.е. при выполнении всех предшествующих ему работ А, Б, В, Г и Д.
В сетевой модели, представленной на рис. 2 а, нет числовых оценок. Такая сеть называется структурной. Однако на практике чаще всего используются сети, в которых заданы оценки продолжительности работ (указываемые в часах, неделях, декадах, месяцах и т.д. над соответствующими стрелками), а также оценки других параметров, например трудоемкости, стоимости и т.п. Именно такие сети мы будем рассматривать в дальнейшем.
Но прежде сделаем следующее замечание. В рассмотренных примерах сетевые графики состояли из работ и событий. Однако может быть и иной принцип построения сетей — без событий. В такой сети вершины графа (например, изображенные прямоугольниками) означают определенные работы, а стрелки — зависимости между этими работами, определяющие порядок их выполнения. В качестве примера сетевой график «события — работы» задачи моделирования и построения оптимального плана некоторого экономического объекта, приведенный на рис. 2 а, представлен в виде сети «работы — связи» на рис. 2 б. А сетевой график «события — работы» той же задачи, но с неудачно составленным перечнем работ, представлен на рис. 2 в (см. правило 3 в разд. 3).
Следует отметить, что сетевой график «работы — связи» в отличие от графика «события — работы» обладает известными преимуществами: не содержит фиктивных работ, имеет более простую технику построения и перестройки, включает только хорошо знакомое исполнителям понятие работы без менее привычного понятия события. Вместе с тем сети без событий оказываются значительно более громоздкими, так как событий обычно значительно меньше, чем работ (показатель сложности сети, равный отношению числа работ к числу событий, как правило, существенно больше единицы). Поэтому эти сети менее эффективны с точки зрения управления комплексом. Этим и объясняется тот факт, что (при отсутствии в целом принципиальных различий между двумя формами представления сети) в настоящее время наибольшее распространение получили сетевые графики «события — работы».
Сетевая модель
Сетевая модель данных позволяет отображать разнообразные взаимосвязи элементов данных в виде произвольного графа (не обязательно дерева), обобщая тем самым иерархическую модель данных. При этом в сетевой модели ребра графа являются ориентированными (т.е. линиями со стрелкой, идущими от предка к потомку). Стандарт сетевой модели впервые был определен в 1975 году организацией CODASYL (Conference of Data System Languages), которая определила базовые понятия модели и формальный язык описания.
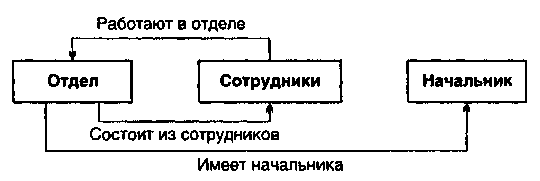
Для описания схемы сетевой БД используются термины «запись» и «связь». «Связь» (направленная стрелка) определяется для «записей»: предка и потомка. Разумеется, записи и связи так же, как и в иерархической модели, могут иметь много экземпляров.
Сетевая БД состоит из набора записей и набора соответствующих связей. На формирование связи особых ограничений не накладывается. Если в иерархических структурах запись-потомок могла иметь только одну запись-предка, то в сетевой модели данных запись-потомок может иметь произвольное число записей-предков.
Пример схемы простейшей сетевой БД показан ниже (типы связей здесь обозначены надписями на соединяющих типы записей линиях).
Физическое размещение данных в базах сетевого типа может быть организовано практически теми же методами, что и в иерархических базах данных.(
К числу важнейших операций манипулирования данными баз сетевого типа можно отнести следующие: поиск записи в БД; переход от предка к первому потомку; переход от потомка к предку; создание новой записи; удаление текущей записи; обновление текущей записи; включение записи в связь; исключение записи из связи; изменение связей и т. д.
Достоинством сетевой модели данных является возможность эффективной реализации по показателям затрат памяти и оперативности. В сравнении с иерархической моделью сетевая модель предоставляет большие возможности в смысле допустимости образования произвольных связей.
Недостатком сетевой модели данных является высокая сложность и жесткость схемы БД, построенной на ее основе, а также сложность для понимания и выполнения обработки информации в БД обычным пользователем. Кроме того, в сетевой модели данных ослаблен контроль целостности связей вследствие допустимости установления произвольных связей между записями.
Системы на основе сетевой модели не получили широкого распространения на практике.
Реляционная модель
Реляционная модель данных предложена сотрудником фирмы IBM Эдгаром Коддом в 1969—1970 гг. на основе математической теории отношений (отношение по-английски relation, отсюда и название модели).
Рассмотрим основные понятия теории отношений. Пусть имеется п множеств, называемых в реляционной модели доменами: Dl, D2. Dn (п > 1). n-арным отношением на этих множествах называют любую совокупность упорядоченных наборов вида (dlj , d2j, . , dnJ>), где dlj еcть элемент множества Dl, d2j еcть элемент множества D2, и так далее, dnj ecть элемент множества Dn. Например, если D1 есть совокупность фамилий, имен и отчеств студентов некоторой группы, D2 — совокупность учебных дисциплин, a D3 — совокупность оценок (например, или ), то 3-арное отношение (или отношение арности 3, или отношение ранга 3, или отношение степени 3) на множествах Dl, D2, D3 представляет собой результаты экзаменов в группе:
(Иванов Иван Иванович, Информатика, хорошо)
(Иванов Иван Иванович, Экономика, отлично)
(Петров Петр Петрович, Информатика, удовлетворительно)
(Петров Петр Петрович, Экономика, хорошо)
Очевидно, такое отношение не обязательно содержит все сочетания «студент — учебная дисциплина», т. е. может (и должно) отражать текущее состояние экзаменационной сессии.
Отношение наглядно изображается в виде таблицы (назовем ее «Экзамен»), в которой количество колонок равно арности (рангу, степени) отношения, их наименования (атрибуты отношения) соответствуют доменам отношения, а строки таблицы представляют собой элементы отношения: