Сетевая модель задачи и ее решение.
Изобразим моменты i=1,2. N+1 в виде вершин графа, а пары (i,j) в виде ориентированных дуг этого графа (основные понятиятеории графови терминология приведены в Приложении). Проставим на дугах (i,j) соответствующие стоимости арендыCijи будем считать их длинами этих дуг. Тогда произвольный планможно представить как путь из вершины1в вершинуN+1, а стоимость плана – длиной этого пути. Наоборот, каждый путь указанного вида является планом аренды. Оптимальным планом аренды будет кратчайший путь из1вN+1. Таким образом, задача об аренде оборудования является частным случаем известной задачи о нахождении кратчайшего пути (маршрута) [1,2,4].
Полученный граф (сеть) с заданными числами-стоимостями на дугах называется сетевой модельюзадачи об аренде оборудования, а нахождение оптимального плана (оптимальных планов) аренды как кратчайшего пути на этой сети – решением на сетевой модели.
Найдём путь методом потенциалов[2-3, 6] для бесконтурных сетей.
На 1-м этапе находим потенциалы— числаVi для каждой вершиныi, означающие кратчайшие расстояния от вершиныiдо конечной вершиныN+1. Потенциалы найдем, начиная с последней и далее по убыванию номеров вершин по формуле
; 
,
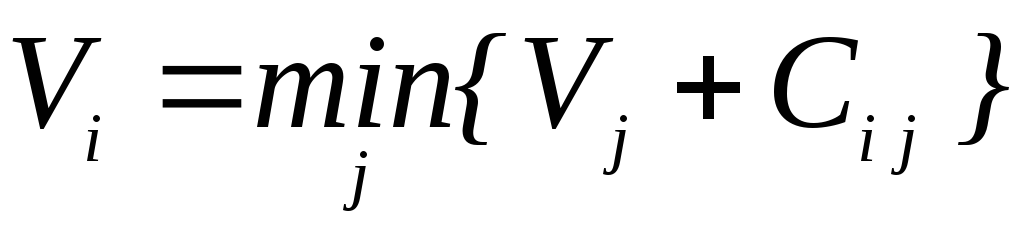
минимум берётся по всем дугам (i,j),выходящимизвершиныi .
На втором этапе, начиная с вершины i=1, находятся и выделяются дуги (i,j), на которых потенциал начала дуги
в точности равен сумме потенциала конца дуги
и стоимости дугиCij. Выделенные таким образом дуги дают кратчайший путь (пути), то есть оптимальные планы аренды. Потенциал
начальной вершины будет равен длине кратчайшего пути, то есть стоимости оптимального плана аренды.
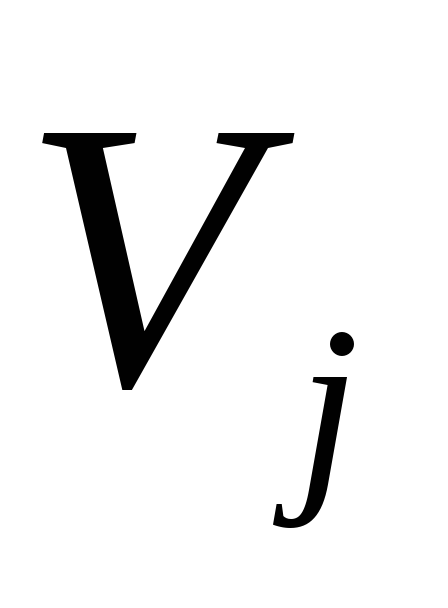
Пример 2. . Пусть при N=6 стоимости аренды Cij заданы в таблице:
j
Сетевое планирование
Основное назначение методологии сетевого планирования в управлении сократить до минимума продолжительность проекта. С помощью сетевых моделей руководитель может системно оценивать текущий и перспективный ход запланированных операций, за счет чего возможно управление процессом реализации проекта в целом. Календарно-сетевое планирование позволяет также рационально оперировать имеющимися в распоряжении ресурсами.
Основная цель сетевого планирования следует из его назначения: построить модель реализации проекта на основе формирования комплекса работ, задания их очередности, определить необходимые ресурсы и задачи, которые должны быть решены для завершения проекта. В итоге необходимо добиться сокращения до минимума продолжительности проекта.
Метод сетевого планирования позволяет координировать деятельность участников проекта, определить порядок, согласно которому должны выполняться запланированные работы, операции, действия. При этом основу составляет продолжительность каждой операции, действия, которые должны быть определены с учетом потребностей в материальных, трудовых и финансовых ресурсах.
Сетевое планирование – это метод управления, основанный на математическом аппарате теории графов и системного подхода, преследует задачи объективного построения плана операций на заданный период времени за счет алгоритмизации взаимосвязанных работ. Благодаря такому подходу достигается поставленная цель.
Применение методологии сетевого планирования в управлении предполагает формализацию структуры операций в информационно-табличном виде, на основе чего осуществляется структуризация операций по отрезкам времени и группировка параллельных операций для оптимального выполнения всего проекта в целом. На основе этого осуществляется построение таблицы операций, в которую сводятся все значимые данные по каждой операции в соответствии с формализованной структурой операций и группами параллельных операций. Результатом является построение сетевой диаграммы, которая подлежит корректировке в случае несоответствия запланированных действий общему сроку их выполнения, либо отдельным промежуткам времени внутри общей временной структуры проекта.
Задачи сетевого планирования:
- Определить перечень критических работ или операций (т.е. таких операций, которые имеют наибольшее влияние на общую продолжительность проекта);
- Построить сетевой план проекта таким образом, чтобы все запланированные работы и операции были произведены с соблюдением заданных сроков и минимальных затратах.
Единица такой сетевой модели – операция (работа или задача), которая означает какую-либо деятельность, в результате выполнения которой будут достигнуты определенные результаты.
Результатом сетевого планирования является графическое отображение последовательности операций, выполнение которых приведет к достижению конечной цели проекта. Основным способом отображения являются сетевые экономико-математические модели. Для управленческой деятельности наиболее подходят сетевые графики. С помощью сетевой модели формируется возможность системного представления всех операций и условия для управления процессом осуществления проекта. При необходимости метод сетевого планирования позволяет маневрировать ресурсами в рамках модели для достижения конечной цели.
Часто руководители склонны опираться лишь на личный опыт, который ограничен и субъективен. Такой ограниченный уровень компетентности редко помогает в динамичном окружении, а иногда может принести прямой вред.
Сетевое планирование позволяет исключить влияние субъективных факторов на управление проектом, способствуя сокращению сроков реализации проекта минимум на 15-20%, рационализации использования имеющихся ресурсов и оптимизации затрат. При этом отдельные операции рассматриваются как отдельные элементы целостной системы, а исполнители выступают звеньями данной системы.
Методы сетевого планирования
Применяя сетевые диаграммы (граф сети, PERT-диаграммы), следует учитывать следующие аспекты:
- сетевая диаграмма отражает полный комплекс работ и этапов проекта;
- на сетевом графике должны быть установлены зависимости между операциями;
- сетевые графики не являются блок-схемами;
- сетевые диаграммы содержат только операции и логические зависимости между ними (отсутствуют входы, процессы, выходы и т.д.);
- сетевые модели не допускают повторяющихся циклов, этапов, «петель» операций.
Сетевое планирование ориентировано на сокращение до минимума продолжительности проекта, для жтого могут применяться два метода:
«Максимальный по продолжительности полный путь в сети называется критическим; работы, лежащие на этом пути, также называются критическими. Именно длительность критического пути определяет наименьшую общую продолжительность работ по проекту в целом» [1]. Увеличение или сокращение времени выполнения операций критического пути ведет к росту и снижению продолжительности проекта соответственно. Метод критического пути предполагает расчет графиков работ, продолжительности каждой работы, чтобы определить критический путь проекта, а затем принять меры по его сокращению.
Метод оценки и пересмотра планов заключается в соблюдении графиков проектирования, производства, организации работ и других установленных сроков. Согласно этой методике, весь проект «разбивается» на ряд подзадач, и для каждой задачи оценивается время, необходимое для ее выполнения, каждой задаче также назначается приоритет выполнения. В зависимости от приоритета задачи и ее влияния на проект предпринимаются меры по оптимизации ее выполнения для снижения продолжительности проекта.
Таким образом, процесс сетевого планирования заключается в описании конкретного проекта или плана действий на заданный период в виде определенного комплекса мероприятий, задач, мер, процедур или работ.
При этом соблюдается объектная взаимосвязь между всеми процедурами и операциями, которые включены в структуру проекта или плана действий на заданный период. Развитие методик управления проектами в начале XXI века привело к тому, что в случае несоответствия реальной технологии выполнения работ сетевое планирование превращается в «формальную галочку», как следствие, дискредитируется сама идея использования технологий календарно-сетевого планирования.
Методика построения сетевых моделей
Сетевые диаграммы отображают сетевую модель конкретного проекта или плана действий на заданный период в виде множества вершин, которые соответствуют запланированным в рамках данного плана операциям и процедурам. Каждая вершина соединена с предшествующей и следующей вершинами логическими линиями, представляющими взаимосвязь между операциями. Исключение составляют начальная и финальная вершина, соответствующие первой и последней операции в рамках конкретного проекта или плана действий в заданном периоде.
Перед непосредственным построением сетевой диаграммы проводится работа по формированию операций в рамках конкретного проекта или плана действий на заданный период. Предварительно составляется формализованная структура операций в табличной форме.
Пример формализованной структуры операций
Задача о назначениях (зн).
Задача заключается в выборе такого распределения ресурсов по объектам, при котором минимизируется стоимость назначений.
Возможные применения задачи о назначениях:
Критерии эффективности
объем переработанной продукции
Матрица стоимостей С имеет вид , где — затраты, связанные с назначением i-го ресурса на j-й объект, , где n – число объектов или ресурсов.
Решение задачи может быть записано в виде .
Допустимое решение называется назначением. Оно строится путем выбора ровно одного элемента в каждой строке матрицы и ровно одно элемента в каждом столбце этой матрицы.
Э лементы матрицы С, соответствующие элементам матрицы Х, будем отмечать кружками: .
Математическая постановка задачи о назначениях: min при ограничениях , , .
Алгоритм решения задачи о назначениях.
Задача о назначениях является частным случаем транспортной задачи, в которой , поэтому ее можно решать алгоритмами ТЗ.
Рассмотрим другой метод, который является более эффективным, учитывающим специфику математической модели. Этот метод называется венгерским алгоритмом. Оно состоит из следующих шагов:
- преобразование строк и столбцов матрицы;
- определение назначения;
- модификация преобразованной матрицы.
1-й шаг: Цель данного шага – получение максимально возможного числа нулевых элементов в матрице С. для этого из всех элементов каждой строки вычитаем минимальный элемент соответствующей строки, а из всех элементов каждого столбца вычитаем минимальный элемент соответствующего столбца.
2-й шаг: Если после выполнения первого шага в каждой строке и каждом столбце матрицы С можно выбрать по одному нулевому элементу, то полученное решение будет оптимальным назначением.
3-й шаг: Если допустимое решение, состоящее из нулей, не найдено, то проводим минимальное число прямых через некоторые столбцы и строки так, чтобы все нули оказались вычеркнутыми. Выбираем наименьший невычеркнутый элемент. Этот элемент вычитаем из каждого невычеркнутого и прибавляем к каждому элементу, стоящему на пересечении проведенных прямых.
Если после проведения 3-го шага оптимальное решение не достигнуто, то процедуру проведения прямых следует повторять до тех пор, пока не будет получено оптимальное решение.
Пример. Фирма, имеющая 4 склада, получила 4 заказа, которые необходимо доставить различным потребителям. Складские помещения каждой базы имеют вполне достаточное количество, товара, чтобы выполнить любой один из этих заказов. Расстояние между базой и каждым потребителем приведены в матрице: . Как следует распределить заказы по базам, чтобы общая дальность транспортировки была минимальной?
1-й шаг: Значения минимальных элементов строк 1, 2, 3, 4 равны соответственно 2, 4, 11, 4. Вычитаем из элементов каждой строки соответствующее минимальное значение, получим: . Значения минимальных элементов столбцов 1, 2, 3, 4 равны соответственно 0, 0, 5, 0. Вычитаем из элементов каждого столбца соответствующее минимальное значение, получим: .
2—й шаг: Ни одно полное назначение не получено. Необходимо произвести модификацию матрицы стоимостей.
3 -й шаг: Вычеркиваем столбец 1, строку 3, строку 2 (или столбец 2): . Значение минимального невычеркнутого элемента равно 2. вычитаем его из всех невычеркнутых элементов и, складывая его со всеми элементами, расположенными на пересечении 2-х линий, получим: . Итак, . Ответ: первый заказ направляем на 3-ю базу, второй заказ – на 2-ю базу, третий заказ – на 4-ю базу, четвертый заказ – на 1-ю базу. Стоимость назначения: 9+4+11+4=28 ден. ед.