Сетевой график модель и его элементы

18. Назначение сетевых моделей и сетевых графиков классификация и элементы сетевых графиков

Основным методом решения плановых и управленческих задач в строительстве является метод сетевого планирования и управления (СПУ). Он включает построение, расчет, анализ и оптимизацию сетевых моделей и применяется для решения задач, связанных с планированием и управлением в строительстве.

Сетевой моделью называется ориентированный граф, отражающий последовательность и организационно-технологическую связь между ра­ботами.

Сетевые модели используются в строительстве для решения задач пер­спективного планирования, определения продолжительности и сроков выполнения основных этапов создания объектов, а также планирования капитальных вложений по периодам строительства.

Сетевая модель, представленная графически на плоскости с рассчи­танными временными и ресурсными параметрами называется сетевым графиком.

Сетевые модели классифицируются по следующим признакам: 1. По виду целей— одноцелевые (строительство одного объекта); многоцелевые (строительство организацией нескольких объектов).

2. По числу охвата объектов — частная модель; комплексная модель.

3. По характеру оценки параметров — детерминированная (с заранее и полностью обусловленными данными); вероятностная (с учетом слу­чайных факторов).

4. Модели с учетом целевой направленности— временные, ресурс­ные, стоимостные.

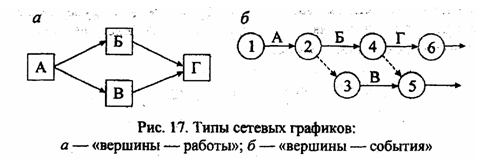
Сетевые графики бывают двух типов (рис. 17):

В дальнейшим мы будем работать с сетевыми графиками типа «вер­шины— события».

Элементы сетевого графика представлены в табл.

Таблица Элементы сетевого графика

Работа— производственный процесс, требующий затрат времени и ресурсов. На графике над стрелкой пишется наименование работы, под стрелкой — ее продолжительность (рис. 18, а).

Ожидание — процесс, требующий только затрат времени (выдержка бетона).

Зависимость — вводится в сетевой график для правильной взаимосвя­зи работ (рис. 18, б). Необходимость в ней диктуется технологией или ограничением материально-технических ресурсов.

Событие —- факт или момент окончания одной или нескольких работ, необходимый и достаточный для начала работ последующих.

Событие, не имеющее предшествующих работ, называется начальным, событие, не имеющее последующих работ, — конечным.

Путь— непрерывная последовательность работ (по направлению стрелок) от начального до конечного события. Путь наибольшей продол­жительности называется критическим и определяет срок строительства.

19. Правила построения сетевых графиков алгоритм расчета сетевого графика секторным методом. Оптимизация сетевых графиков

Прежде чем составлять сетевой график, следует определить, на сколь­ко захваток делится строящийся объект, и по возможности сохранить чис­ло и границы захваток по всем видам работ или делать их (в случае край­ней необходимости) кратными друг другу. В таблицу исходных данных вписывают работы по каждой захватке за исключением захваток, равных по трудоемкости и по объемам, тогда достаточно перечислить одну за­хватку, а ниже написать: «Вторая захватка — то же».

Составлять график следует по принципу: окончание каких работ должно послужить началом следующих.

Основные правила построения сетевых моделей следующие.

1. Нумерация событий производится слева направо и сверху вниз, но­мер присваивается событию, к которому не приходит ни одна стрелка из ранее не пронумерованного (пустого). При этом не должно быть повто­ряющихся номеров событий. Не допускается, чтобы разные работы (стрелки) имели одинаковый шифр.

2. В сетевом графике не допускается замкнутого контура работ, что легко выявляется, если соблюдать указанное выше правило нумерации.

Наличие замкнутых контуров свидетельствует об ошибке в построе­нии либо в составлении исходных данных.

3. Не должно быть тупиковых работ.

4. Зависимости (фиктивные работы) используются в графике для от­ражения взаимосвязей между работами.

5. При построении сетевого графика на строительство здания, имею­щего число захваток больше двух, события средних цепочек нужно рас­кладывать через холостую связь во избежание ложных зависимостей

Для работы А на третьей захватке необязательно окончание работы Б на первой и так далее, поэтому события средней цепочки следует разло­жить,

6. При составлении графика желательно иметь направление стрелок слева направо и избегать их пересечения.

Расчет ведется непосредственно на графике. Для этого каждое событие делится на четыре сектора, в которых указываются все необходимые для расчета данные о работе и событиях графика.

Сначала определяют ранние начала работ, которые записываются в ле­вом секторе четырехсекторного события. Ранние начала работ, выходя­щих из первого события, принимают равными нулю (ранние начала ис­ходных работ).

Раннее начало любой другой работы равно наибольшей из сумм ран­них начал и продолжительностей предшествующих работ, т. е. наиболь­шему раннему окончанию.

Таким образом, последовательно от исходного события до завершаю­щего определяются все ранние начала работ. Завершающее событие рас­сматривается как начальное событие условной работы с нулевой продол­жительностью.

Поздние окончания работ определяются справа налево, причем позд­нее окончание завершающих работ равно наибольшему из ранних их окончаний.

Позднее окончание любой работы сетевого графика равно наименьшей из разностей поздних окончаний последующих работ и их продолжительностей.

Все работы, входящие в одно событие, имеют одинаковые поздние окончания.

Разница значений правого и левого секторов дает нам величину общих резервов событий, которые записываются в знаменателе нижнего сектора. На этом заканчивается расчет графика.

Критический путь определяется по событиям, ранние и поздние сроки свершения которых (числа в правых и левых секторах) равны между со­бой.

Оптимизация сетевых графиков.

Для оптимизации сетевых графиков по ресурсам Имеются следующие алгоритмы:

1. Рациональное распределение ограниченных ресурсов.

2. Минимизация максимального потребления ресурсов в единицу времени.

3. Минимизация неравномерностей потребления ресурсов, т. е. лик­видация «пиков» и «провалов».

Все эти алгоритмы дают возможность сократить суммарное потребле­ние ресурсов в единицу времени без увеличения продолжительности критического пути сетевого графика. Наиболее эффективным по времени, затрачиваемому на расчеты, является алгоритм минимизации максималь­ного потребления ресурсов в единицу времени.

Алгоритм минимизации максимального потребления ресурсов, заключается в постепенном снижении максимального потребления ресурсов.

Источник

9. Параметры, элементы и правила построения сетевых моделей, расчет сетевого графика (показать на примере).

начала одной или нескольких последующих работ(Рис. 2.3.).

работа, производственный процесс, требующий затрат

Т – к – N рабочего времени, материальных ресурсов, затрат машинного времени.

— — — — — — — — — — — — — Технологическая зависимость — показывает зависимость начала выполнения каких либо последующих работ от окончания одной или нескольких предыдущих.

Позднее окончание работы (а),

Критический путь — это самый длинный путь (в днях) от исходного до завершающего события.

————————————————————————————————

Рис. 2.3. Схема обозначения основных элементов сетевой модели

Правила построения и расчета сетевой модели

1. Направление стрелок следует принимать слева направо
2. Форма модели и графика должна быть простой, без лишних пересечений, большинство работ следует изображать горизонтальными линиями
3. При выполнении параллельных работ, т.е. если одно событие служит началом двух работ или более, заканчивающихся другим событием, вводится зависимость и дополнительное событие, иначе разные работы будут иметь одинаковый код.
4. В графике не должно быть «тупиков», «хвостов» и «циклов». «Тупик» – событие (кроме завершающего), из которого не выходит ни одна работа. «Хвост» – событие (кроме исходного), в которое не входит ни одна работа. «Цикл» – замкнутый контур.
5. Разрабатываемая сетевая модель строительства должна отражать абсолютно достоверно все особенности объекта, для чего предварительно необходимо изучить и проанализировать всю проектно-сметную документацию по объекту.

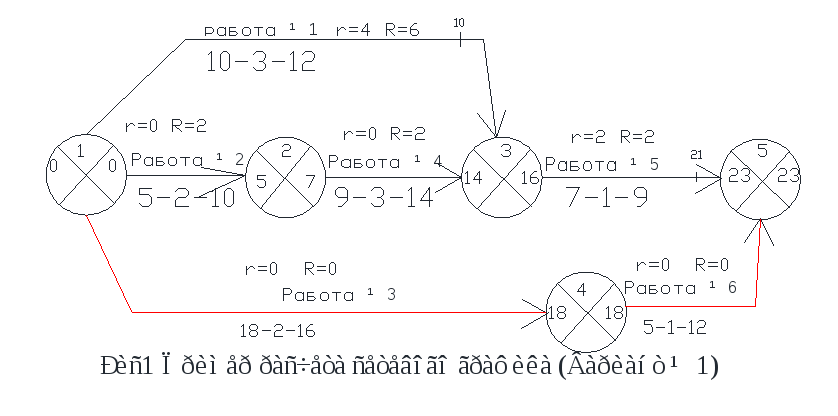
Сетевая модель и график могут разрабатываться в безразмерном (без масштабном) виде, то есть длина стрелок работ не соответствует значению продолжительности. Прежде чем приступать к расчету необходимо: -сетевую модель строительства объекта согласовать со всеми заинтересованными участниками строительства; -определить продолжительность выполнения каждой работы; -уточнить сроки строительства объекта по договору подряда. Параметры сетевого графика Параметры работ и сетевого графика: -номер события; -продолжительность выполнения работ; -раннее начало и раннее окончание работ; -позднее начало и позднее окончание работ; -частный резерв (запас) времени каждой работы; -общий резерв (запас) времени каждой работы; -длина критического пути (в днях) Расчет сетевого графика До начала выполнения расчета сетевого графика необходимо рассчитать продолжительность выполнения каждой работы сетевого графика. Расчет можно осуществлять графическим (секторным- непосредственно на графике) или табличным способом. Расчет графическим способом начинается с определения ранних сроков начала и окончания работ. Следующий шаг – расчет поздних сроков. Расчет поздних сроков осуществляется, начиная от последнего события. При правильном расчете поздних сроков в первом событии в левом и правом секторе должна быть цифра «0». Путь от первого события до последнего с наибольшим значением продолжительности и носит название «критический путь». Кроме этого следует учитывать то, что критический путь проходит через события, у которых в левом и правом секторе цифры одинаковые, а работы не имеют запасов времени. Критический путь – это самый длинный путь от исходного до завершающего события. Это и есть продолжительность строительства объекта. Работы, лежащие на критическом пути, называются критическими, другие работы являются не критическими и обладают запасами времени – частным и общим. На графиках критический путь выделяется двойной или просто более жирной линией. Возможность определения запасов времени по некритическим работам и использования их при корректировке графиков по различным критериям – это главное отличие и достоинство сетевого моделирования по сравнению с линейными графиками и циклограммами. Следующий шаг — расчет запасов времени – частного и общего. Частный резерв времени ( r) – это количество дней, на которое рассматриваемую работу можно растянуть или передвинуть без изменения ее продолжительности, не изменяя раннее начало последующей работы. Общий резерв времени (R) – это количество дней, на которое рассматриваемую работу можно растянуть или передвинуть без изменения ее продолжительности, не изменяя длины критического пути (продолжительности строительства объекта). Рассчитанный сетевой график приведен на рисунке После завершения расчетов необходимо построить график в масштабе времени и оценить его на предмет соответствия определенным критериям оптимальности.

Источник