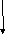Параметры сетевых моделей и методы их расчета
Сетевая модель имеет ряд характеристик, которые позволяют определить степень напряженности выполнения отдельных работ, а также всего их комплекса и принять решение о перераспределении ресурсов.
Ранний срок наступления события tр(i) — самый ранний из возможных сроков наступления события. Он равен продолжительности максимального пути от исходного события до данного.
tр(i) = max t[Lр(i)] (2.1)
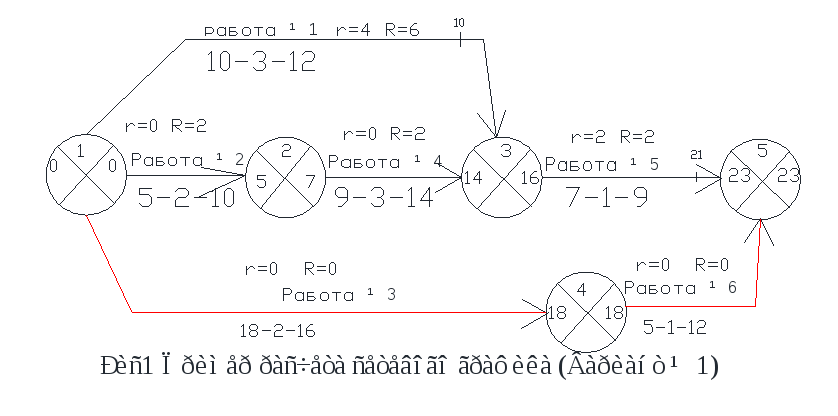
Например, tр(7)=19, т.к. L1=(1,2,4,7), L2=(1,3,4,7),
t(L1)=5+12=17 < t(L2)=7+12=19.
Ранний срок начала работы tр.н.(i,j) равен продолжительности максимального пути от исходного до начального события данной работы.
tр.н.(i,j)=max t[Ln(i)](2.2)
Например, tр.н.(7,11)=19, т.к. L1=(1,2,4,7), L2=(1,3,4,7),
t(L1)=5+12=17
Ранний срок начала работы равен раннему сроку наступления начального события данной работы.
tр.н.(i,j) = tр(i) (2.3)
Ранний срок окончания работы tр.о.( i,j) равен сумме раннего срока начала работы и продолжительности данной работы.
tр.о.(i,j)= tр.н.(i,j) + t(i,j) (2.4)
Например, tр.о.(7,11)= tр.н.(7,11) + t(7,11)= 19+8=27.
Поздний срок наступления события tп( i) равен разности между продолжительностью критического пути и продолжительностью максимального пути от данного события до завершающего.
tп(i) =Tкр — max t[Lк(i)](2.5)
Например, tп(7)=19, т.к. L1=(7,11), L2=(7,9,11), t(L1)=8 > t(L2)=4,
tп(7) = Tкр — max t[Lк(7)]=27 — 8=19.
Для событий критического пути tр( i)=tп(i), для других событий tр(i)tп(i).
Поздний срок окончания работы tп.о.( i,j) – это самый поздний срок окончания работы, при котором планируемый срок окончания проекта не меняется, он равен разности между продолжительностью критического пути и продолжительностью максимального пути от конечного события данной работы до завершающего события.
tп.о.(i,j)=Tкр — max t[Lк(j)] (2.6)
Поздний срок окончания работы равен позднему сроку наступления конечного события tп.о.(i,j) = tп(j). Например, tп.о.(4,7) = tп(7)=19.
Поздний срок начала работы tп.н.( i,j) – самый поздний срок начала работы, при котором планируемый срок окончания проекта не меняется.
tп.н.(i,j)= tп .о.(i,j) — t(i,j) (2.7)
Например, tп.н.(4,7)= tп.о.(4,7) — t(4,7)=19-12=7.
Для работ критического пути ранние и поздние сроки начала и окончания работ равны: tр.н.(4,7)= tп.н.(4,7)=7, tр.о.(4,7)= tп.о.(4,7)=19.
Работы, не лежащие на критическом пути, могут иметь резервы времени.
Полный резерв времени Rп( i,j) – максимальное время, на которое можно увеличить продолжительность данной работы, не изменяя продолжительности критического пути.
Rп (i,j)= tп(j) — tр(i) — t(i,j)
Rп(i,j)= tп.н (i,j) — tр.н.(i,j) (2.8)
Rп (i,j)= tп.о.(i,j) — tр.о.(i,j)
Свободный резерв времени Rс( i,j) равен разности между ранним началом последующей работы и ранним окончанием рассматриваемой работы.
Rс(i,j)= tр.н (j,к) — tр.о.(i,j) (2.9) Перейти к онлайн решению своей задачи
9. Параметры, элементы и правила построения сетевых моделей, расчет сетевого графика (показать на примере).
начала одной или нескольких последующих работ(Рис. 2.3.).

Т – к – N рабочего времени, материальных ресурсов, затрат машинного времени.
— — — — — — — — — — — — — Технологическая зависимость — показывает зависимость начала выполнения каких либо последующих работ от окончания одной или нескольких предыдущих.
Позднее окончание работы (а),

—
Рис. 2.3. Схема обозначения основных элементов сетевой модели
Правила построения и расчета сетевой модели
- Направление стрелок следует принимать слева направо
- Форма модели и графика должна быть простой, без лишних пересечений, большинство работ следует изображать горизонтальными линиями
- При выполнении параллельных работ, т.е. если одно событие служит началом двух работ или более, заканчивающихся другим событием, вводится зависимость и дополнительное событие, иначе разные работы будут иметь одинаковый код.
- В графике не должно быть «тупиков», «хвостов» и «циклов». «Тупик» – событие (кроме завершающего), из которого не выходит ни одна работа. «Хвост» – событие (кроме исходного), в которое не входит ни одна работа. «Цикл» – замкнутый контур.
- Разрабатываемая сетевая модель строительства должна отражать абсолютно достоверно все особенности объекта, для чего предварительно необходимо изучить и проанализировать всю проектно-сметную документацию по объекту.
Сетевая модель и график могут разрабатываться в безразмерном (без масштабном) виде, то есть длина стрелок работ не соответствует значению продолжительности. Прежде чем приступать к расчету необходимо: -сетевую модель строительства объекта согласовать со всеми заинтересованными участниками строительства; -определить продолжительность выполнения каждой работы; -уточнить сроки строительства объекта по договору подряда. Параметры сетевого графика Параметры работ и сетевого графика: -номер события; -продолжительность выполнения работ; -раннее начало и раннее окончание работ; -позднее начало и позднее окончание работ; -частный резерв (запас) времени каждой работы; -общий резерв (запас) времени каждой работы; -длина критического пути (в днях) Расчет сетевого графика До начала выполнения расчета сетевого графика необходимо рассчитать продолжительность выполнения каждой работы сетевого графика. Расчет можно осуществлять графическим (секторным- непосредственно на графике) или табличным способом. Расчет графическим способом начинается с определения ранних сроков начала и окончания работ. Следующий шаг – расчет поздних сроков. Расчет поздних сроков осуществляется, начиная от последнего события. При правильном расчете поздних сроков в первом событии в левом и правом секторе должна быть цифра «0». Путь от первого события до последнего с наибольшим значением продолжительности и носит название «критический путь». Кроме этого следует учитывать то, что критический путь проходит через события, у которых в левом и правом секторе цифры одинаковые, а работы не имеют запасов времени. Критический путь – это самый длинный путь от исходного до завершающего события. Это и есть продолжительность строительства объекта. Работы, лежащие на критическом пути, называются критическими, другие работы являются не критическими и обладают запасами времени – частным и общим. На графиках критический путь выделяется двойной или просто более жирной линией. Возможность определения запасов времени по некритическим работам и использования их при корректировке графиков по различным критериям – это главное отличие и достоинство сетевого моделирования по сравнению с линейными графиками и циклограммами. Следующий шаг — расчет запасов времени – частного и общего. Частный резерв времени ( r) – это количество дней, на которое рассматриваемую работу можно растянуть или передвинуть без изменения ее продолжительности, не изменяя раннее начало последующей работы. Общий резерв времени (R) – это количество дней, на которое рассматриваемую работу можно растянуть или передвинуть без изменения ее продолжительности, не изменяя длины критического пути (продолжительности строительства объекта). Рассчитанный сетевой график приведен на рисунке После завершения расчетов необходимо построить график в масштабе времени и оценить его на предмет соответствия определенным критериям оптимальности.
Графический метод расчета параметров сетевого графика
Рассчитать параметры сетевой модели графическим (секторным) методом можно через калькулятор.
Помимо него существуют следующие способы расчета: табличный метод, метод потенциалов.
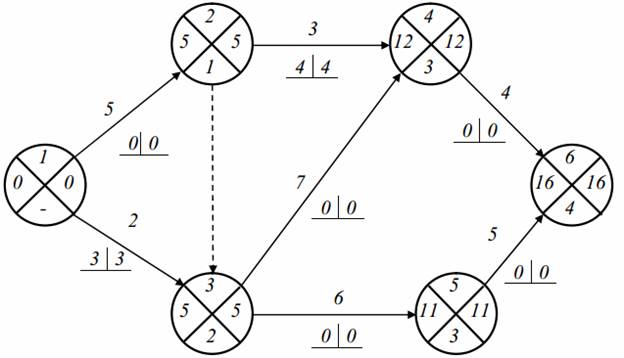
Пример . Определим параметры для событий и критический путь на графике. На практике получил широкое распространение четырехсекторный способ расчета ранних и поздних сроков свершения событий. При этом способе кружок сетевого графика, обозначающий событие, делится на четыре сектора (рис. 2, а). В верхнем ставится номер события i, в левом – наиболее раннее из возможных время свершения события tp(i), в правом – наиболее позднее из допустимых время свершения события tп(i), в нижнем – резерв времени данного события R(i).
Рисунок 2 — Графический способ расчета параметров: а) обозначения в вершине графика; б) сетевой график.
Раннее время свершения события tp(i) определяется продолжительностью максимального пути max(t) до (i), предшествующего событию i: tp(i)=max(t) до (i).
Послойно, переходя от исходного события до конечного, определим tp(i). Всегда для начального события tp(1)=0.
Для события 3 (рис., б) – tp(3)=max=5; для события 4 – tp(4)=max=11.
Длина критического пути Lкр=11. Послойно, переходя от конечного события до начального, определим tп(i). Всегда для конечного события tп(4)=t(Lкр)=11. Позднее время свершения события tп(i) определяется временем достаточным для выполнения работ, следующих за этим событием, т.е. зная продолжительность максимального из последующих за событием i путей max(t) после (i) и продолжительность критического пути t(Lкр), можно найти tп(i)= t(Lкр)-max(t) после (i).
Для события 2 – tп(3)=11-max=2.
Для критического пути время раннего свершения события tp(i) равно времени позднего свершения этого события tп(i), т.е. tp(i)= tп(i). Зная ранние и поздние сроки свершения событий сетевого графика, легко выявить резерв времени каждого из них R(i)= tп(i)- tp(i).
Резерв времени события показывает максимально допустимое время, на которое можно отодвинуть момент его свершения, не вызывая увеличения критического пути. События критического пути резерва времени не имеют.
Связь параметров сетевого графика для событий и работ показана в таблице.
Таблица — Расчет параметров работ
| Время | Начало i → j Окончание | |
| Раннее | tрн(ij)= tp(i) | tро(ij)= tp(i)+tij |
| Позднее | tпн(ij)= tп(j)-tij | tпо(ij)= tп(j) |
Резерв времени для работы R(ij) определяется по формуле: R(ij)= tп(j)- tр(i)-tij.