Практическое занятие 1
Как уже говорилось, для описания, анализа и оптимизации проектов очень удобным инструментом являются сетевые модели и в выполняемых лабораторных работах будут рассматриваться два основных представления сетевых моделей: сетевой график и временная диаграмма.
Рассмотрим практические примеры.
Напомним, что иногда роль вершин графа могут играть события, определяющие начало и окончание отдельных работ, а дуги в этом случае соответствуют работам. Графы такого типа называют “работа-дуга”, а соответствующую сетевую модель — сетевой моделью с работами на дугах (Activities on Arrows, AoA). Этот тип модели является устаревшим, часто обладает избыточностью (фиктивные работы) и в программных продуктах фактически не используется (хотя иногда еще встречается в отечественной литературе).
Когда в сетевой модели вершинами графа являются работы, а дуги отображают соответствие между окончанием одной работы и началом следующей, то графы такого типа называют “работа-вершина”, а соответствующую сетевую модель называют сетевой моделью с работами в узлах (Activities on Nodes, AoN). В Microsoft Project реализуется только этот тип модели, его и рассмотрим в практическом примере.
Выделяются следующие виды работ:
- простая
- событие (работа с нулевой длительностью, работа — веха)
- суммарная (состоящая из множества вложенных в нее работ любого вида)
Различают достаточно много временных параметров, но в примере будем рассматривать лишь те, которые непосредственно будут вычисляться в Microsoft Project. Это:
- продолжительность работы;
- раннее время начала работы;
- раннее время окончания работы;
- позднее время начала работы;
- позднее время окончания работы;
- общий резерв времени выполнения работы
Продолжительность работы – это календарное время, которое занимает выполнение работы. Любая последовательность непосредственно следующих друг за другом работ в сетевой модели называется путем. Путей в сетевой модели может быть много. Пути, связывающие исходное и завершающее события сетевой модели, называются полными, а все остальные – неполными. Сумма продолжительностей выполнения работ, составляющих тот или иной путь, называется продолжительностью этого пути. Самый продолжительный из всех полных путей называется критическим путем и, соответственно, продолжительность критического пути равна сумме продолжительностей всех работ, составляющих этот путь. Работы, критического пути, называются критическими работами, а события – критическими событиями. Понятие критического пути сетевой модели проекта является очень важным, так как на его основе строится метод организации управления всем комплексом работ – метод критического пути (Critical Path Method, CPM). Суть метода состоит в том, что именно продолжительность критического пути определяет длительность проекта, и, соответственно для сокращения длительности выполнения проекта необходимо сокращать длительность задач, лежащих на критическом пути (обычно распараллеливанием работ или назначением дополнительных трудовых ресурсов). Работы, лежащие на критическом пути не имеют резервов времени, у работ же, не находящихся на критическом пути, как правило, имеются резервы времени, позволяющие на некоторое время откладывать их выполнение, если это необходимо. Через понятие критического пути можно дать определения оставшихся временных параметров: Раннее время начала работыTрн – это самая ранняя дата, с которой возможно начать работу с учетом необходимости выполнения всех предыдущих работ с имеющимися у них временными ограничениями Раннее время окончания работыТро – это самая ранняя дата, с которой возможно окончание работы с учетом ее длительности и с учетом необходимости выполнения всех предыдущих работ с имеющимися у них временными ограничениями Позднее время начала работыТпн – это самая поздняя дата, с которой можно начать работу без изменения продолжительности критического пути и даты окончания проекта Позднее время окончания работыТпо – это самая поздняя дата, с которой можно завершить работу без изменения продолжительности критического пути и даты окончания проекта Полный (общий) резерв времени выполнения работыTпр – это интервал времени, в пределах которого приращение длительности рассматриваемой работы, не изменит даты окончания реализации проекта Рассмотрим пример расчета сетевой модели. Исходная информация для построения топологии сетевой модели и продолжительности работ дана в таблице ниже. Таблица 1. Исходная информация.
| Код работы | Наименование работы | Продолжительность работы |
| 1-2 A 1-4 B 2-4 C 4-6 D 1-5 E 5-4 F 5-7 G 2-3 H 3-6 I 7-6 J 3-8 K 6-8 L 7-8 M | Исследование внутреннего рынка Исследование зарубежного рынка Определение сегмента внутреннего рынка Определение политики освоения сегментов внутреннего и зарубежного рынков Исследование качества выпускаемого товара Разработка программы по адаптации товара на рынке Разработка рекламной политики по продвижению товара на рынке Разработка программы услуг по передвижению товара Выбор посредников Разработка политики оптовой и розничной торговли Разработка торговой марки и упаковки Определение ценовой политики Разработка программы сервисного обслуживания | 3 7 4 2 5 8 3 6 2 10 4 7 8 |
Данная сетевая модель отображает процесс маркетингового исследования фирмы, желающей выйти со своим товаром на рынок. Цель расчета – определить окончательный срок исследования и календарные даты наступления событий и сроков начала и окончания работ. Если рассматривать сетевую модель типа “работа-дуга”, она будет выглядеть следующим образом 
Рисунок 1. Сетевая модель типа «работа-дуга». Перерисуем сетевую модель в представлении “работы — вершины”, указывая рядом с обозначением ее длительность. 
Рисунок 2. Сетевая модель типа «работа-вершина». Ручной расчет временных параметров реализуется по шагам, а получаемые результаты удобно заносить в таблицу 1: ШАГ 1. Определение последовательности выполнения работ В первый столбец таблицы занесем перечень работ с указанием длительности каждой из них. Непосредственно предшествующие работы занесем во второй столбец, а непосредственно следующие работы – в третий столбец. ШАГ 2.Определение раннего времени начала и раннего времени окончания работ. Определение раннего времени начала и раннего окончания работ, т.е. заполнение столбцов (4) и (5) таблицы 1 должно осуществляться одновременно, т.к. время начала одних работ зависит от времени окончания других. Заполнение указанных столбцов осуществляется последовательно от начала сетевой модели к ее концу. При этом действуют следующие правила:
- Раннее время начала выполнения работы равно 0, если данной работе непосредственно не предшествует ни одна из работ сетевой модели, или равно максимальному раннему времени окончания среди всех непосредственно предшествующих ей работ
- Раннее время окончания рассматриваемой работы равно раннему времени ее начала (из столбца (4)) плюс продолжительность работы (из столбца (5)).
Продолжительность критического пути равна максимальному значению в столбце (5). Исходя из вышесказанного, первыми будут рассматриваться работы A, B, E, как не имеющие предшественников (заполняем для них соответствующие ячейки столбцов 4 и 5). За работой A идут работы C, H, для которых также заполняем соответствующие им ячейки столбцов 4 и 5, исходя из рассчитанного раннего времени окончания работы А и продолжительностей работ C, H За работой E идут работы F, G, для которых также заполняем соответствующие им ячейки столбцов 4 и 5, исходя из рассчитанного раннего времени окончания работы E и продолжительностей работ F, G Далее по сформулированным правилам рассчитываем последовательно параметры работ в следующей последовательности D, I, J, K, L, M, N и заполняем все ячейки столбцов 4 и 5 Продолжительность критического пути составляет 25 дней. Очевидно, что он состоит из работ E, G, J, L. Это означает, что все работы сетевой модели по маркетинговому исследованию могут быть выполнены не менее чем за 25 дней.
Правила построения сетевых графиков
Для построения сетевого графика необходимо выявить последовательность и взаимосвязь работ: какие работы необходимо выполнить, и какие условия обеспечить, чтобы можно было начать данную работу, какие работы можно и целесообразно выполнять параллельно с данной работой, какие работы можно начать после окончания данной работы. Эти вопросы позволяют выявить технологическую взаимосвязь между отдельными работами, обеспечивают логическое построение сетевого графика и его соответствие моделируемому комплексу работ.
Уровень детализации сетевого графика зависит от сложности строящегося объекта, количества используемых ресурсов, объёмов работ и продолжительности строительства.
Имеется два типа сетевых графиков:
Сетевые графики типа «вершины — работы».
Элементами такого графика являются работы и зависимости. Работа представляет собой определенный производственный процесс, требующий затрат времени и ресурсов для его выполнения, и изображается прямоугольником. Зависимость (фиктивная работа) показывает организационно-технологическую связь между работами, не требующую затрат времени и ресурсов, изображается стрелкой. Если между работами имеется организационный или технологический перерыв, то на зависимости указывается длительность этого перерыва. Пример сетевого графика «вершины — работы» приведен на рис. 6.1.
Рис. 6.1. Сетевой график типа «вершины — работы»
Если работа сетевого графика «вершины — работы» не имеет предшествующих работ, то она является исходной работой этого графика. Если работа не имеет последующих работ, то она является завершающей работой сетевого графика. В сетевом графике «вершины — работы» не должно быть замкнутых контуров (циклов), т.е. зависимости не должны возвращаться в ту работу, из которой они вышли.
Сетевые графики типа «вершины-события».
Элементами такого типа графиков являются работы, зависимости и события. Работа изображается сплошной стрелкой, зависимость – пунктирной. Событие представляет собой результат одной или нескольких работ, необходимый и достаточный для начала одной или нескольких последующих работ, и изображается кружком.
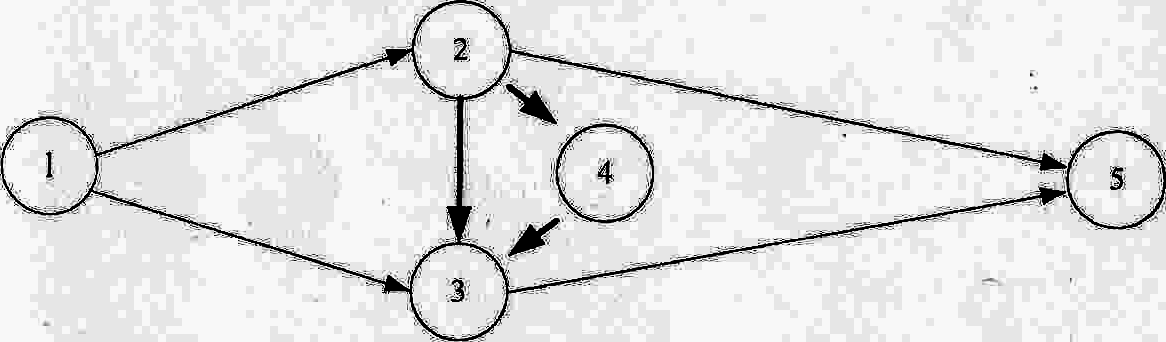
В сетевых графиках этого типа каждая работа находится между двумя событиями: начальным, из которого она выходит, и конечным, в которое она входит. События сетевого графика нумеруются, поэтому каждая работа имеет код, состоящий из номеров её начального и конечного события. Например, на рис. 6.2 работы закодированы как (1,2); (2,3); (2,4); (4,5).
Рис.6.2. Сетевой график «вершины — события»
Если событие сетевого графика «вершины-события» не имеет предшествующих работ, то оно является исходным событием этого графика. Следующие непосредственно за ним работы называются исходными. Если событие не имеет последующих работ, то оно является завершающим событием. Входящие в него работы называются завершающими.
Для правильного отображения взаимосвязей между работами необходимо соблюдать следующие основные правила построения сетевого графика «вершины-события»:
1. При изображении одновременно или параллельно выполняемых работ (например, работ «Б» и «В» на рис.6.2) вводятся зависимость (3,4) и дополнительное событие (3).
2. Если для начала работы «Г» необходимо выполнить работы «А» и «Б», а для начала работы «В» – только работу «А», то вводится зависимость и дополнительное событие (рис.6.3.).
Рис.6.3. Изображение зависимости между работами
3. В сетевом графике не д.б. замкнутых контуров (циклов), т.е. цепочки работ, возвращающейся к тому событию, из которого они вышли (рис.6.4).
Рис. 6.4. Пример замкнутого контура (2,4,3,2)
4. В сетевом графике при поточной организации строительства вводятся дополнительные события и зависимости (рис. 6.5.).
Рис. 6 5. Пример изображения потоков однородных работ