Составление сетевой модели на заданные циклы работ

Правила построения сетевых графиков

Для построения сетевого графика необходимо выявить последовательность и взаимосвязь работ: какие работы необходимо выполнить, и какие условия обеспечить, чтобы можно было начать данную работу, какие работы можно и целесообразно выполнять параллельно с данной работой, какие работы можно начать после окончания данной работы. Эти вопросы позволяют выявить технологическую взаимосвязь между отдельными работами, обеспечивают логическое построение сетевого графика и его соответствие моделируемому комплексу работ.

Уровень детализации сетевого графика зависит от сложности строящегося объекта, количества используемых ресурсов, объёмов работ и продолжительности строительства.

Имеется два типа сетевых графиков:

Сетевые графики типа «вершины — работы».

Элементами такого графика являются работы и зависимости. Работа представляет собой определенный производственный процесс, требующий затрат времени и ресурсов для его выполнения, и изображается прямоугольником. Зависимость (фиктивная работа) показывает организационно-технологическую связь между работами, не требующую затрат времени и ресурсов, изображается стрелкой. Если между рабо­тами имеется организационный или технологический перерыв, то на зависимости указывается длительность этого перерыва. Пример сетевого графика «вершины — работы» приведен на рис. 6.1.

Рис. 6.1. Сетевой график типа «вершины — работы»

Если работа сетевого графика «вершины — работы» не имеет предшествующих работ, то она является исходной работой этого графика. Если работа не имеет последующих работ, то она является завершающей работой сетевого графика. В сетевом графике «вершины — работы» не должно быть замкнутых контуров (циклов), т.е. зависимости не должны возвращаться в ту работу, из которой они вышли.

Сетевые графики типа «вершины-события».

Элементами такого типа графиков являются работы, зависимости и события. Работа изображается сплошной стрелкой, зависимость – пунктирной. Событие представляет собой результат одной или нескольких работ, необходимый и достаточный для начала одной или нескольких последующих работ, и изображается кружком.

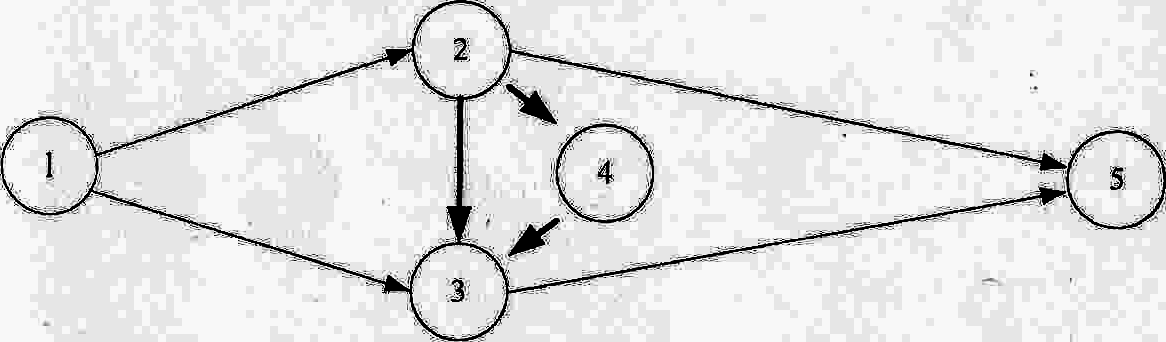
В сетевых графиках этого типа каждая работа находится между двумя событиями: начальным, из которого она выходит, и конечным, в которое она входит. События сетевого графика нумеруются, поэтому каждая работа имеет код, состоящий из номеров её начального и конечного события. Например, на рис. 6.2 работы закодированы как (1,2); (2,3); (2,4); (4,5).

Рис.6.2. Сетевой график «вершины — события»

Если событие сетевого графика «вершины-события» не имеет предшествующих работ, то оно является исходным событием этого графика. Следующие непосредственно за ним работы называются исходными. Если событие не имеет последующих работ, то оно является завершающим событием. Входящие в него работы называются завершающими.

Для правильного отображения взаимосвязей между работами необходимо соблюдать следующие основные правила построения сетевого графика «вершины-события»:

1. При изображении одновременно или параллельно выполняемых работ (например, работ «Б» и «В» на рис.6.2) вводятся зависимость (3,4) и дополнительное событие (3).

2. Если для начала работы «Г» необходимо выполнить работы «А» и «Б», а для начала работы «В» – только работу «А», то вводится зависимость и дополнительное событие (рис.6.3.).

Рис.6.3. Изображение зависимости между работами

3. В сетевом графике не д.б. замкнутых контуров (циклов), т.е. цепочки работ, возвращающейся к тому событию, из которого они вышли (рис.6.4).

Рис. 6.4. Пример замкнутого контура (2,4,3,2)

4. В сетевом графике при поточной организации строительства вводятся дополнительные события и зависимости (рис. 6.5.).

Рис. 6 5. Пример изображения потоков однородных работ

Источник

2. Правила построения сетевых моделей

В сетевой модели должна отражаться технологическая последовательность и очерёдность отдельных работ. Модель должна иметь простую форму. Стрелки должны быть направлены слева направо от события с меньшим номером к событию с большим номером, необходимо стремиться к минимальному пересечению отдельных работ.

2.1. Основные правила

1. Правило составных работ – любая работа а может быть разбита на составляющие, если после частичного выполнения её можно начать следующую работу б. При этом вводятся логические зависимости и дополнительные события (рис. 4).

2. Правило параллельных работ – если между двумя событиями необходимо показать две или несколько работ, которые выполняются параллельно, в модели вводятся дополнительное событие по окончании одной из параллельных работ и логическая зависимость (фиктивная работа) между ними (рис. 5).

3. Правило зависимых и независимых работ – если для начала одной работыг необходимо выполнение всех пред-шествующих работ a и б, а для начала работы в необходимо выполнение только работы a, то вводятся дополнительное событие и логическая зависимость (рис. 6).

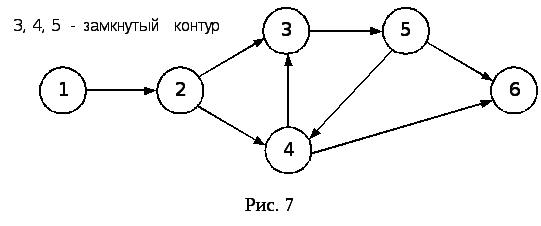
4. Правило запрещения замкнутых контуров, т.е. один путь не должен дважды проходить через одно событие (рис. 7).

5. Правило запрещения тупиковых событий, т.е. событий, из которых не выходит ни одна работа, если событие не завершающее (рис. 8).

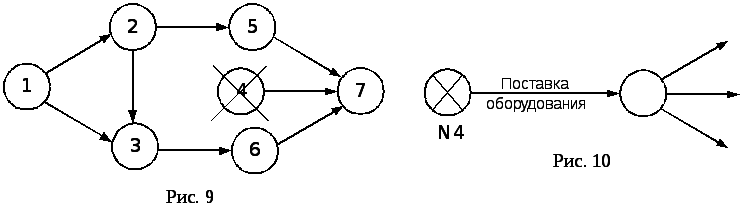
6. Правило запрещения необеспеченных событий, т.е. со- бытий, в которые не входит ни одна работа, если событие не исходное (рис. 9).

7. Правило изображения поставки (рис. 10).

2.2. Построение сетей

Для построения сетевой модели нужно знать технологию работ и зависимость одних работ от других. Последовательность выполнения работ записывается в форме таблицы, в которой указывается зависимость данной работы ig от предшествующей hi.

Пример 1. По данной зависимости работ построить сетевую модель.

Источник

2.2 Построение сетевой модели

На основании перечня работ и событий, последовательности работ и численности сотрудников построим сетевую модель (приложение А). По результатам модели срок выполнения ОКР – 604 дня, а директивный срок выполнения ОКР – 639 дней.

2.3. Оптимизация сетевого графика

Цель оптимизации состоит в максимально возможном сокращении длительности выполнения работ, т.е. в сокращении критического пути сетевого графика за счет перераспределения ресурсов (исполнителей) с некритических работ на критические, учитывая при этом категории исполнителей. Оптимизированный сетевой график приведен в приложении Б. Срок выполнения ОКР – 532 дня. В результате оптимизации срок выполнения ОКР сокращен на 72 дня.

2.4. Построение эпюры загрузки исполнителей

Минимизация потребности в одновременно необходимых исполнителях по категориям (конструкторы, технологи, техники-чертежники и т.д.) проводятся путем построения масштабного сетевого графика и эпюры загрузки (Приложение В).

2.5 Привязка сетевого графика к календарным срокам выполнения ОКР

Для выполнения этой работы за основу берется оптимизированный сетевой график, на который наносятся тонкие вертикальные линии, начиная с исходной и заканчивая завершающими событиями этапов. Результаты занесены в таблицу 2.2.

Таблица 2.2 – Привязка сетевого графика к календарю

1. Разработка технического задания

2. Разработка технического предложения

3. Эскизное проектирование

4. Разработка технического проекта

5. Разработка рабочей документации

6. Изготовление и испытание опытного образца

7. Доработка опытного образца и корректировка технической документации

2.6 Определение планового процента нарастания технической готовности ОКР

Опытно-конструкторские работы выполняются, как правило, в течении длительного календарного периода, поэтому на различных стадиях планирования, учета и анализа необходимо определить техническую готовность ОКР или отдельных ее этапов, которую принято выражать в процентах (Таблица 2.3 – Приложение Г)

3 Расчет затрат на опытно-конструкторскую разработку

В этом разделе рассчитаем затраты на Выполнение ОКР и составим смету по калькуляционным статьям. Смета затрат представлена в таблице 3.1.

В сметную стоимость ОКР включаются все прямые и косвенные затраты, связанные с ее выполнением, независимо то того, производится ли работа силами собственных сотрудников или оплачивается работа, выполненная на других пред­приятиях.

Для определения затрат на основную заработную плату необходимо знать нормативную трудоемкость выполнения ОКР (итоговые данные по таблице 1.4) и часовую ставку по каждой профессиональной группе исполнителей. Расчеты ве­дутся по формуле:

где З_окр – основная заработная плата производственного персонала по всей ОКР, р;

q – число профессиональных групп исполнителей

G_Чj – часовая тарифная ставка данной профессиональной группы, р;

T_j – нормативное время каждой профессиональной группы на выполнение своей работы по всей ОКР, н.-ч.

Расчет основной заработной платы производственного персонала:

Часовая ставка: 1000/176 =56,82 (р./час)

Заработная плата: 56,82*4684=266144,88 (р.)

Часовая ставка 8500/176 = 48,29 (р./час)

Заработная плата: 48,29*979 = 47275,91 (р.)

Часовая ставка- 9000/176 = 51,14 (р./час)

Заработная плата: 51,14*1386=70880,04 (р.)

Часа бая ставка: 9000/176 = 45,45 (р./час)

Заработная плата: 45,45*2817 = 128032,65 (р.)

Основная заработная плата производственного персонала:

266144,88+47275,91+70880,04+128032,65+134500,32 = 646 833,8 (р.)

Таблица 3.1 – Смета затрат на ОКР по статьям калькуляции

1. Материалы, покупные изделия и полуфабрикаты

2. Специальное оборудование для экспериментальных работ

3. Основная заработная плата производственного персонала

4. Дополнительная заработная плата

5. Отчисления на социальные нужды

7. Производственные командировки

8. Прочие производственные затраты

10. Итого затрат (себестоимость ОКР)

12. ВСЕГО: стоимость ОКР (цена научно-технической продукции)

4 Определение критической программы выпуска спроектированного изделия

Безубыточность работы предприятия во многом зависит от выбора оптимального объема производства и целесообразных темпов развития предприятия. Для анализа безубыточности необходимо уметь определить точку безубыточности предприятия. Под точкой безубыточности понимается такой объем продаж, при котором полученные доходы обеспечивают возмещение всех расходов, но не дают возможности получать прибыль. Иными словами, это нижний предел выпуска продукции, при котором прибыль равна нулю. Для определения этой точки нам понадобится себестоимость изделия (таблица 4.1).

Таблица 4.1 – Калькуляция себестоимости изделия

Источник