Принцип работы свёрточной нейронной сети. Просто о сложном
Глубокие нейронные сети привели к прорыву во множестве задач распознавания образов, таких как компьютерное зрение и распознавание голоса. Сверточная нейронная сеть один из популярных видов нейронных сетей.
В своей основе сверточную нейронную сеть можно рассматривать как нейронную сеть, использующую множество идентичных копий одного и того же нейрона. Это позволяет сети иметь ограниченное число параметров при вычислении больших моделей.
2D Свёрточная нейронная сеть
Этот приём с несколькими копиями одного и того же нейрона имеет близкую аналогию с абстракцией функций в математике и информатике. При программировании функция пишется один раз и затем повторно используется, не требуя писать один и тот же код множество раз в разных местах, что ускоряет выполнение программы и уменьшает количество ошибок. Аналогично сверточная нейронная сеть, однажды обучив нейрон, использует его во множестве мест, что облегчает обучение модели и минимизирует ошибки.
Структура сверточных нейронных сетей
Предположим, дана задача в которой требуется предсказать по аудио, есть ли голос человека в аудиофайле.
На входе получаем образцы аудио в разные моменты времени. Образцы равномерно распределены.
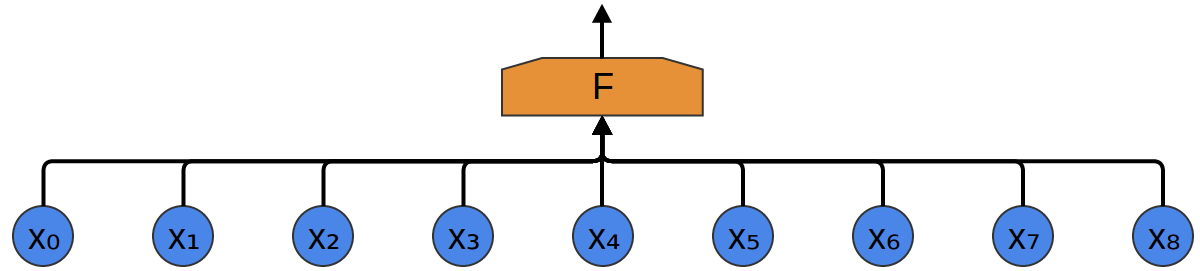
Самый простой способ классифицировать их с нейронной сетью — подключить все образцы к полносвязному слою. При этом каждый вход соединяется с каждым нейроном.
Более сложный подход учитывает некоторую симметрию в свойствах, которые которая находится в данных. Мы уделяем много внимания локальным свойствам данных: какая частота звука в течение определенного времени? Увеличивается или уменьшается? И так далее.
Мы учитываем те же свойства во все моменты времени. Полезно знать частоты вначале, середине и в конце. Обратите внимание, что это локальные свойства, поскольку нужно только небольшое окно аудиопоследовательности, чтобы определить их.
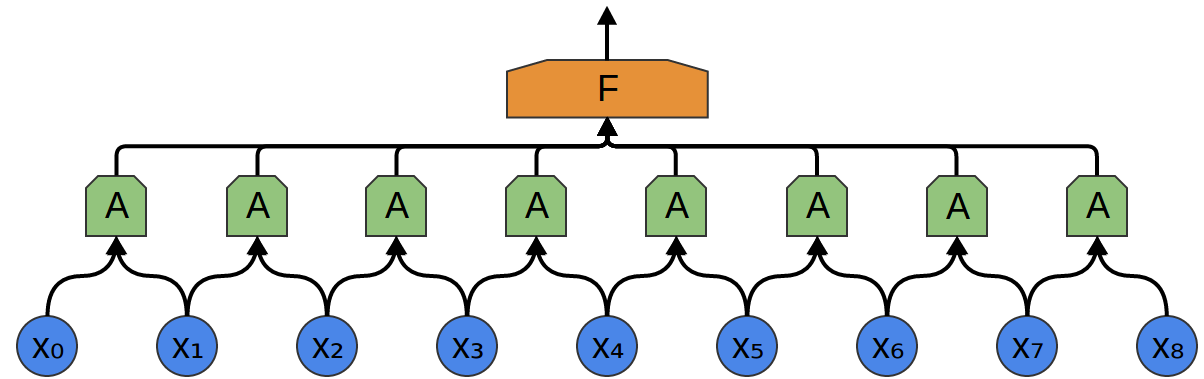
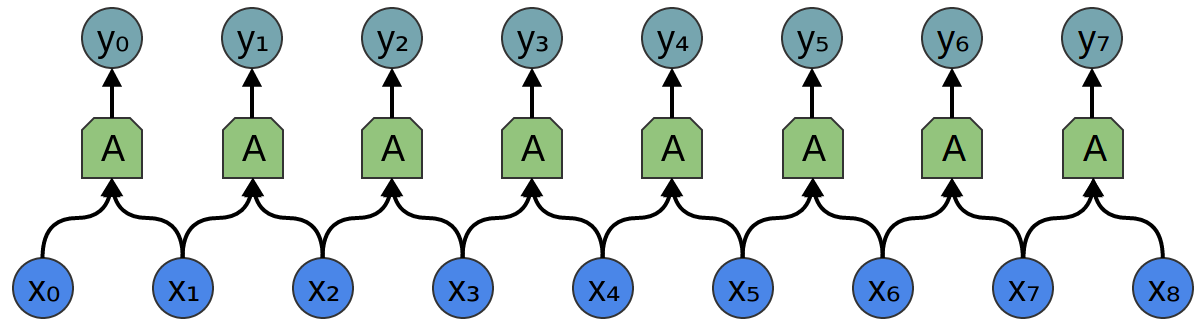
Таким образом, возможно создать группу нейронов A, которые рассматривают небольшие сегменты времени в наших данных. A смотрит на все такие сегменты, вычисляя определенные функции. Затем, выход этого сверточного слоя подается в полносвязный слой F.
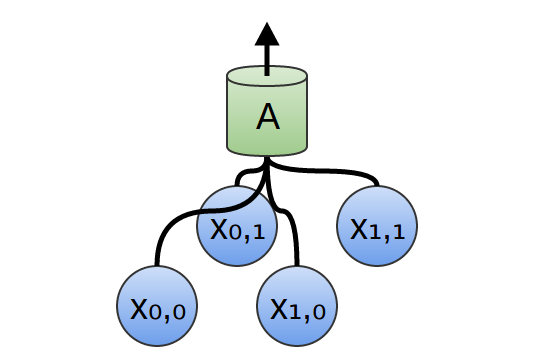
В приведенном выше примере A обрабатывало только сегменты, состоящие из двух точек. Это редко встречается на практике. Обычно, окно слоя свертки намного больше.
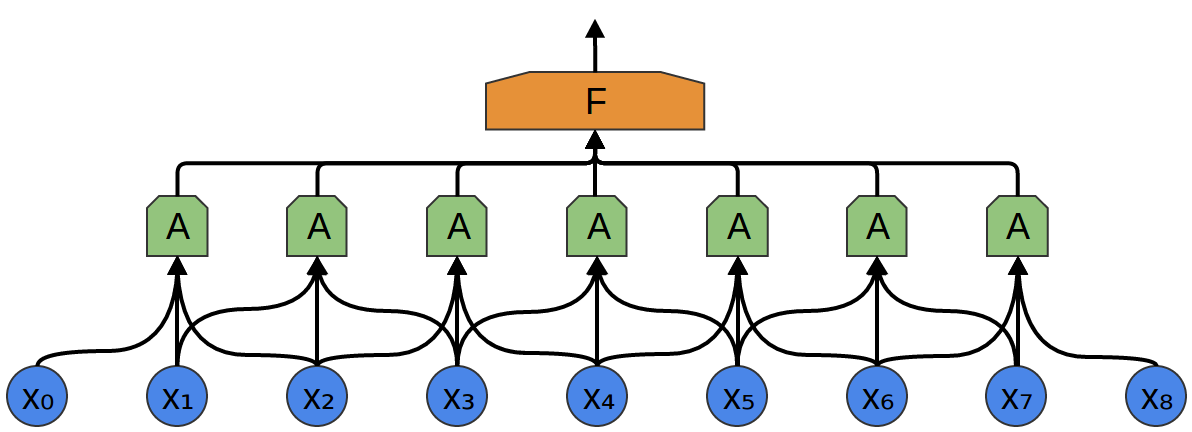
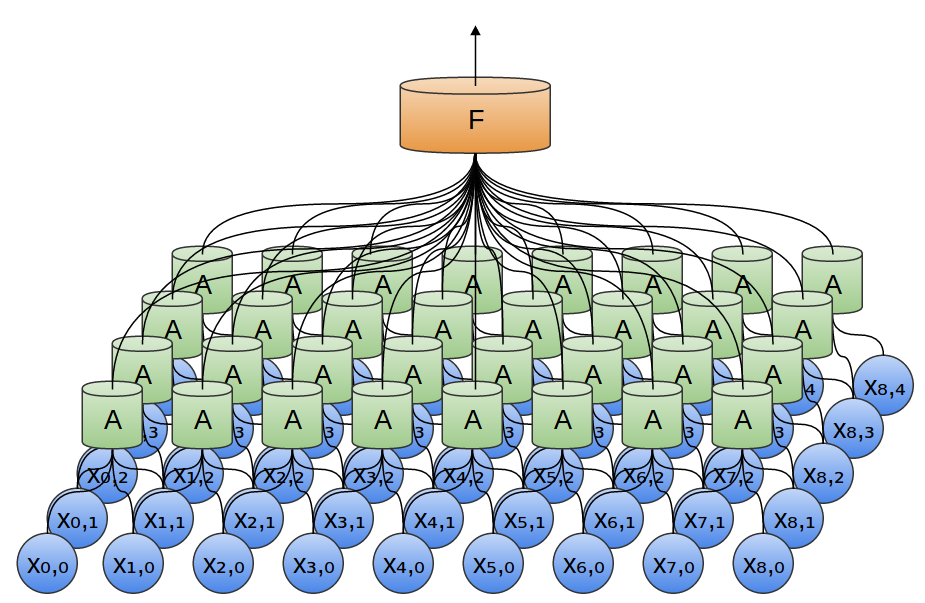
В следующем примере A получает на вход 3 отрезка. Это тоже маловероятно для реальных задач, но, к сожалению, сложно визуализировать A, соединяющее множество входов.
Одно приятное свойство сверточных слоев состоит в том, что они являются составными. Можно подавать вывод одного сверточного слоя в другой. С каждым слоем сеть обнаруживает более высокие, более абстрактные функции.
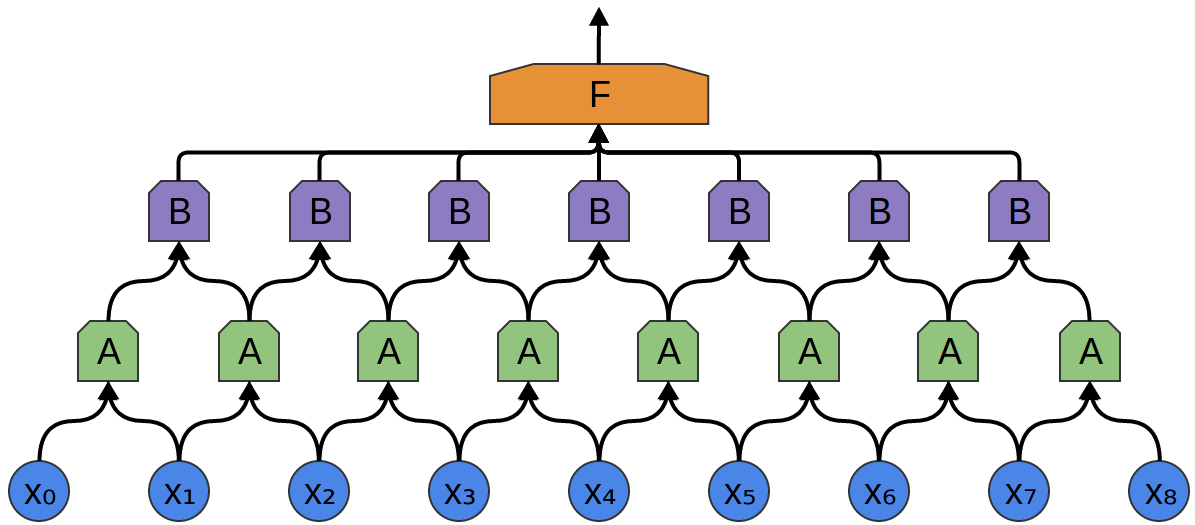
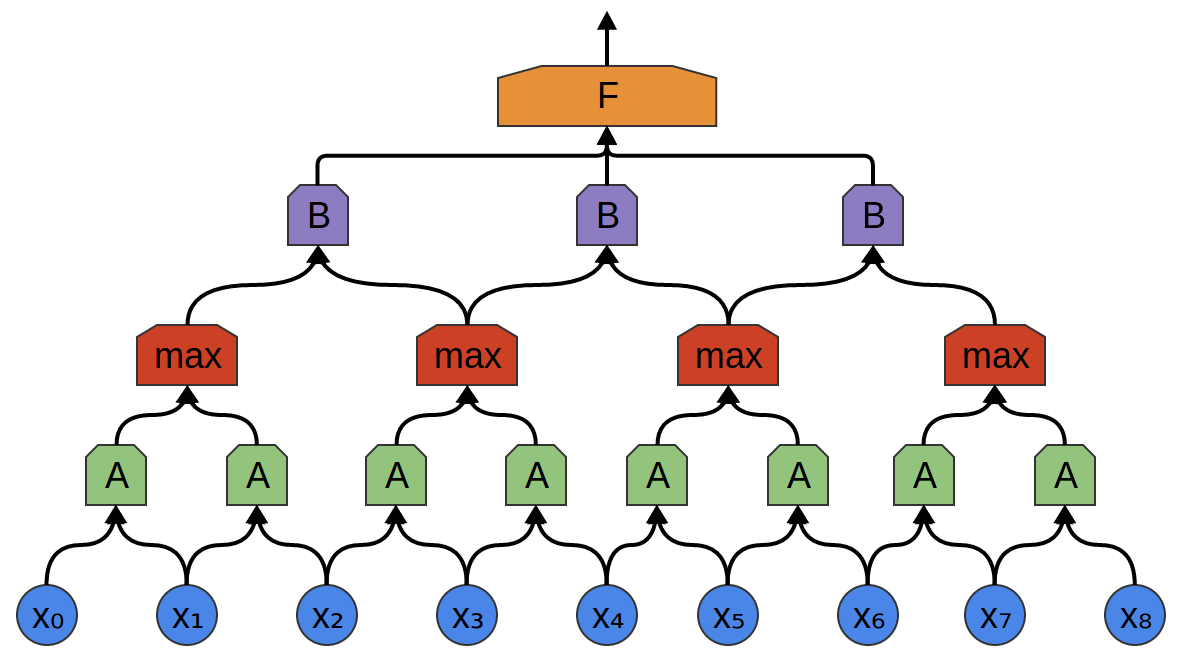
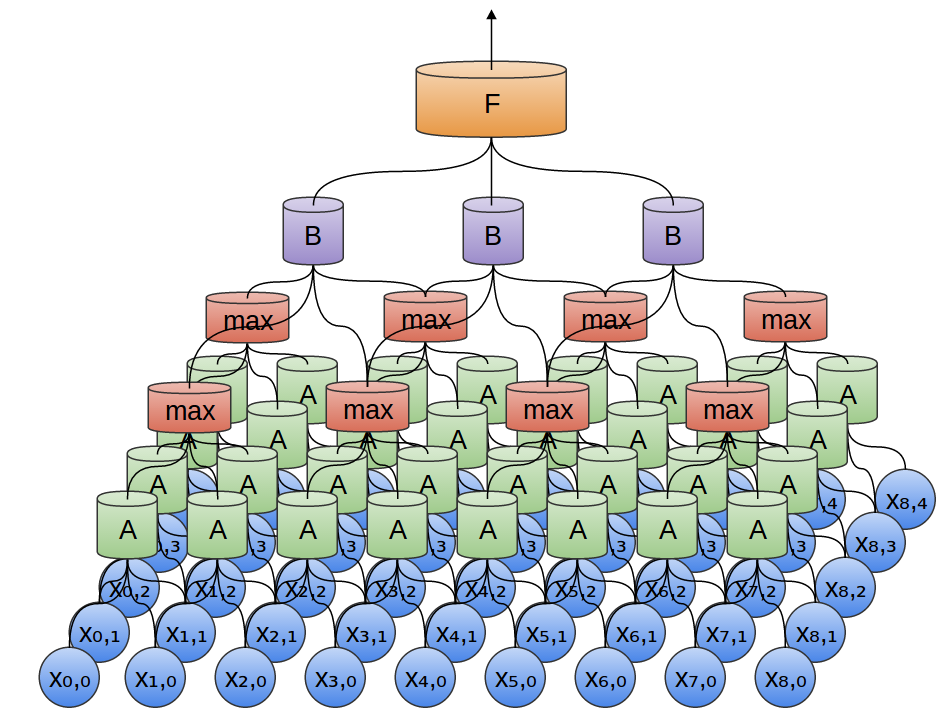
В следующем примере есть новая группа нейронов B. B используется для создания еще одного сверточного слоя, уложенного поверх предыдущего.
Сверточные слои часто переплетены pooling (объединяющими) слоями. В частности, есть вид слоя, называемый max-pooling, который чрезвычайно популярен.
Часто, нас не волнует точный момент времени, когда присутствует полезный сигнал в данных. Если изменение частоты сигнала происходит раньше или позже, имеет ли это значение?
Max-pooling вбирает максимум фичей из небольших блоков предыдущего уровня. Вывод говорит, присутствовал ли полезный сигнал функции в предыдущем слое, но не точно где.
Max-pooling слоев — это «уменьшение». Оно позволяют более поздним сверточным слоям работать на больших участках данных, потому что небольшие патчи после слоя объединения соответствует гораздо большему патчу перед ним. Они также делают нас инвариантными к некоторым очень небольшим преобразованиям данных.
В наших предыдущих примерах использовались одномерные сверточные слои. Однако сверточные слои могут работать и с более объемными данными. Фактически самые известные решения на базе сверточных нейронных сетей используют двумерные сверточные нейронные сети для распознавания образов.
В двумерном сверточном слое вместо того, чтобы смотреть на сегменты, A будет смотреть патчи.
Для каждого патча, A будет вычислять функции. Например, она может научиться обнаруживать наличие края, или текстуру, или контраст между двумя цветами.
В предыдущем примере вывод сверточного слоя подавался в полносвязный слой. Но, возможно составить два сверточных слоя, как это было в рассмотренном одномерном случае.
Мы, также можем выполнять max-pooling в двух измерениях. Здесь мы берем максимум фичей из небольшого патча.
Это сводится к тому, что при рассмотрении целого изображения не важно точное положение края, вплоть до пикселя. Достаточно знать, где он находится в пределах нескольких пикселей.
Также, иногда используются трехмерные сверточные сети для таких данных, таких как видео или объемные данные (например, 3D-сканирование в медицине). Однако, такие сети не очень широко используются, и гораздо сложнее в визуализации.
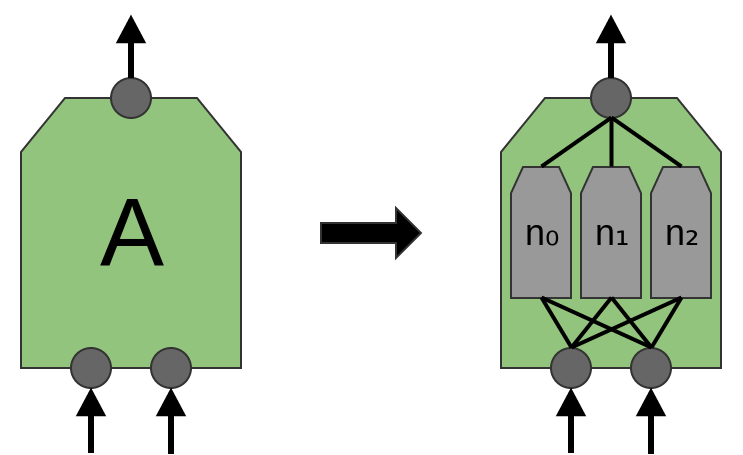
Ранее, мы говорили, что A — группа нейронов. Будем более точными в том: что такое А?
В традиционных сверточных слоях A представляет собой параллельную связку нейронов, все нейроны получают одинаковые входные сигналы и вычисляют разные функции.
Например, в двумерном сверточном слое один нейрон может обнаруживать горизонтальные края, другой, вертикальные края, а третий зелено-красные цветовые контрасты.
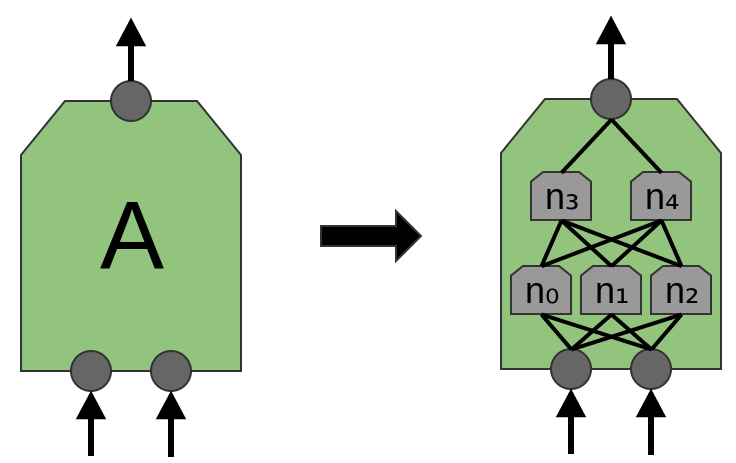
В статье ‘Network in Network’ (Lin et al. (2013)) предлагается новый слой «Mlpconv». В этой модели, A имеет несколько уровней нейронов, причем последний слой выводит функции более высокого уровня для обрабатываемого региона. В статье, модель достигает впечатляющих результатов, устанавливая новый уровень техники в ряде эталонных наборов данных.
Для целей этой публикации мы сосредоточимся на стандартных сверточных слоях.
Результаты сверточных нейронных сетей
В 2012 году Alex Krizhevsky, Ilya Sutskever, и Geoff Hinton достигли существенного улучшения качества распознавания в сравнении с известными на тот момент решениями (Krizehvsky et al. (2012)).
Прогресс был результатом объединения нескольких подходов. Использовались графические процессоры для обучения большой (по меркам 2012 года), глубокой нейронной сети. Использовался новый тип нейронов (ReLU) и новая техника для уменьшения проблемы, называемой «overfitting» (DropOut). Использовали большой набор данных с большим количеством категорий изображений (ImageNet). И конечно же, это была сверточная нейронная сеть.
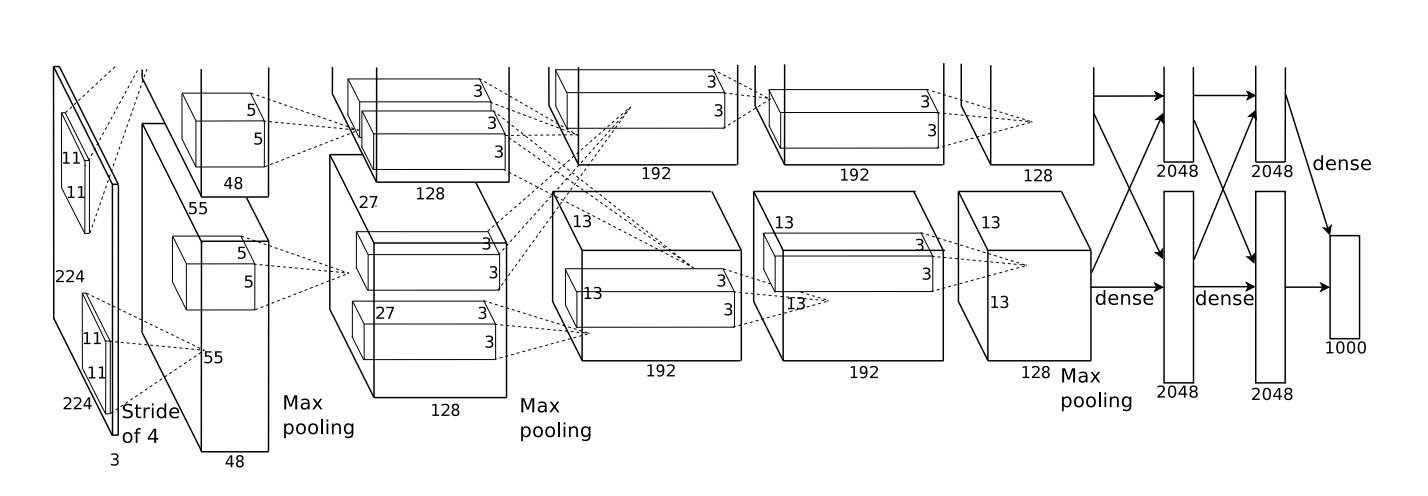
Архитектура, показанная ниже, была глубокой. Она имеет 5 сверточных слоев, 3 pooling с чередованием и три полносвязных слоя.
From Krizehvsky et al. (2012)
Сеть была обучена классификации фотографий в тысячи разных категорий.
Модель Крижевского и др. была способна дать правильный ответ в 63% случаев. Кроме того, правильный ответ из 5 лучших ответов, присутствует 85% прогнозов!
Проиллюстрируем, что узнает первый уровень сети.
Напомним, что сверточные слои были разделены между двумя графическими процессорами. Информация не идет назад и вперед по каждому слою. Оказывается, каждый раз, когда модель запускается, обе стороны специализируются.
Фильтры, полученные первым сверточным слоем. Верхняя половина соответствует слою на одном графическом процессоре, нижняя — на другом. From Krizehvsky et al. (2012)
Нейроны с одной сторону, фокусируются на черно-белом цвете, учась обнаруживать края разных ориентаций и размеров. Нейроны с другой стороны, специализируются на цвете и текстуре, обнаруживают цветовые контрасты и узоры. Помните, что нейроны случайным образом инициализируются. Ни один человек не пошел и не поставил их пограничными детекторами, или разделил таким образом. Это произошло при обучении сети классификации изображений.
Эти замечательные результаты (и другие захватывающие результаты примерно в то время) были только началом. За ними быстро последовало множество других работ, которые тестировали измененные подходы и постепенно улучшали результаты или применяли их в других областях.
Сверточные нейронные сети являются важным инструментом в компьютерном видении и современном распознавании образов.
Формализация сверточных нейронных сетей
Рассмотрим одномерный сверточный слой с входами и выводами :
Сравнительно легко описать результаты в терминах входных данных:
Например, в приведенном выше примере:
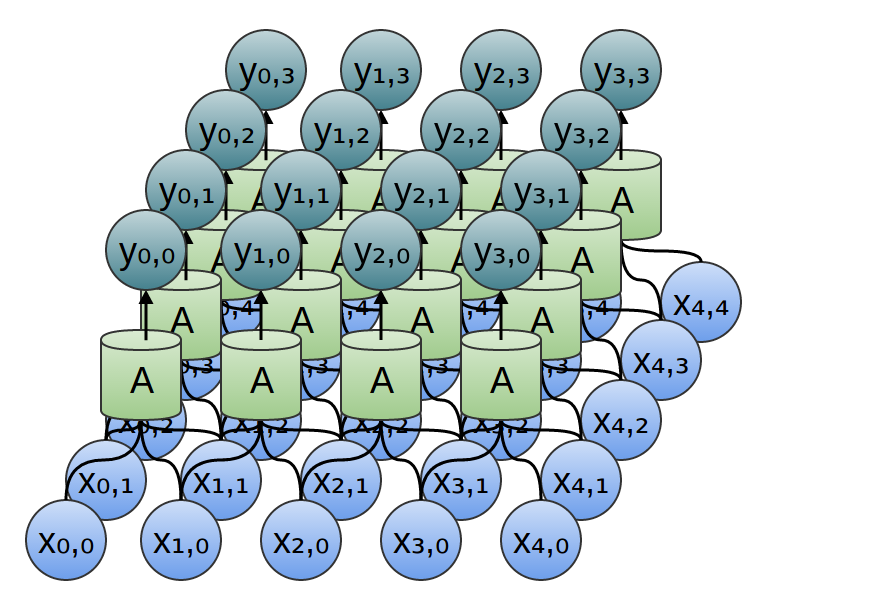
Аналогично, если мы рассмотрим двумерный сверточный слой с входами и выводами :
Сеть можно представить двумерной матрицей из значений.
Заключение
Операция свертки является мощным инструментом. В математике операция свёртки возникает в разных контекстах начиная от изучения уравнений с частными производными и заканчивая теорией вероятностей. Отчасти из-за своей роли в PDE, свертка важна в физических науках. Свёртка также играет важную роль во многих прикладных областях, таких как компьютерная графика и обработка сигналов.